198
)sin,sin,()( ,, τσ+τσ+=τ τ−τ−
21
0104652 5101350eeR . (9.2.5)
Theo c«ng thøc (3.2.12) mËt ®é phæ t−¬ng øng )(
ω
S ®· ®−îc x¸c ®Þnh d−íi d¹ng
×
σ−α−ωσ−α+ωσ−α−ω
−ω−ω
=ω ])(][)(][)([
),(),(
)( 2
21
22
11
22
11
2
2222 83486160
iii
S
)]()([ 2
2
22
21
2
1
α+ωα−α+ω
×i, (9.2.6)
trong ®ã .,;, 4652 010 21 =α=α
Sau ®ã, theo ph−¬ng ph¸p ®−îc tr×nh bμy trong môc 5.5 ®· t×m hμm truyÒn tèi −u
theo c«ng thøc (5.5.19), vμ tiÕp theo lμ t×m c«ng thøc ngo¹i suy tuyÕn tÝnh tèi −u biÓu thÞ
gi¸ trÞ dù b¸o cña ®¹i l−îng cÇn t×m t¹i thêi ®iÓm Tt + qua gi¸ trÞ cña nã vμ gi¸ trÞ cña
®¹o hμm c¸c bËc cña nã t¹i thêi ®iÓm t.
NÕu chØ giíi h¹n ë hai ®¹o hμm ®Çu tiªn, th× nhËn ®−îc nh÷ng c«ng thøc ngo¹i suy
tuyÕn tÝnh tèi −u gÇn ®óng chØ sè hoμn l−u vÜ h−íng víi thêi h¹n dù b¸o mét vμ hai
th¸ng d−íi d¹ng
)(,)(,)(,)( tJtJtJtJ ′′
−
′
+=+ 8143000270067301 , (9.2.7)
)(,)(,)(,)( tJtJtJtJ ′′
−
′
+=+ 0690000020005702 . (9.2.8)
Khi tÝnh c¸c ®¹o hμm ®· sö dông c¸c c«ng thøc néi suy Newton:
),()( 1−−=Δ≈
′tJtJJJ
).()()( 212
2−+−−=Δ≈
′′ tJtJtJJJ (9.2.9)
KÕt qu¶ dù b¸o J víi thêi h¹n dù b¸o mét th¸ng theo c«ng thøc (9.2.7) kh¸ phï hîp
víi c¸c gi¸ trÞ thùc. Dù b¸o ®¹i l−îng )( 2+tJ kh«ng cho kÕt qu¶ kh¶ quan.
Ch−¬ng 10: Mét sè vÊn ®Ò m« t¶ tr−êng tèc ®é giã
10.1. Hμm t−¬ng quan cña tèc ®é giã
Trong ch−¬ng 4 ®· chØ ra r»ng ®Ó x¸c ®Þnh kú väng to¸n häc vμ hμm t−¬ng quan cña
biÕn ®æi tuyÕn tÝnh hμm ngÉu nhiªn dõng nμo ®ã chØ cÇn biÕt kú väng to¸n häc vμ hμm t−¬ng
quan cña hμm ngÉu nhiªn ®−îc biÕn ®æi. Nh−ng trong thùc tiÔn th−êng x¶y ra c¸c tr−êng hîp
khi mèi liªn hÖ gi÷a c¸c hμm ngÉu nhiªn thùc sù kh«ng tuyÕn tÝnh. Khi ®ã ®Ó nhËn ®−îc c¸c
®Æc tr−ng cña hμm ngÉu nhiªn lμ kÕt qu¶ cña phÐp biÕn ®æi phi tuyÕn, th× biÕt kú väng to¸n
häc vμ hμm t−¬ng quan cña hμm ngÉu nhiªn ®−îc biÕn ®æi lμ ch−a ®ñ, mμ cÇn biÕt c¸c
m«men bËc cao hoÆc c¸c hμm ph©n bè nhiÒu chiÒu cña nã. Tuy nhiªn trong nhiÒu tr−êng hîp,
b»ng c¸ch sö dông nh÷ng thñ thuËt nh©n t¹o cã thÓ biÓu diÔn gÇn ®óng kú väng to¸n häc vμ
hμm t−¬ng quan cña kÕt qu¶ biÕn ®æi phi tuyÕn qua nh÷ng ®Æc tr−ng t−¬ng øng cña hμm
ngÉu nhiªn ®−îc biÕn ®æi.
§Ó lμm vÝ dô cho biÕn ®æi phi tuyÕn qu¸ tr×nh ngÉu nhiªn dõng, ta xÐt ph−¬ng ph¸p
gÇn ®óng x¸c ®Þnh hμm t−¬ng quan cña modul vËn tèc giã, nÕu biÕt tr−íc kú väng to¸n häc
vμ hμm t−¬ng quan cña c¸c thμnh phÇn cña vect¬ nμy. Th«ng th−êng vect¬ giã ®−îc xem nh−
199
vect¬ ngÉu nhiªn hai chiÒu, mμ c¸c thμnh phÇn )(tUx vμ )(tU y cña nã lμ nh÷ng hμm ngÉu
nhiªn kh«ng ®éc lËp víi nhau, t¹i mçi gi¸ trÞ
t
chóng tu©n theo qui luËt ph©n bè chuÈn cã
ph−¬ng sai b»ng nhau.
Cã thÓ x¸c ®Þnh ®−îc hμm t−¬ng quan cña modul vect¬ giã, nÕu biÕt quy luËt ph©n bè
hai chiÒu ),( 21 uuf , tøc mËt ®é ph©n bè ®ång thêi c¸c tèc ®é giã 1
U vμ 2
U lÊy ë nh÷ng thêi
®iÓm kh¸c nhau hay t¹i nh÷ng ®iÓm kh¸c nhau trong kh«ng gian. Ph−¬ng ph¸p nμy ®−îc A.
S. Martrenko xem xÐt trong c«ng tr×nh [60], ë ®ã trªn c¬ së x¸c ®Þnh lý thuyÕt mËt ®é ph©n bè
®ång thêi cña c¸c modul )( 1
Ut
vμ )( 2
Ut
, x¸c lËp mèi liªn hÖ gi÷a c¸c hμm t−¬ng quan cña
tr−êng vect¬ )(tU
vμ tr−êng v« h−íng )(tU
. Víi mét sè gi¶ thiÕt nμo ®ã ®· nhËn ®−îc nh÷ng
c«ng thøc t−¬ng ®èi ®¬n gi¶n, vμ thùc tÕ øng dông ®−îc, ®Ó tÝnh c¸c hÖ sè t−¬ng quan cho
tr−êng hîp tèc ®é giã trung b×nh gÇn b»ng kh«ng. Nh−ng thùc ra, nh− ®· nªu trong c«ng
tr×nh [60], trong nhiÒu tr−êng hîp tèc ®é giã trung b×nh mUM =
][ kh¸c kh«ng, vμ gi¸ trÞ cña
chóng cã thÓ v−ît qu¸ ph−¬ng sai 2
σ mét c¸ch ®¸ng kÓ. VÝ dô, trong c¸c ®iÒu kiÖn ®iÓn h×nh
®èi víi dßng ch¶y xiÕt th× ., 1242
2
2
÷=
σ
m BiÓu thøc ®èi víi mËt ®é ph©n bè ®ång thêi cña tèc ®é,
nhËn ®−îc trong c¸c ®iÒu kiÖn ®ã, rÊt cång kÒnh vμ trªn thùc tÕt kh«ng cho phÐp nhËn ®−îc
nh÷ng c«ng thøc kh¶ dÜ ®Ó tÝnh c¸c hÖ sè t−¬ng quan.
Chóng ta sÏ x©y dùng c¸c c«ng thøc ®Ó x¸c ®Þnh hμm t−¬ng quan tèc ®é giã cho tr−êng
hîp gi¸ trÞ trung b×nh cña tèc ®é giã lín h¬n ®¸ng kÓ so víi ®é lÖch b×nh ph−¬ng trung b×nh
cña chóng. Ph−¬ng ph¸p nμy dùa trªn c¬ së sö dông hμm ®Æc tr−ng cña hÖ c¸c ®¹i l−îng
ngÉu nhiªn cã d¹ng ®¬n gi¶n ®èi víi tr−êng hîp c¸c ®¹i l−îng ngÉu nhiªn ph©n bè chuÈn.
Bμi to¸n ®−îc ph¸t biÓu nh− sau. XÐt vect¬ ngÉu nhiªn hai chiÒu
jiU )()()( tUtUt yx += (10.1.1)
mμ c¸c thμnh phÇn )(tUx vμ )(tUy cña nã lμ nh÷ng hμm ngÉu nhiªn dõng ph©n bè chuÈn
cã kú väng to¸n häc x
m vμ y
m, c¸c ph−¬ng sai 2
σ== yx DD vμ c¸c hμm t−¬ng quan )(τ
x
R
vμ )(τ
y
R.
C¸c thμnh phÇn cña vect¬ ®−îc coi lμ kh«ng phô thuéc lÉn nhau, tøc hμm t−¬ng
quan quan hÖ cña chóng b»ng kh«ng.
Yªu cÇu x¸c ®Þnh hμm t−¬ng quan )(τ
u
R cña modul vect¬ ngÉu nhiªn
)()()( tUtUtU yx
22 += . (10.1.2)
Muèn vËy, ®Çu tiªn ta x¸c ®Þnh hμm t−¬ng quan cña b×nh ph−¬ng modul
)()()( tUtUtZ yx
22 += . (10.1.3)
HiÓn nhiªn hμm ngÉu nhiªn )(tZ kh«ng ph©n bè chuÈn, tuy vËy tÝnh dõng cña nã
®−îc gi÷ nguyªn.
Ta x¸c ®Þnh hμm t−¬ng quan )(τ
z
R
{}
=−τ+=−τ+−=τ 2
zzzz mtZtZMmtZmtZMR )]()([])(][)([)(
+τ++τ+= )]()([)]()([ tUtUMtUtUM yxxx
2222
22222
zyyxy mtUtUMtUtUM −τ++τ++ )]()([)]()([ , (10.1.4)
trong ®ã
200
222222222 2yxyxyxz mmmmUMUMm ++σ=+σ++σ=+= )()(][][ . (10.1.5)
Ta xÐt hÖ bèn ®¹i l−îng ngÉu nhiªn ph©n bè chuÈn
)(),(),(),( τ+==τ+== tUUtUUtUUtUU yyxx 4321 .
Hμm ®Æc tr−ng cña hÖ nμy, nh− ®· biÕt (xem môc 1.12), cã d¹ng
,exp),,,(
,
,
+−=
==
4
1
4
1
4321 2
1
kkkjk
jk jk umiuuRuuuuE (10.1.6)
trong ®ã k
m lμ c¸c kú väng to¸n häc cña c¸c ®¹i l−îng ngÉu nhiªn k
U, jk
R, lμ m«men
quan hÖ cña c¸c ®¹i l−îng ngÉu nhiªn k
U vμ j
U, chóng lμ nh÷ng phÇn tö cña ma trËn
t−¬ng quan jk
R,
)].)([(
,jjkkjk mUmUMR −−=
§èi víi hÖ c¸c ®¹i l−îng ngÉu nhiªn ®ang xÐt ta cã:
2
44332211 σ==== RRRR ;
)(),( τ=τ= yx RRRR 3412 ;
yx mmmmmm ==== 4321 ,. (10.1.7)
V× c¸c hμm ngÉu nhiªn )(tUx vμ )(tUy kh«ng phô thuéc lÉn nhau, nªn
.0
24142313 ==== RRRR
Nh− vËy ma trËn t−¬ng quan cã d¹ng
σ
τσ
σ
τσ
=
2
2
2
2
00
00
)(
)(
,
y
x
jk R
R
R. (10.1.8)
C¸c kú väng to¸n häc ë vÕ ph¶i c«ng thøc (10.1.4) thùc chÊt lμ nh÷ng m«men gèc
bËc bèn cña hÖ c¸c ®¹i l−îng ngÉu nhiªn ®ang xÐt. Nh÷ng m«men nμy cã thÓ t×m ®−îc
b»ng c¸ch lÊy vi ph©n hμm ®Æc tr−ng cña hÖ
==τ+ ][)]()([ 2
2
2
1
22 UUMtUtUM xx =
==== 0
2
2
2
1
4321
4
44321
),,,(1
uuuu
uu
uuuuE
i
∂∂
∂
+++++= 122111
2
222
2
11211
2
12 42 RmmRmRmRRR
4222422
2
2
1422 xxxxx mRmmRmm +τ+σ+σ+τ=+ )()( (10.1.9)
Sau khi tÝnh b»ng c¸ch t−¬ng tù nh÷ng gi¸ trÞ cßn l¹i cña c¸c kú väng to¸n häc vμ
thÕ chóng vμo c«ng thøc (10.1.4), ta ®−îc
)].()([)]()([)( τ+τ+τ+τ=τ yyxxyxz RmRmRRR 2222 42 (10.1.10)
§Ó x¸c ®Þnh hμm t−¬ng quan cña hμm ngÉu nhiªn )(tU , khi biÕt hμm t−¬ng quan
cña b×nh ph−¬ng cña nã )(tZ , cÇn cã quy luËt ph©n bè cña )(tU t¹i tõng gi¸ trÞ
t
.
Nh− ®· biÕt (xem môc 1.11) luËt ph©n bè cña modul cña vect¬ hai chiÒu
22
yx UUU += , mμ c¸c thμnh phÇn cña nã lμ nh÷ng ®¹i l−îng ngÉu nhiªn ®éc lËp, ph©n bè
chuÈn, cã cïng ph−¬ng sai 2
σ nh−ng kh¸c kú väng to¸n häc yxx mMmUM == ][,][ y
U , sÏ lμ
hμm Releich tæng qu¸t
201
<
>
σσ
=σ
+
−
.
,
)(
0 khi 0
0 khi
2
0
2
2
2
22
u
u
mu
Ie
u
uf
mu
(10.1.11)
Trong c«ng thøc nμy 22
yx mmm += lμ gi¸ trÞ trung b×nh cña modul vect¬
−
σ2
0
mu
IU; hμm Bessel bËc kh«ng. Khi 1>>
σ
m cã thÓ thay hμm Bessel b»ng biÓu thøc
tiÖm cËn cña nã
....
8
1
1
2
e
)(I0
+
ω
+
πω
≈ω
ω
(10.1.12)
Khi ®ã cã thÓ viÕt
++
π
σ
σ
=σ
−
σ
+
−
...)(
8
1
1
2
22
22
2
2um
e
um
e
u
uf
ummu
. (10.1.13)
Giíi h¹n ë hai sè h¹ng cña chuçi, ta nhËn ®−îc
m
u
um
euf
mu
8
1
2
12
2
(
2
2
σ
+
σπ
≈σ
−
−)
)( . (10.1.14)
Tõ c«ng thøc nμy thÊy r»ng khi 1>>
σ
m víi ®é chÝnh x¸c ®Õn nh©n tö
σ
+m
u
um8
1
2
hμm R¬le tæng qu¸t cã thÓ thay b»ng luËt ph©n bè chuÈn
0ue
2
1
)u(f 2
2
2
)mu
>
σπ
=σ
−
−
khi
(
(10.1.15)
Hμm Releich tæng qu¸t (10.1.11) cã tÝnh bÊt ®èi xøng thÓ hiÖn râ víi nh÷ng trÞ sè
nhá cña σ
m, khi t¨ng σ
m tÝnh bÊt ®èi xøng gi¶m. Khi 2=
σ
m hÖ sè bÊt ®èi xøng b»ng 0,24,
khi 3=
σ
m hÖ sè bÊt ®èi xøng chØ b»ng 0,07.
§Ó n©ng ®é chÝnh x¸c ta sÏ xÊp xØ hμm R¬le tæng qu¸t (10.1.11) b»ng luËt ph©n bè
chuÈn kh«ng ph¶i theo c«ng thøc (10.1.15), mμ d−íi d¹ng
0 khi
2
12
2
2
(
>
σ′
π
=σ′
′
−
−ueuf
mu )
)( (10.1.16)
sau khi chÊp nhËn nh÷ng gi¸ trÞ t−¬ng øng cña kú väng to¸n häc vμ ph−¬ng sai ph©n bè
(10.1.11) lμm kú väng to¸n häc m′ vμ ph−¬ng sai 2
σ′ cña nã.
Nh− ®· biÕt (xem môc 1.11) ®èi víi ph©n bè (10.1.11) kú väng to¸n häc vμ ph−¬ng
sai cã d¹ng
4
2
2
1
2
2
2
2
0
2
22
2
4 2 4 2
1
2
σ
−
σσ
+
σ
σ
+
π
σ=
′
=
m
e
m
I
mm
I
m
muM ][ , (10.1.17)
.][ 2222 2mmuD ′
−+σ=σ′
= (10.1.18)
Trªn h×nh 10.1 dÉn ra c¸c ®−êng cong ph©n bè tÝnh theo c¸c c«ng thøc (10.1.11)
(®−êng cong 1), (10.1.15) (®−êng cong 2) vμ (10.1.16) (®−êng cong 3) víi nh÷ng gi¸ trÞ
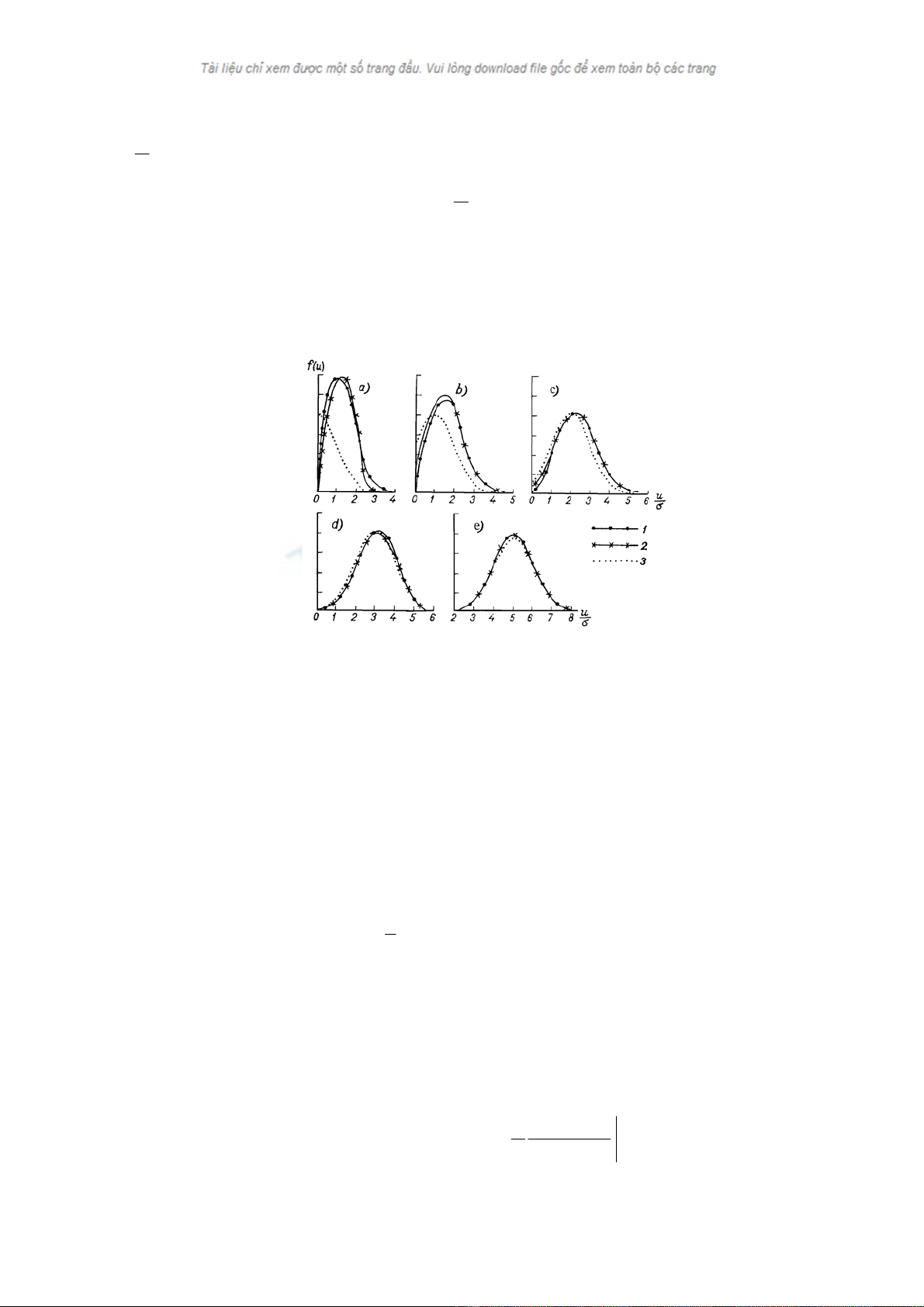
202
5 3, 2 1 0 ,,,=
σ
m. Trªn trôc hoμnh ®Æt c¸c gi¸ trÞ u ®¬n vÞ b»ng σ, trªn trôc tung ®Æt )(uf .
Ph©n tÝch h×nh vÏ thÊy r»ng khi 2≥
σ
m sai sè cña phÐp xÊp xØ ph©n bè (10.1.11)
b»ng ph©n bè chuÈn (10.1.16) lμ rÊt nhá. PhÐp xÊp xØ b»ng ph©n bè (10.1.15) cho kÕt qu¶
kÐm h¬n.
B©y giê ta sÏ coi hμm ngÉu nhiªn )(tU t¹i mçi gi¸ trÞ t tu©n theo qui luËt ph©n bè
chuÈn (10.1.16) víi kú väng to¸n häc m′ vμ ®é lÖch b×nh ph−¬ng trung b×nh σ′ x¸c ®Þnh
theo c¸c c«ng thøc (10.1.17), (10.1.18).
H×nh 10.1
Tr−íc ®©y chóng ta ®· nhËn ®−îc hμm t−¬ng quan cho hμm ngÉu nhiªn )()( tUtZ 2
=.
B©y giê chóng ta thiÕt lËp mèi liªn hÖ gi÷a c¸c hμm t−¬ng quan )(τ
z
R vμ )(τ
u
R.
Hμm t−¬ng quan )(τ
z
R sÏ x¸c ®Þnh theo c«ng thøc
{
−τ+−=τ )([)]]([)([)( tUtUMtUMRz
222
}{
)]()([)]]([ 2222 mtUMtUM ′
+σ′
−=τ+−
}
=
′
+σ′
−τ+× )]()([ 222 mtU
22222 )()]()([ mtUtUM ′
+σ′
−τ+= . (10.1.19)
Ký hiÖu 21 UtUUtU =τ+= )(,)( . V× 1
U vμ 2
U lμ nh÷ng ®¹i l−îng ngÉu nhiªn ph©n bè
chuÈn, nªn hμm ®Æc tr−ng cña hÖ hai ®¹i l−îng ngÉu nhiªn nμy sÏ cã d¹ng
++++−= )()(exp),( 2211
2
2222112
2
11121 2
2
1umumiuRuuRuRuuE , (10.1.20)
trong ®ã
,, 2
221121 σ′
==
′
== RRmmm
)()])([( τ=−−= u
RmUmUMR 221112 . (10.1.21)
)(τ
u
R lμ hμm t−¬ng quan cÇn t×m cña hμm ngÉu nhiªn )(tU .
Ta tÝnh ®¹i l−îng )]()([ τ+tUtUM 22 trong c«ng thøc (10.1.19)
=
∂∂
∂
==τ+ == 0
2
2
2
1
21
4
4
2
2
2
1
22
21
1
uu
uu
uuE
i
UUMtUtUM ),(
][)]()([
)()()( 2222 42 σ′
+
′
−
′
−τ= mtRmR uu . (10.1.22)