189
Ch−¬ng 9: Nh÷ng vÝ dô ngo¹i suy tuyÕn tÝnh tèi −u c¸c qu¸ tr×nh
khÝ t−îng thñy v¨n
9.1. Ngo¹i suy tèi −u dßng ch¶y s«ng theo ph−¬ng ph¸p I. M. Alekhin
I. M. Alekhin ®· øng dông lý thuyÕt ngo¹i suy tuyÕn tÝnh tèi −u c¸c qu¸ tr×nh ngÉu
nhiªn dõng ®Ó dù b¸o dßng ch¶y s«ng ngßi [34]. ¤ng xem ®é lÖch cña dßng ch¶y n¨m so
víi chuÈn nh− mét hμm ngÉu nhiªn dõng cña thêi gian cho t¹i nh÷ng gi¸ trÞ nguyªn cña
®èi sè.
§Ó cã thÓ dù b¸o qu¸ tr×nh ngÉu nhiªn t¹i thêi ®iÓm 0 >+ TTt , theo c¸c sè liÖu
quan tr¾c trªn kho¶ng ®o cña ®èi sè tr−íc thêi ®iÓm t, th× sù tån t¹i mèi phô thuéc t−¬ng
quan ®¸ng kÓ gi÷a c¸c l¸t c¾t cña qu¸ tr×nh ngÉu nhiªn lμ cÇn thiÕt. Cã thÓ nhËn ®Þnh vÒ
sù tån t¹i mèi phô thuéc nμy, ch¼ng h¹n, b»ng ®å thÞ hμm t−¬ng quan. Trong [34] ®·
tÝnh c¸c hμm t−¬ng quan chuÈn ho¸ )(τr cña ®é lÖch dßng ch¶y n¨m so víi chuÈn cho s¸u
con s«ng ph©n bè trªn l·nh thæ ch©u ¢u cña Liªn X«. Sè liÖu ban ®Çu ®Ó tÝnh lμ sè liÖu
l−u l−îng n−íc trung b×nh n¨m trong 50−70 n¨m lÊy tõ "Tμi liÖu chÕ ®é s«ng ngßi Liªn
X«" vμ c¸c niªn lÞch thñy v¨n. Nh÷ng vÝ dô vÒ c¸c hμm t−¬ng quan ®· tÝnh ®−îc dÉn trªn
h×nh 9.1. (Nh÷ng ®−êng liÒn nÐt nhËn ®−îc b»ng c¸ch lμm tr¬n theo ph−¬ng ph¸p b×nh
ph−¬ng tèi thiÓu). Tõ h×nh 9.1, rót ra kÕt luËn vÒ nguyªn t¾c cã thÓ dù b¸o dßng ch¶y
s«ng, v× t−¬ng quan l−u l−îng trung b×nh n¨m trong s¸u tr−êng hîp xem xÐt tá ra kh¸
cao trong mét d¶i réng cña kho¶ng τ. §iÒu nμy, theo Iu. M. Alokhin, ®−îc quyÕt ®Þnh bëi
hai nguyªn nh©n: sù ®iÒu chØnh dßng ch¶y n¨m t¹o nªn mèi liªn hÖ t−¬ng quan víi
nh÷ng τ kh«ng lín (kh«ng lín h¬n 2−3 n¨m), vμ tÝnh chu kú cña dßng ch¶y t¹o nªn sù
t−¬ng quan biÕn thiªn cã tÝnh tuÇn hoμn vμ lμm cho t−¬ng quan t¾t dÇn chËm trong d¶i τ
réng. Trong c«ng tr×nh [34] ®· kh¶o s¸t ngo¹i suy "thuÇn tuý" (kh«ng lμm tr¬n) dßng
ch¶y n¨m cña c¸c con s«ng víi thêi h¹n dù b¸o 3 2 1 ,,=T vμ 5 n¨m. Trong ®ã c¸c tÝnh
to¸n ®−îc thùc hiÖn b»ng hai ph−¬ng ph¸p: gi¶i trùc tiÕp hÖ ph−¬ng tr×nh ®¹i sè (5.2.11)
(xem môc 5.2) vμ sö dông lý thuyÕt Kolmogorov−Winer (xem môc 5.3 vμ 5.5).
190
H×nh 9.1
1. Dù b¸o dßng ch¶y s«ng b»ng c¸ch gi¶i trùc tiÕp hÖ ph−¬ng tr×nh ®¹i sè
Bμi to¸n dù b¸o dßng ch¶y s«ng ®−îc ®Æt ra nh− sau. Cã sè liÖu ®é lÖch dßng ch¶y
n¨m so víi chuÈn )(),(),( ntqtqtq −− ..., 1 ghi ®−îc trong n n¨m mμ n¨m cuèi cïng ®−îc ký
hiÖu lμ t. Gi¸ trÞ dù b¸o )( Ttq +, víi −
T
thêi h¹n dù b¸o, sÏ ®−îc t×m d−íi d¹ng tæ hîp
tuyÕn tÝnh cña m sè trong sè c¸c sè liÖu nμy
=
−α=+
m
k
kktqTtq
0
)()( . (9.1.1)
C¸c hÖ sè
k
α®èi víi tõng gi¸ trÞ
T
®· cho, ®−îc x¸c ®Þnh tõ ®iÒu kiÖn cùc tiÓu
ph−¬ng sai sai sè ngo¹i suy nh− ®· tr×nh bμy trong môc 5.2, lμ nghiÖm cña hÖ ph−¬ng
tr×nh
=
=−α=+
m
k
qkq mjjkRjTR
1
..., 2 1 ,,),()( , (9.1.2)
trong ®ã )(τ
q
R lμ hμm t−¬ng quan cña ®é lÖch dßng ch¶y n¨m. Sè h¹ng tö m trong tæng
(9.1.1) cÇn ®−îc chän sao cho c¸c m«men t−¬ng quan )( jkRq− x¸c ®Þnh theo sè liÖu quan
tr¾c t¹i n ®iÓm ph¶i ®ñ tin cËy. Trong [34], hÖ ph−¬ng tr×nh (9.1.2) ®−îc gi¶i b»ng
ph−¬ng ph¸p Gauss [77].
Chóng ta sÏ xem xÐt kÕt qu¶ tÝnh cho s«ng Volga t¹i Kub−shev. Chuçi ban ®Çu cña l−u
l−îng trung b×nh n¨m lÊy b»ng c¸c ®é lÖch so víi chuÈn trong thêi kú 1882−1935. Sè h¹ng tö
trong tæng (9.1.1) b»ng 21.
Trong b¶ng 9.1 dÉn ra gi¸ trÞ cña c¸c hÖ sè ngo¹i suy tèi −u
k
αøng víi thêi h¹n dù
b¸o 3 2 1 ,,=T vμ 5 n¨m.
§Ó ®¸nh gi¸ chÊt l−îng dù b¸o tèi −u, trªn h×nh 9.2 dÉn ra nh÷ng gi¸ trÞ thùc cña
dßng ch¶y n¨m (®−êng liÒn nÐt) vμ nh÷ng gi¸ trÞ dù b¸o theo c«ng thøc (9.1.1) víi c¸c hÖ
sè ë b¶ng 9.1.
Tõ h×nh 9.2 thÊy r»ng, sè liÖu dù b¸o nhËn ®−îc theo ph−¬ng ph¸p ngo¹i suy tèi −u
kh¸ phï hîp víi nh÷ng gi¸ trÞ thùc cña dßng ch¶y n¨m.
B¶ng 9.1
k
T
0 1 2 3 4 5 6 7 8 9 10
1 0,56
−0,53 0,42 −0,22 0,03 0,08 −0,28 0,03 0,24 0,18 0,00
2 −0,22 0,19 −0,07 −0,28 −0,05 −0,17 0,02 0,25 0,19 0,13 0,19
3 −0,19 0,11 −0,55 0,16 −0,38 0,08 0,20 0,23 0,00 0,14 0,13
5 −0,85 −0,06 −0,52 0,53 −0,01 0,28 −0,18 0,25 −0,02 0,34 0,58
k
T
11 12 13 14 15 16 17 18 19 20
1 0,22 0,03 0,35 −0,17 −0,29 0,22 −0,48 0,08 −0,21 0,00
2 0,08 0,34 0,14 −0,17 0,08 −0,36 −0,07 −0,15 −0,16 −0,33
3 0,35 0,20
−0,23 0,31 −0,26 −0,17 0,00 −0,28 −0,15 −0,30
5 0,01 0,28
−0,44 0,07 0,00 −0,49 −0,42 −0,52 0,32 −0,04
191
C¸c hÖ sè t−¬ng quan gi÷a gi¸ trÞ thùc vμ dù b¸o b»ng:
030840 ,, ± víi 1=
T
n¨m,
030840 ,, ± víi 2=
T
n¨m,
030840 ,, ± víi 3=
T
n¨m,
030800 ,, ± víi 5=
T
n¨m.
Thμnh c«ng cña viÖc ®−a sè liÖu nhiÒu n¨m vμo dù b¸o cμng thÓ hiÖn râ nÕu chóng ta
nhí l¹i r»ng c¸c hÖ sè t−¬ng quan gi÷a l−u l−îng trung b×nh n¨m cña s«ng Volga (t¹i
Kub−shev) víi 3 2,=τ vμ 5 n¨m b»ng 0602 ,)( =r,0503 ,)( −=r, 2305 .)( −=r (xem h×nh 9.1).
KÕt qu¶ dù b¸o cho n¨m con s«ng kh¸c còng rÊt kh¶ quan.
H×nh 9.2
2. Dù b¸o dßng ch¶y s«ng khi sö dông lý thuyÕt Kolmogorov− Winer
Gi¶ thiÕt r»ng ®é lÖch dßng ch¶y n¨m so víi chuÈn lμ qu¸ tr×nh ngÉu nhiªn dõng vμ
kho¶ng thêi gian cho qu¸ tr×nh nμy kh¸ lín, tøc lμ thÓ hiÖn cña qu¸ tr×nh cã thÓ xem lμ
®−îc cho trªn toμn kho¶ng tr−íc thêi ®iÓm hiÖn t¹i.
Theo lý thuyÕt Kolmogorov−Winer gi¸ trÞ dù b¸o )( Ttq + ®−îc t×m theo c«ng thøc
(9.1.1), trong ®ã c¸c hÖ sè k
α ®−îc x¸c ®Þnh b»ng c¸ch gi¶i ph−¬ng tr×nh Winer−Hopf
theo ph−¬ng ph¸p ®· tr×nh bμy trong môc 5.5.
Ph−¬ng ph¸p tÝnh to¸n nh− sau:
1) t×m hμm t−¬ng quan )(τ
q
R theo chuçi c¸c quan tr¾c )(tq , )( 1−tq ,..., )( ntq −,
2) t×m mËt ®é phæ )(ω
q
S theo hμm t−¬ng quan )(τ
q
R,
3) x¸c ®Þnh hμm truyÒn tèi −u theo c«ng thøc (5.5.19),
4) x¸c ®Þnh c¸c hÖ sè
k
α nh− lμ gi¸ trÞ cña hμm träng l−îng tèi −u (5.4.11) khi
thay thÕ t bëi kt − trong c«ng thøc nμy,
5) x¸c ®Þnh gi¸ trÞ cÇn t×m )( Ttq + theo c«ng thøc (9.1.1).
Trong ch−¬ng 5 chóng ta ®· xÐt ph−¬ng ph¸p x¸c ®Þnh hμm träng l−îng tèi −u khi
cho hμm t−¬ng quan cña qu¸ tr×nh ngÉu nhiªn d−íi d¹ng gi¶i tÝch. Khi ®ã gi¶ thiÕt r»ng
nh÷ng gi¸ trÞ thèng kª cña hμm t−¬ng quan tÝnh theo sè liÖu thùc nghiÖm ®−îc xÊp xØ
b»ng biÓu thøc gi¶i tÝch.
192
Trong [34] nh÷ng gi¸ trÞ thèng kª cña hμm t−¬ng quan ®−îc xÊp xØ b»ng ®−êng gÊp
khóc, ë ®ã tÝch ph©n trong c¸c c«ng thøc x¸c ®Þnh mËt ®é phæ, hμm truyÒn vμ hμm träng
l−îng ®−îc thay thÕ gÇn ®óng b»ng tæng tÝch ph©n t−¬ng øng khi tÝnh to¸n.
B¶ng 9.2
k 0 1 2 3 4 5 6 7 8 9 10
k
α 0,40 0,00 0,00 −0,30 0,53 0,25 0,21 0,10 0,21 −0,14 −0,11
k 11 12 13 14 15 16 17 18 19 20
k
α0,14 −0,05 0,47 −0,06 −0,30 0,10 −0,06 −0,10 0,14 −0,11
Trong b¶ng 9.2 dÉn ra nh÷ng gi¸ trÞ nhËn ®−îc cña c¸c hÖ sè k
α ®èi víi s«ng Volga
víi thêi gian b¸o tr−íc b»ng mét n¨m.
Sö dông c¸c hÖ sè k
α trong b¶ng 9.2, theo c«ng thøc (9.1.1) ®· lμm dù b¸o dßng
ch¶y s«ng Volga t¹i Kub−shev víi thêi h¹n dù b¸o 1 n¨m cho thêi kú 1902−1935. Trªn
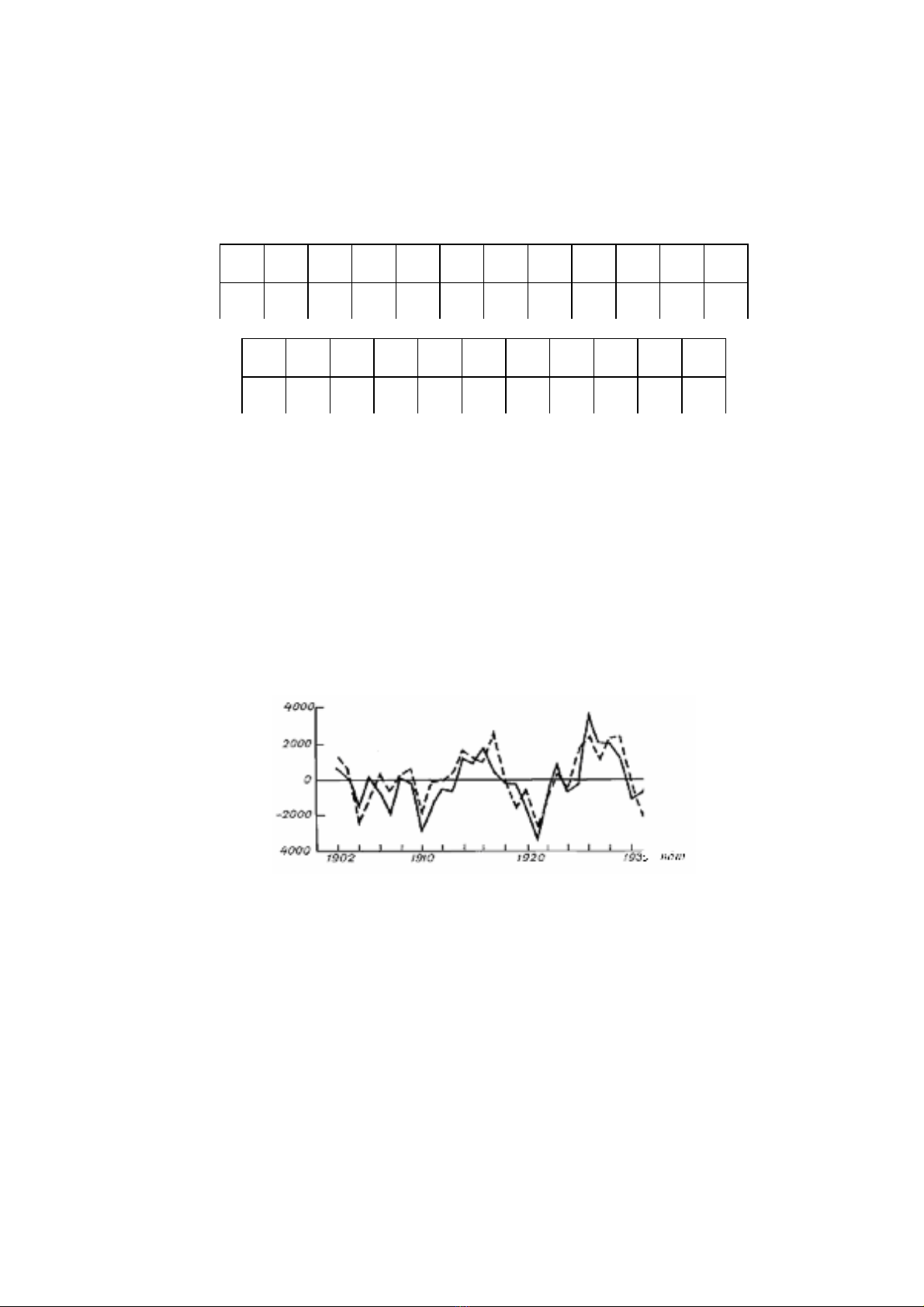
h×nh 9.3 dÉn ra nh÷ng sè liÖu tÝnh to¸n dù b¸o (®−êng g¹ch nèi) vμ gi¸ trÞ quan tr¾c
thùc cña ®é lÖch dßng ch¶y so víi chuÈn trong nh÷ng n¨m ®ã (®−êng liÒn nÐt). Tõ h×nh vÏ
thÊy r»ng, sè liÖu tÝnh ph¶n ¸nh ®óng biÕn tr×nh cña gi¸ trÞ thùc vμ kh¸ phï hîp víi
chóng. HÖ sè t−¬ng quan cña dßng ch¶y thùc vμ dù b¸o b»ng 030860 ,, ±. So s¸nh c¸c kÕt
qu¶ nμy víi nh÷ng ®¸nh gi¸ dù b¸o nhËn ®−îc b»ng con ®−êng gi¶i trùc tiÕp hÖ ph−¬ng
tr×nh (9.1.2) (xem môc 1) thÊy r»ng ®é chÝnh x¸c cña chóng xÊp xØ nh− nhau.
H×nh 9.3
9.2. Ph©n tÝch phæ vμ ngo¹i suy chØ sè hoμn l−u vÜ h−íng
Khi nghiªn cøu c¸c qu¸ tr×nh khÝ quyÓn quy m« lín cÇn biÕt quy luËt cña m¾t xÝch chñ
yÕu trong hoμn l−u chung cña khÝ quyÓn, ®ã lμ hoμn l−u vÜ h−íng, tøc sù vËn chuyÓn kh«ng
khÝ tõ phÝa t©y sang phÝa ®«ng g©y nªn bëi dßng nhiÖt tíi tõ mÆt trêi vμ sù quay cña tr¸i ®Êt
quanh trôc.
Khi t×m hiÓu c¸c quy luËt hoμn l−u th−êng ng−êi ta sö dông mét sè ®Æc tr−ng tÝch ph©n
cña c¸c qu¸ tr×nh vÜ m«. Phæ biÕn nhÊt trong c¸c ®Æc tr−ng ®ã lμ chØ sè hoμn l−u vÜ h−íng.
ChØ sè hoμn l−u vÜ h−íng J ®−îc ®Þnh nghÜa nh− lμ mét ®¹i l−îng kh«ng thø nguyªn,
b»ng tû sè tèc ®é gãc quay cña khÝ quyÓn α vμ tèc ®é gãc quay cña tr¸i ®Êt
ω
193
ω
α
=J. (9.2.1)
§¹i l−îng α liªn hÖ víi tèc ®é dμi cña chuyÓn ®éng khÝ quyÓn bëi hÖ thøc
ϕα=
λcos)( 0
rzv , (9.2.2)
trong ®ã λ
v lμ tèc ®é cña dßng vÜ h−íng, −
0
r b¸n kÝnh trung b×nh tr¸i ®Êt,
ϕ
lμ vÜ ®é ®Þa lý,
−
z
®é cao trªn mùc n−íc biÓn.
Do tÇm quan träng cña sù hiÓu biÕt vÒ nh÷ng quy luËt biÕn ®æi theo thêi gian cña chØ sè
hoμn l−u vÜ h−íng, ®Æc biÖt cho môc ®Ých hoμn thiÖn ph−¬ng ph¸p dù b¸o thêi tiÕt h¹n dμi,
trong nhiÒu c«ng tr×nh ®· nghiªn cøu cÊu tróc thèng kª cña chØ sè hoμn l−u vÜ h−íng vμ thö
nghiÖm dù b¸o nã b»ng ph−¬ng ph¸p thèng kª.
H×nh 9.4
Trong c¸c c«ng tr×nh [49, 53, 54, 61, 82] ®· tiÕn hμnh xö lý thèng kª mét sè l−îng kh¸
lín tμi liÖu thùc nghiÖm vμ tÝnh c¸c hμm t−¬ng quan, mËt ®é phæ cña chØ sè hoμn l−u vÜ
h−íng.
Trªn h×nh 9.4 dÉn ra c¸c hμm t−¬ng quan thêi gian cña chØ sè hoμn l−u vÜ h−íng theo
[49] ®èi víi c¸c ®é cao cña c¸c mÆt ®¼ng ¸p 1000, 700, 500, 300, 200 vμ 100mb.
C¸c hμm t−¬ng quan ®−îc tÝnh theo gi¸ trÞ ngμy cña ®¹i l−îng chØ sè hoμn l−u vÜ h−íng
trong nh÷ng n¨m quan tr¾c sau ®©y:
Mùc,
mb
N¨m
1000
700,
500
300,
200
100
1955−1
960
1949−1
960
1954−1
956
1958−1
960
1958−1
960