Baøi giaûng Kyõ Thuaät Ñieän Ñaïi Cöông ©TCBinh
Chöông 1: Maïch töø trong thieát bò kyõ thuaät ñieän 1
Chöa caäp nhaät
Chöông 1: MAÏCH TÖØ
I.1. Khaùi nieäm chung
I.1.1. Caùc coâng thöùc cô baûn
Ñònh luaät doøng ñieän toaøn phaàn (hay ñònh luaät löu soá Ampeøre - Maxwell)
∫∫ =
Al
AdJld.H
r
r
r
r (1.1)
H: cöôøng ñoä töø tröôøng (A voøng /m)
J: maät ñoä doøng ñieän (A/m2)
(Tích phaân ñöôøng cong cuûa cöôøng ñoä töø tröôøng H
r
doïc theo moät maïch voøng kheùp
kín l baèng toång ñaïi soá cöôøng ñoä caùc doøng ñieän ñi xuyeân qua beà maët A baát kyø ñöôïc
bao bôûi voøng kín l.)
Ñònh luaät Gauss ñoái vôùi töø tröôøng:
∫=
S
0Sd.B
r
r (1.2)
B: Caûm öùng töø (T -Tesla)
(Thoâng löôïng cuûa vector caûm öùng töø B
r
(hay töø thoâng) qua maët kín S tuøy yù luoân
baèng khoâng.)
Ñònh luaät Kirchhoff 1 ñoái vôùi maïch ñieän: 0I
n
1k
k=
∑
=
Ñònh luaät Kirchhoff 2 ñoái vôùi maïch ñieän: 0RIU
p
1k
kk
n
1i
i=+ ∑∑ ==
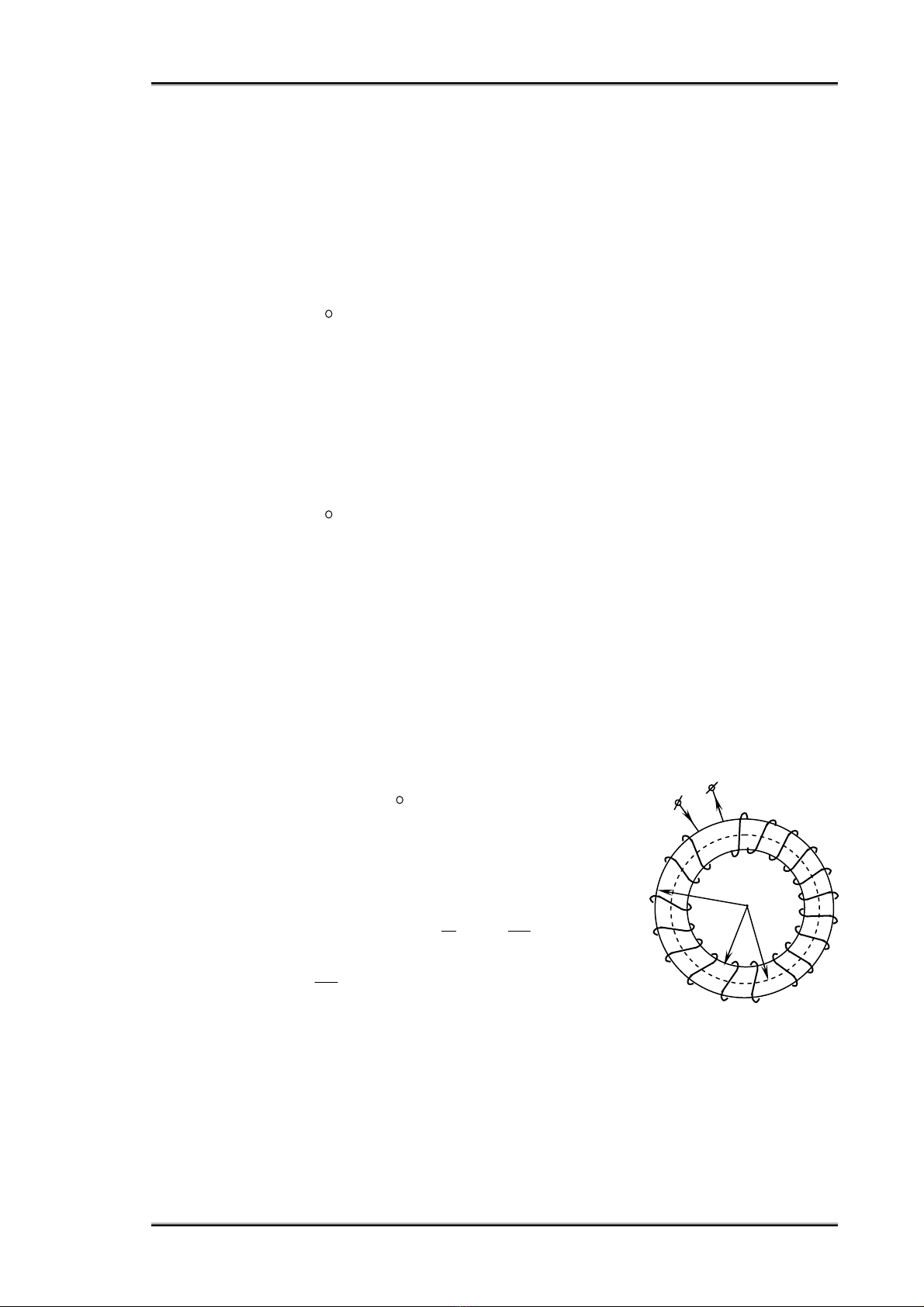
Ñoái vôùi maïch töø kín chieàu daøi l coù N doøng ñieän I chaïy qua sinh ra
cöôøng ñoä töø tröôøng ñeàu H (hình 1.1):
Khi ñoù, phöông trình ∫∫ =
Al
AdJld.H
r
r
r
r
coù theå vieát
thaønh: N.I = H.l
Goïi F = N.I söùc töø ñoäng
Φ = B.S töø thoâng qua tieát dieän S
Coù: F = NI = Hl = m
R
S
l
BSl
BΦ=
μ
=
μ
Vôùi S
l
Rm
μ
= [1/H] töø trôû cuûa maïch töø.
μ [H/m] ñoä töø thaåm
mm RU Φ= [A.vòng] ñöôïc goïi laø töø aùp.
Ñònh luaät Kirchhoff 2 ñoái vôùi maïch töø:
0RF
p
1k
mkk
n
1i
i=Φ+ ∑∑ ==
()
Ñoái vôùi moät maïch voøng kheùp kín trong maïch töø, toång caùc töø aùp rôi treân maïch
voøng ñoù vaø caùc söùc töø ñoäng laø baèng khoâng.
I
R
R
1
R
2
Hình 1.1
Baøi giaûng Kyõ Thuaät Ñieän Ñaïi Cöông ©TCBinh
Chöông 1: Maïch töø trong thieát bò kyõ thuaät ñieän 2
Ñònh luaät Kirchhoff 1 ñoái vôùi maïch töø:
0
n
1i
i=Φ
∑
=
(hình 1.2)
Ñoái vôùi moät nuùt baát kyø trong maïch töø, toång caùc töø thoâng ñi vaøo vaø ñi ra khoûi nuùt
baèng khoâng.
I.1.2. Sô ñoà thay theá cuûa maïch töø
S
R
o
μ
δ
=
δ laø töø trôû khe hôû khoâng khí (boû qua töø taûn)
R
σ laø töø trôû roø töø loõi naøy sang loõi kia
μo = 4π.10-7 (H/m) haèng soá töø hay ñoä töø thaåm chaân khoâng
δ
δ=R
1
G laø töø daãn khe hôû khoâng khí
δ
μ
δ
δ
S
R
1
Go
== laø töø daãn khe hôû khoâng khí (boû qua töø taûn)
Neáu khoâng boû qua töø taûn:
δ
μ
σ
δ
S
Go
t
=
vôùi heä soá taûn: 1
t≥
σ
vaø heä soá roø:
lvlv
lv
lv
o
r1Φ
Φ
+=
Φ
Φ
+
Φ
=
Φ
Φ
=σ σσ (1.7, 1.9)
vì
(
)
Σ
+
Φ
=Φ
δσσ
RRR nlv
⇒ø
Σδ
σ
σ
Σδ
σ
Σδσ =≈
+
=
Φ
Φ
G
G
R
R
R
RR n
lv
(
Σδ
<RR n)
⇒
Σδ
σ
+=σ G
G
1
r (1.13)
Baûng 1.1: Töông töï giöõa maïch ñieän vaø maïch töø
(xem saùch)
Rδ = 2Rδ
Φl
v
N
Φ0
g
oân
g
loõi
naé
p
I
IN
Φ0
Rn
R
δ
Φlv
RδR
σ
Φ
RlRl
Rg
Φ0
IN
Rn
Φlv
Rσ
Φ
Rl 2Rl
Rg
δ
Φ0
Φ
σ
Baøi giaûng Kyõ Thuaät Ñieän Ñaïi Cöông ©TCBinh
Chöông 1: Maïch töø trong thieát bò kyõ thuaät ñieän 3
I.1.3. Ñaëc tính cuûa vaät lieäu saéc töø
Ñöôøng cong B(H) cuûa vaät lieäu saéc töø khi töø tröôøng ngoaøi taùc ñoäng laø töø
tröôøng moät chieàu (hình 1.7):
HHB ro
r
r
r
μμ=μ=
vôùi μo = 4π.10-7 (H/m)
Vaät lieäu saéc töø: )H(
rr
μ
=μ (phi tuyeán vaø coù giaù trò töø vaøi chuïc ñeán vaøi
chuïc ngaøn).
Vaät lieäu phi töø tính: 1
r
≈
μ
Ñöôøng cong B(H) cuûa vaät lieäu saéc töø khi töø tröôøng ngoaøi taùc ñoäng laø töø
tröôøng xoay chieàu (hình 1.8):
Vaät lieäu saéc töø chia laøm nhieàu vuøng con (10-2 ÷ 10-6 cm3) ñöôïc töø hoùa coù
caùc momen cuûa caùc nguyeân töû ñöôïc ñònh höôùng song song nhau.
Traïng thaùi baûo hoøa: caùc momen töø cuûa caùc vuøng con ñeàu höôùng theo chieàu
taùc ñoäng cuûa töø tröôøng ngoaøi (traïng thaùi töø hoùa giôùi haïn).
Hieän töôïng töø treã: laø hieän töông khi giaûm cöôøng ñoä töø tröôøng ngoaøi, B
giaûm chaäm hôn khi taêng. Khi cöôøng ñoä töø tröôøng ngoaøi baèng 0 thì
0BB r≠= goïi laø töø dö.
Hc laø löïc khaùng töø: cöôøng ñoä töø tröôøng ngöôïc ñeå B=0.
Hình 1.8 veõ chu trình töø treã.
Khi töø tröôøng ngoaøi xoay chieàu taùc
ñoäng, vaät lieäu saéc töø bò töø hoùa tuaàn hoaøn
theo voøng töø treã, gaây neân söï phaùt noùng
do ma saùt noäi boä khi caùc momen töø ñoåi
chieàu.
Dieän tích voøng töø treã caøng lôùn hay taàn
soá cuûa töø tröôøng ngoaøi caøng cao thì toån
hao caøng lôùn.
(Coøn laïi SV töï ñoïc saùch)
I.1.4. Caùc baøi toaùn cuûa maïch töø
Baøi toaùn thuaän
o Cho: Φ hay B, kích thöôùc maïch töø, ñöôøng cong B(H)
o Tính: söùc töø ñoäng F
Baøi toaùn nghòch
o Cho: F
o Tính: caùc giaù trò töø thoâng trong maïch töø
Hình 1.8
H
B
Br
-Hc
1
2
3
4
5
Baøi giaûng Kyõ Thuaät Ñieän Ñaïi Cöông ©TCBinh
Chöông 1: Maïch töø trong thieát bò kyõ thuaät ñieän 4
I.2. Maïch töø moät chieàu
I.2.1. Tính toaùn maïch töø moät chieàu khi boû qua töø trôû cuûa loõi theùp
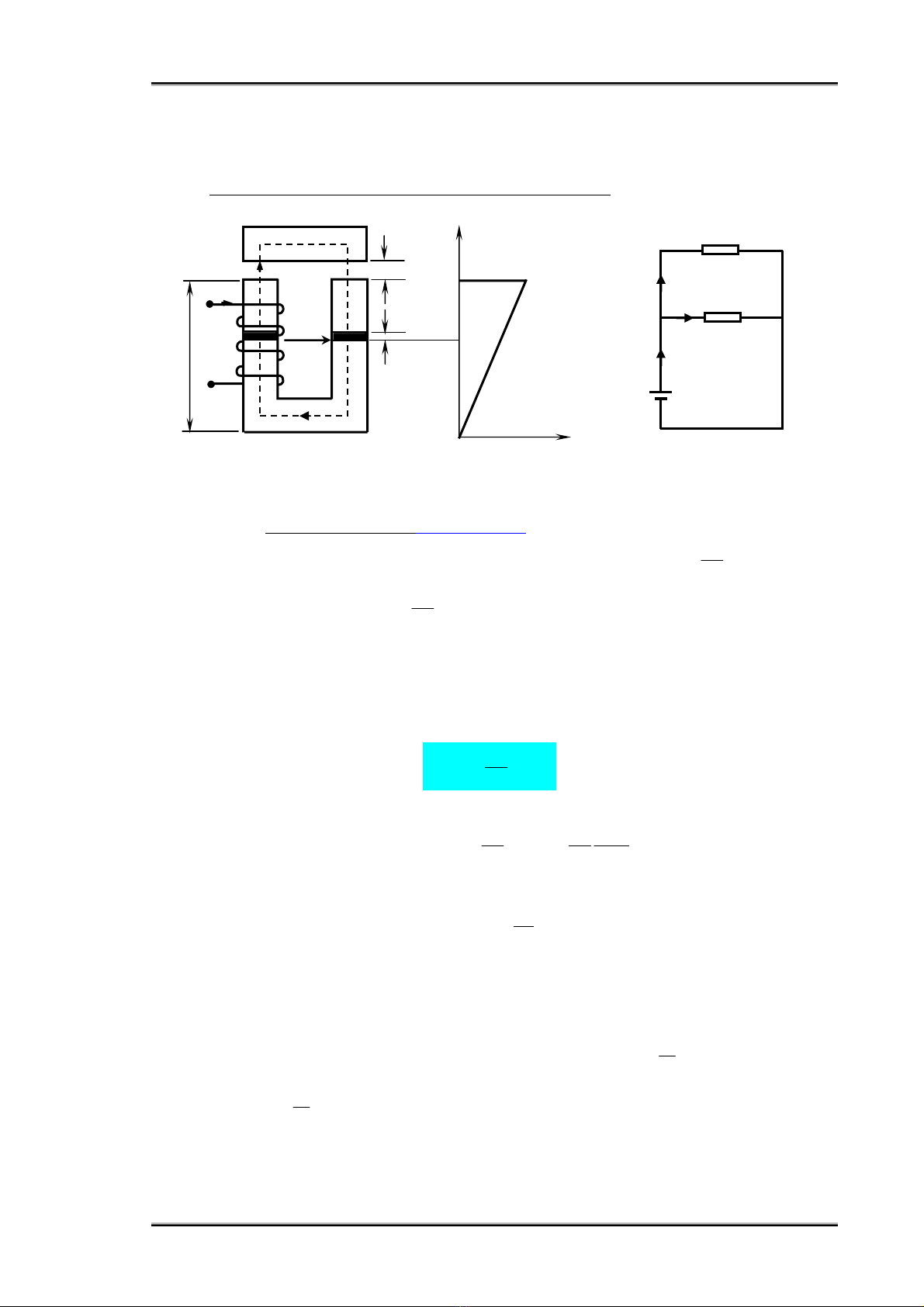
Cuoän daây quaán treân loõi cuûa maïch töø (hình 1.11):
¾ Töø daãn roø qui ñoåi theo töø thoâng
Söùc töø ñoäng treân moät ñôn vò chieàu daøi cuoän daây cuoän daây: l
IN
Töø aùp treân ñieåm x: x
l
IN
Fx=
Töø daãn roø treân moät ñôn vò chieàu daøi loõi: g
Töø daãn roø cuûa ñoaïn maïch dx: dx.gdG x
=
σ
Vi phaân töø thoâng roø cuûa ñoaïn maïch töø dx ôû vò trí x:
xxx dGFd σσ
=
Φ
hay gdx.x
l
IN
dx=Φσ
Töø thoâng roø treân ñoaïn loõi maïch töø (0÷x):
2
x.g
l
IN
gdx.x
l
IN
d
2
x
0
x
0
xx ==Φ=Φ ∫∫ σσ
Töø thoâng roø treân ñoaïn loõi maïch töø (0÷l):
2
l.g
IN
l=Φσ
Töø thoâng laøm vieäc khi boû qua töø trôû loõi theùp:
Σδ
=
Φ
G.IN
lv
Töø thoâng toång qua goâng:
()
⎟
⎠
⎞
⎜
⎝
⎛+=+=Φ+Φ=Φ ΣδσΣδσ 2
gl
GINGGIN
llvo
Vôùi 2
gl
G=
σ laø töø daãn roø qui ñoåi theo töø thoâng
(Thay theá töø thoâng roø phaân boá doïc theo chieàu daøi loõi baèng töø thoâng roø taäp trung
taïi moät ñieåm.)
δ
φ0
dΦσ
N
I
dx
lcd =1
0
l IN
IN
x
Φ0
IN
Gδ
∑
Φlv
Gσ
Φσ
Hình 1.10
Baøi giaûng Kyõ Thuaät Ñieän Ñaïi Cöông ©TCBinh
Chöông 1: Maïch töø trong thieát bò kyõ thuaät ñieän 5
¾ Töø daãn roø qui ñoåi theo töø thoâng moùc voøng
Ñoä töï caûm II
Llv σ
Ψ
+
Ψ
=
Ψ
= (Ψ laø töø thoâng moùc voøng)
Coù: Σδ
=Φ=Ψ IGNN 2
lvlv
Vaø ∫Φ
⎟
⎠
⎞
⎜
⎝
⎛
=Ψ
l
0
x
d
l
x
N
σσ
vôùi gdx.x
l
IN
dx=Φσ vaø
⎟
⎠
⎞
⎜
⎝
⎛
l
x
N: soá voøng daây
neân 3
gl
INdxx
l
gIN
l
0
22
2
2
∫==Ψσ
Vaäy coù: ⎟
⎠
⎞
⎜
⎝
⎛+= Σδ 3
gl
GNL 2
Vôùi 3
gl
G=
σ laø töø daãn roø qui ñoåi theo töø thoâng moùc voøng. Söû duïng cho nam
chaâm ñieän laøm vieäc ôû cheá ñoä quaù ñoä hay nam chaâm ñieän xoay chieàu.
(Thay theá töø thoâng roø moùc voøng phaân boá doïc theo chieàu daøi loõi baèng töø thoâng roø
moùc voøng qua N voøng daây sao cho L cuoän daây khoâng ñoåi)
Boû qua töø thoâng roø thì: Σδ
=GNL 2
Cuoän daây quaán treân goâng cuûa maïch töø:
Tính toaùn töông töï nhö treân, töø daãn roø qui ñoåi theo töø thoâng vaø töø thoâng moùc
voøng baèng nhau: glG =
σ
¾ Töø daãn roø qui ñoåi theo töø thoâng
Töø daãn roø cuûa ñoaïn maïch dx: dx.gdG x
=
σ
Vi phaân töø thoâng roø cuûa ñoaïn maïch töø dx ôû vò trí x: gdx.INFdGd xx ==
Φ
σσ
Töø thoâng roø treân ñoaïn loõi maïch töø (0÷l):
gl.INgdx.INd
l
0
l
0
xl ==Φ=Φ ∫∫ σσ
Vôùi
glG
=
σ laø töø daãn roø qui ñoåi theo töø thoâng khi cuoän daây ñöôïc quaán treân
goâng cuûa maïch töø.
¾ Töø daãn roø qui ñoåi theo töø thoâng moùc voøng
Töø thoâng moùc voøng cuûa töø thoâng roø
∫∫ ==Φ=Ψ σσ
l
0
22
l
0
xglINgdxINNd
Vôùi glG
=
σ laø töø daãn roø qui ñoåi theo töø thoâng moùc voøng khi cuoän daây ñöôïc
quaán treân goâng cuûa maïch töø.
I.2.2. Tính toaùn maïch töø moät chieàu khi khoâng boû qua töø trôû loõi theùp
Giaûi baøi toaùn baèng phöông phaùp laëp:
(SV töï ñoïc saùch)