C7. Moâ Taû Toaùn Hoïc Heä Thoáng ÑK Rôøi Raïc 1
Chöông 7
MOÂ TAÛ TOAÙN HOÏC
HEÄ THOÁNG ÑIEÀU KHIEÅN RÔØI RAÏC
C7. Moâ Taû Toaùn Hoïc Heä Thoáng ÑK Rôøi Raïc 2
7.1 Heä Thoáng Ñieàu Khieån Rôøi Raïc
7.1.1 Khaùi nieäm
• Heä thoáng rôøi raïc : Tín hieäu ñöôïc löôïng töû hoùa theo thôøi gian coøn bieân ñoä
thì lieân tuïc.
• Heä thoáng soá : Tín hieäu ñöôïc löôïng töû hoùa theo thôøi gian vaø bieân ñoä cuõng
ñöôïc löôïng töû hoùa.
• Coù thôøi gian treã do laáy maãu → vieäc oån ñònh cuûa heä thoáng trôû neân phöùc taïp
→ caàn coù nhöõng kyõ thuaät ñaëc bieät.
• Phoå bieán trong caùc heä thoáng ÑK hieän ñaïi
(), ()
R
utct
: tín hieäu lieân tuïc
(),(),()
ht
rkT ukT c kT , : tín hieäu soá
• Hieän chöa coù pp moâ taû chính xaùc sai soá löôïng töû bieân ñoä caùc boä A/D, D/A
→ khaûo saùt heä thoáng rôøi raïc (boû qua sai soá löôïng töû bieân ñoä öùng vôùi ñoä
phaân giaûi nhoû.
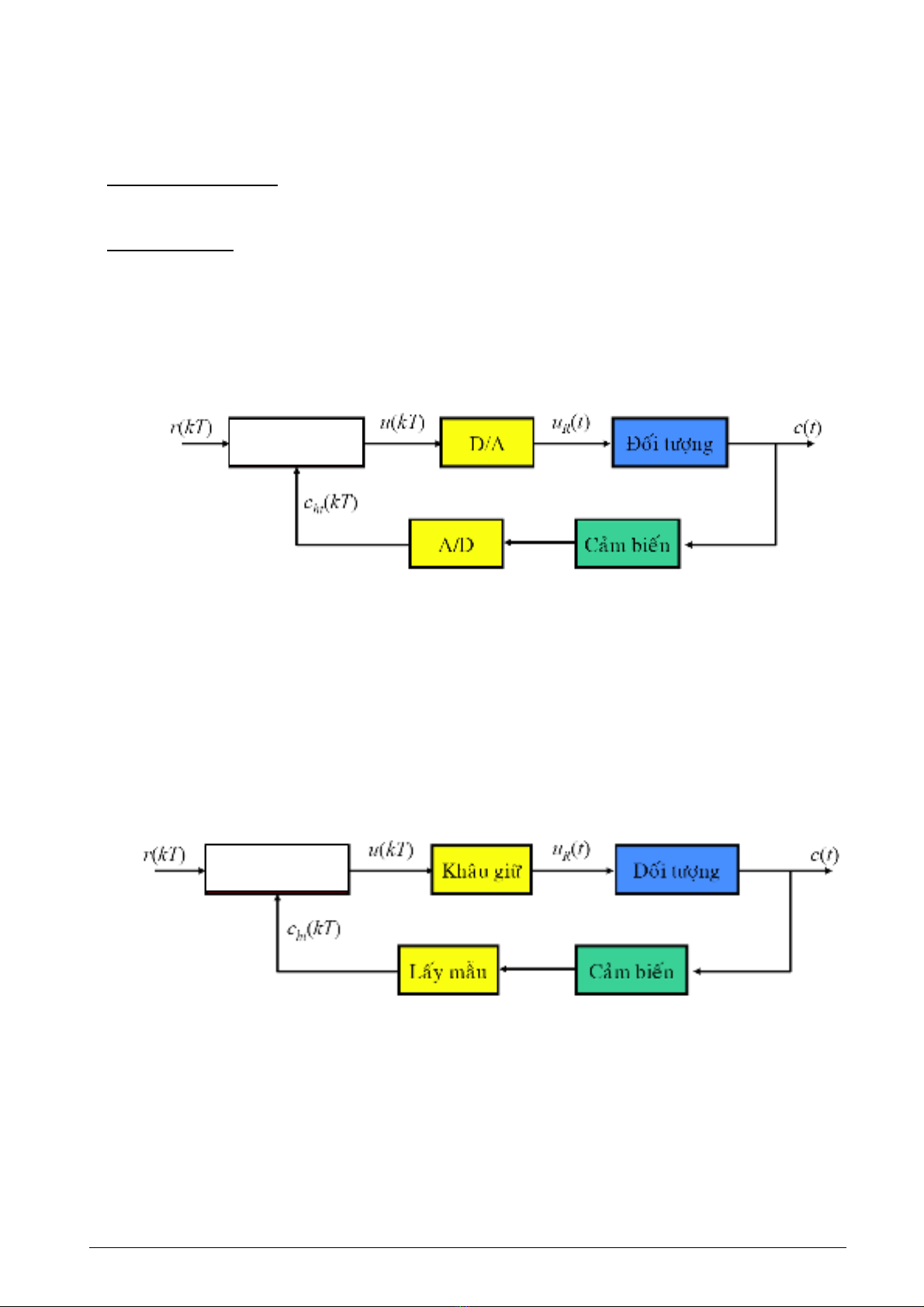
Sô ñoà khoái heä thoáng ñieàu khieån soá
Sô ñoà khoái heä thoáng ñieàu khieån rôøi raïc
Maùy tính soá
Xöû lyù rôøi raïc
C7. Moâ Taû Toaùn Hoïc Heä Thoáng ÑK Rôøi Raïc 3
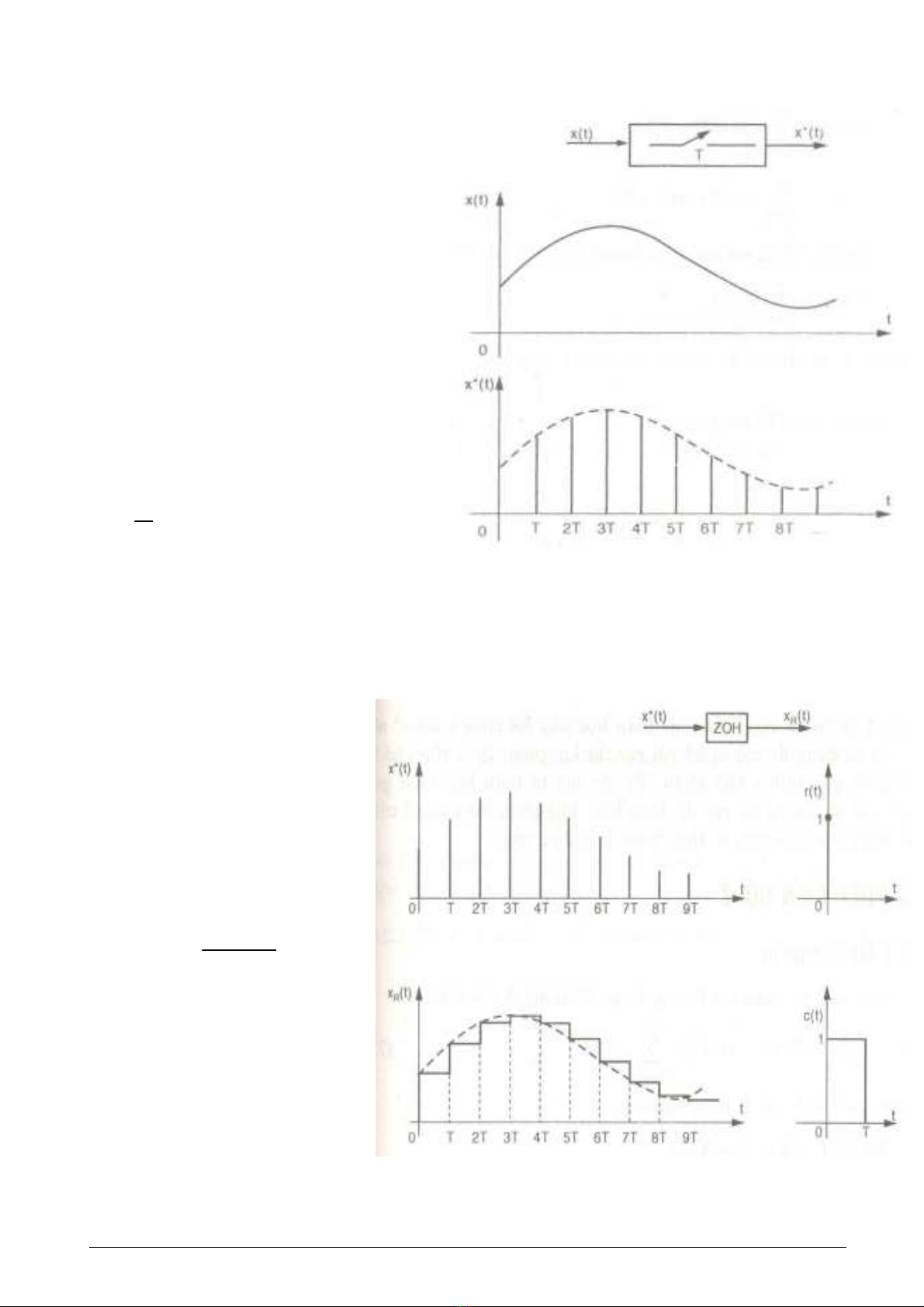
7.1.2 Ñaëc ñieåm laáy maãu
• Laáy maãu laø bieán ñoåi tín hieäu lieân
tuïc theo thôøi gian → tín hieäu rôøi raïc
theo thôøi gian
• Bieåu thöùc toaùn hoïc moâ taû quaù
trình laáy maãu
*
0
() ( ) kTs
k
Xs xkTe
+∞ −
=
=∑ (7.4)
• Ñònh lyù Shanon : Ñeå coù theå phuïc
hoài döõ lieäu sau khi laáy maãu maø
khoâng bò meùo daïng thì taàn soá laáy
maãu phaûi thoûa ñieàu kieän :
12c
ff
T
=≥
c
f
: taàn soá caét cuûa tín hieäu caàn laáy maãu
• Khaâu A/D töông ñöông khaâu laáy maãu (boû qua sai soá löôïng töû)
7.1.3 Khaâu giöõ döõ lieäu
• Chuyeån tín hieäu rôøi raïc
→ tín hieäu lieân tuïc
• Khaâu giöõ baäc 0 ZOH –
Zero-Order Hold : giöõ tín
hieäu baèng haèng soá trong
thôøi gian giöõa 2 laàn laáy maãu
• Haøm truyeàn ZOH :
1
()
Ts
ZOH
e
Gs
s
−
−
= (7.6)
• Khaâu D/A töông ñöông
khaâu ZOH
C7. Moâ Taû Toaùn Hoïc Heä Thoáng ÑK Rôøi Raïc 4
7.2 Pheùp Bieán Ñoåi Z
• Muïc ñích loaïi boû caùc haøm
x
e
7.2.1 Ñònh nghóa
Cho ()xk laø chuoãi tín hieäu rôøi raïc. Bieán ñoåi Z cuûa ()xk laø :
{}
() () () k
k
X z xk xkz
+∞
−
=−∞
==
∑
Z (7.7)
Vôùi Ts
ze=, kyù hieäu : () ()xk X z↔
Z
• Neáu () 0, 0xk k=∀<
thì (7.7) trôû thaønh :
{}
0
() () () k
k
Xz xk xkz
+∞
−
=
==
∑
Z
• Mieàn hoäi tuï (Region of Convergence – ROC)
ROC : taäp hôïp taát caû caùc giaù trò z sao cho X(z) höõu haïn
• Pheùp bieán ñoåi Z ngöôïc : k-1
C
1
() X(z)z
2
xk dz
j
π
=∫
C : ñöôøng cong kín baát kyø naèm trong mieàn hoäi tuï ROC cuûa X(z) vaø bao goác
toïa ñoä
7.2.2 Tính chaát cuûa pheùp bieán ñoåi Z
1. Tính tuyeán tính :
Neáu : 11
() ()xk X z
↔
Z
, 22
() ()xk X z
↔
Z
Thì : 11 2 2 1 1 2 2
() () () ()ax k a x k aX z a X z++
↔
Z
2. Tính dôøi trong mieàn thôøi gian :
Neáu : () ()xk X z
↔
,
thì : 0
0
() ()
k
xk k z X z
−
−↔
Z
• Löu yù : nhaân 0
k
z
−töông öùng laøm
treã tín hieäu 0
k chu kyø laáy maãu
• 1
z
−: toaùn töû laøm treã 1 chu kyø
C7. Moâ Taû Toaùn Hoïc Heä Thoáng ÑK Rôøi Raïc 5
3. Tính tæ leä :
Neáu : () ()xk X z
↔
, thì : 1
() ( )
k
axk Xa z
−
↔
Z
4. Tính ñaïo haøm :
Neáu : () ()xk X z
↔
, thì : ()
() dX z
kx k z dz
−
↔
Z
5. Ñònh lyù giaù trò ñaàu :
Neáu : () ()xk X z
↔
, thì : (0) lim ( )
z
xXz
→∞
=
6. Ñònh lyù giaù trò cuoái :
Neáu : () ()xk X z
↔
, thì : 1
1
() lim(1 ) ()
z
xzXz
−
→
∞= −
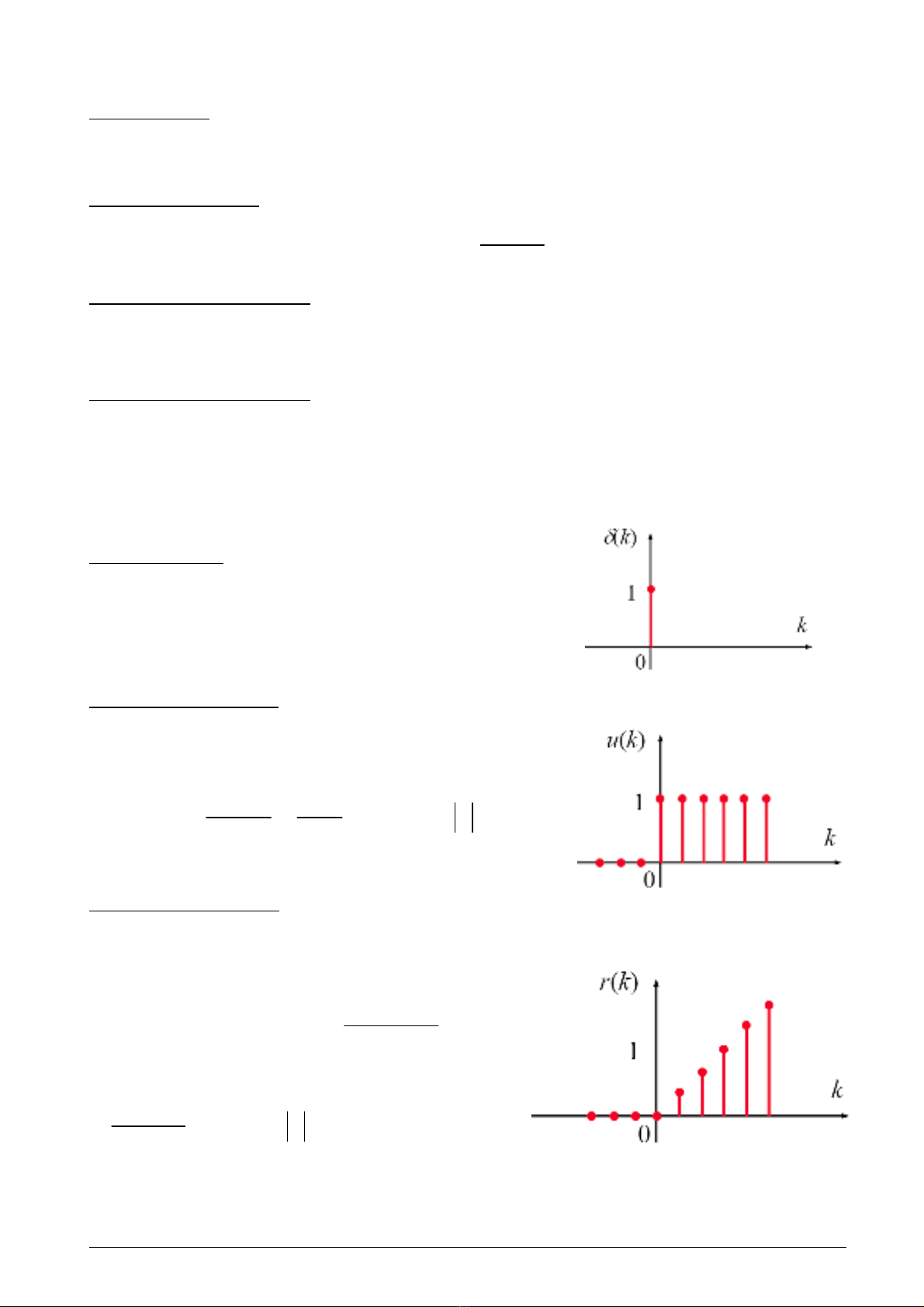
7.2.3 Bieán ñoåi Z cuûa caùc haøm cô baûn
1. Haøm dirac :
10
() 00
k
kk
δ
=
⎧
=⎨≠
⎩
{
}
() 1k
δ
=
Z
2. Haøm naác ñôn vò :
10
() 00
k
uk k
≥
⎧
=⎨<
⎩
{}
1
1
() 1
1
z
uk z
z−
==
−
−
Z (ROC : 1z> )
3. Haøm doác ñôn vò :
0
() 00
kT k
rk k
≥
⎧
=⎨<
⎩
{} { }
1
12
() () (1 )
Tz
rk kTuk z
−
−
==
−
ZZ
2
(1)
Tz
z
=− , (ROC: 1z>)