Chuyên đ BD HSG 12: Sóng c h c và ph ng án thí nghi mề ơ ọ ươ ệ 2010 - 2011
CHUYÊN Đ B I D NG HSG LÝỀ Ồ ƯỠ
M T S BÀI TOÁN V SÓNG CỘ Ố Ề Ơ
I. TÓM T T LÝ THUY T:Ắ Ế
A. Đ I C NG V SÓNG C :Ạ ƯƠ Ề Ơ
1. Ph ng trình sóng t i đi m O là ươ ạ ể uO = Acos(ωt + ϕ)
* Ph ng trình sóng t i đi m M cách O m t đo n x trên ph ng truy n sóng.ươ ạ ể ộ ạ ươ ề
** N u Sóng truy n theo chi u d ng c a tr c Ox thì ế ề ề ươ ủ ụ
uM = AMcos(ωt + ϕ -
x
v
ω
) = AMcos(ωt + ϕ -
2x
πλ
)
** N u Sóng truy n theo chi u âm c a tr c Ox thì ế ề ề ủ ụ
uM = AMcos(ωt + ϕ +
x
v
ω
) = AMcos(ωt + ϕ +
2x
πλ
)
2. Đ l ch pha gi a hai đi m cách ngu n m t kho ng xộ ệ ữ ể ồ ộ ả 1, x2 là
1 2 1 2
2
x x x x
v
ϕ ω π λ
− −
∆ = =
** N u 2 đi m đó n m trên m t ph ng truy n sóng và cách nhau m t kho ng x thì:ế ể ằ ộ ươ ề ộ ả
2
x x
v
ϕ ω π λ
∆ = =
L u ý: ưĐ n v c a x, xơ ị ủ 1, x2,
λ
và v ph i t ng ng v i nhau ( cùng h đ n v )ả ươ ứ ớ ệ ơ ị
3. Trong hi n t ng truy n sóng trên s i dâyệ ượ ề ợ , dây đ c kích thích dao đ ng b i nam châm đi n ượ ộ ở ệ v i t nớ ầ
s dòng đi n là fố ệ thì t n s dao đ ng c a dây là 2fầ ố ộ ủ .
B. SÓNG D NGỪ
1. M t s chú ý: ộ ố
* Đ u c đ nh ho c đ u dao đ ng nh là nút sóng.ầ ố ị ặ ầ ộ ỏ Đ u t do là b ng sóngầ ự ụ
* Hai đi m đ i x ng v i nhau qua nút sóng luôn dao đ ng ng c pha.ể ố ứ ớ ộ ượ
* Hai đi m đ i x ng v i nhau qua b ng sóng luôn dao đ ng cùng pha.ể ố ứ ớ ụ ộ
* Các đi m trên dây đ u dao đ ng v i biên đ không đ i ể ề ộ ớ ộ ổ ⇒ năng l ng không truy n điượ ề
* Kho ng th i gian gi a hai l n s i dây căng ngang (các ph n t đi qua VTCB) là n a chu kỳ.ả ờ ữ ầ ợ ầ ử ử
2. Đi u ki n đ có sóng d ng trên s i dây dài ề ệ ể ừ ợ l:
* Hai đ u là nút sóng: ầ
*
( )
2
l k k N
λ
= ∈
V i : + S b ng sóng = s bó sóng = k và S nút sóng = k + 1ớ ố ụ ố ố
* M t đ u là nút sóng còn m t đ u là b ng sóng: ộ ầ ộ ầ ụ
(2 1) ( )
4
l k k N
λ
= + ∈
V i : + S bó sóng nguyên = k và S b ng sóng = s nút sóng = k + 1ớ ố ố ụ ố
3. Ph ng trình sóng d ng trên s i dây CBươ ừ ợ (v i đ u C c đ nh ho c dao đ ng nh là nút sóngớ ầ ố ị ặ ộ ỏ )
* Đ u B c đ nh (nút sóng):ầ ố ị
** Ph ng trình sóng t i và sóng ph n x t i B: ươ ớ ả ạ ạ
os2
B
u Ac ft
π
=
và
' os2 os(2 )
B
u Ac ft Ac ft
π π π
= − = −
** Ph ng trình sóng t i và sóng ph n x t i M cách B m t kho ng d l n l t làươ ớ ả ạ ạ ộ ả ầ ượ
Trang 1/17
Chuyên đ BD HSG 12: Sóng c h c và ph ng án thí nghi mề ơ ọ ươ ệ 2010 - 2011
và
' os(2 2 )
M
d
u Ac ft
π π π
λ
= − −
** Ph ng trình sóng d ng t i M: ươ ừ ạ
'
M M M
u u u= +
=
2 os(2 ) os(2 )
2 2
d
Ac c ft
π π
π π
λ
+ −
⇒
2 sin(2 ) os(2 )
2
M
d
u A c ft
π
π π
λ
= +
**Biên đ dao đ ng c a ph n t t i M: ộ ộ ủ ầ ử ạ
2 os(2 ) 2 sin(2 )
2
M
d d
A A c A
π
π π
λ λ
= + =
* Đ u B t do (b ng sóng):ầ ự ụ
**Ph ng trình sóng t i và sóng ph n x t i B: ươ ớ ả ạ ạ
' os2
B B
u u Ac ft
π
= =
**Ph ng trình sóng t i và sóng ph n x t i M cách B m t kho ng d là:ươ ớ ả ạ ạ ộ ả
và
' os(2 2 )
M
d
u Ac ft
π π λ
= −
**Ph ng trình sóng d ng t i M: ươ ừ ạ
'
M M M
u u u= +
⇒
2 os(2 ) os(2 )
M
d
u Ac c ft
π π
λ
=
**Biên đ dao đ ng c a ph n t t i M: ộ ộ ủ ầ ử ạ
2 cos(2 )
M
d
A A
πλ
=
L u ý: ư* V i x là kho ng cách t M đ n đ u nút sóng thì biên đ : ớ ả ừ ế ầ ộ
2 sin(2 )
M
x
A A
πλ
=
* V i x là kho ng cách t M đ n đ u b ng sóng thì biên đ : ớ ả ừ ế ầ ụ ộ
2 cos(2 )
M
d
A A
πλ
=
C. GIAO THOA SÓNG
Giao thoa c a hai sóng phát ra t hai ngu n sóng k t h p Sủ ừ ồ ế ợ 1, S2 cách nhau m t kho ng ộ ả l:
Xét đi m M cách hai ngu n l n l t dể ồ ầ ượ 1, d2
* Ph ng trình sóng t i 2 ngu n ươ ạ ồ
1 1
Acos(2 )u ft
π ϕ
= +
và
2 2
Acos(2 )u ft
π ϕ
= +
* Ph ng trình sóng t i M do hai sóng t hai ngu n truy n t i:ươ ạ ừ ồ ề ớ
1
1 1
Acos(2 2 )
M
d
u ft
π π ϕ
λ
= − +
và
2
2 2
Acos(2 2 )
M
d
u ft
π π ϕ
λ
= − +
* Ph ng trình sóng t ng h p t i M: ươ ổ ợ ạ uM = u1M + u2M
1 2 1 2 1 2
2 os os 2
2 2
M
d d d d
u Ac c ft
ϕ ϕϕ
π π π
λ λ
− + +∆
= + − +
** Biên đ dao đ ng t i M: ộ ộ ạ
1 2
2 os 2
M
d d
A A c
ϕ
πλ
− ∆
= +
÷
v i ớ
1 2
ϕ ϕ ϕ
∆ = −
Chú ý: **S c c đ i: ố ự ạ
(k Z)
2 2
l l
k
ϕ ϕ
λ π λ π
∆ ∆
− + < < + + ∈
** S c c ti u: ố ự ể
1 1 (k Z)
2 2 2 2
l l
k
ϕ ϕ
λ π λ π
∆ ∆
− − + < < + − + ∈
1. Khi Hai ngu n dao đ ng cùng pha (ồ ộ
1 2
0
ϕ ϕ ϕ
∆ = − =
)
* Đi m dao đ ng c c đ i có hi u đ ng đi : dể ộ ự ạ ệ ườ 1 – d2 = kλ (k∈Z)
* S đ ng ho c s đi m (ố ườ ặ ố ể không tính hai ngu nồ):
l l
k
λ λ
− < <
** Đi m dao đ ng c c ti u (không dao đ ng): dể ộ ự ể ộ 1 – d2 = (2k+1)
2
λ
(k∈Z)
Trang 2/17
Chuyên đ BD HSG 12: Sóng c h c và ph ng án thí nghi mề ơ ọ ươ ệ 2010 - 2011
** S đ ng ho c s đi m (ố ườ ặ ố ể không tính hai ngu nồ):
1 1
2 2
l l
k
λ λ
− − < < −
2. Khi Hai ngu n dao đ ng ng c pha :(ồ ộ ượ
1 2
ϕ ϕ ϕ π
∆ = − =
)
* Đi m dao đ ng c c đ i: dể ộ ự ạ 1 – d2 = (2k+1)
2
λ
(k∈Z)
*S đ ng ho c s đi m (ố ườ ặ ố ể không tính hai ngu nồ):
1 1
2 2
l l
k
λ λ
− − < < −
** Đi m dao đ ng c c ti u (không dao đ ng): dể ộ ự ể ộ 1 – d2 = kλ (k∈Z)
** S đ ng ho c s đi m (ố ườ ặ ố ể không tính hai ngu nồ):
l l
k
λ λ
− < <
Chú ý: V i bài toán tìm s đ ng dao đ ng c c đ i và không dao đ ng gi a hai đi m M, N cách hai ngu nớ ố ườ ộ ự ạ ộ ữ ể ồ
l n l t là dầ ượ 1M, d2M, d1N, d2N. Đ t ặ∆dM = d1M - d2M ; ∆dN = d1N - d2N và gi s ả ử ∆dM < ∆dN.
+ Hai ngu n dao đ ng cùng pha: ** S c c đ i: ồ ộ ố ự ạ ∆dM < kλ < ∆dN
** S c c ti u: ố ự ể ∆dM < (k+0,5)λ < ∆dN
+ Hai ngu n dao đ ng ng c pha: ** C c đ i:ồ ộ ượ ự ạ ∆dM < (k+0,5)λ < ∆dN
** S c c ti u: ố ự ể ∆dM < kλ < ∆dN
II. CÁC D NG TOÁN:Ạ
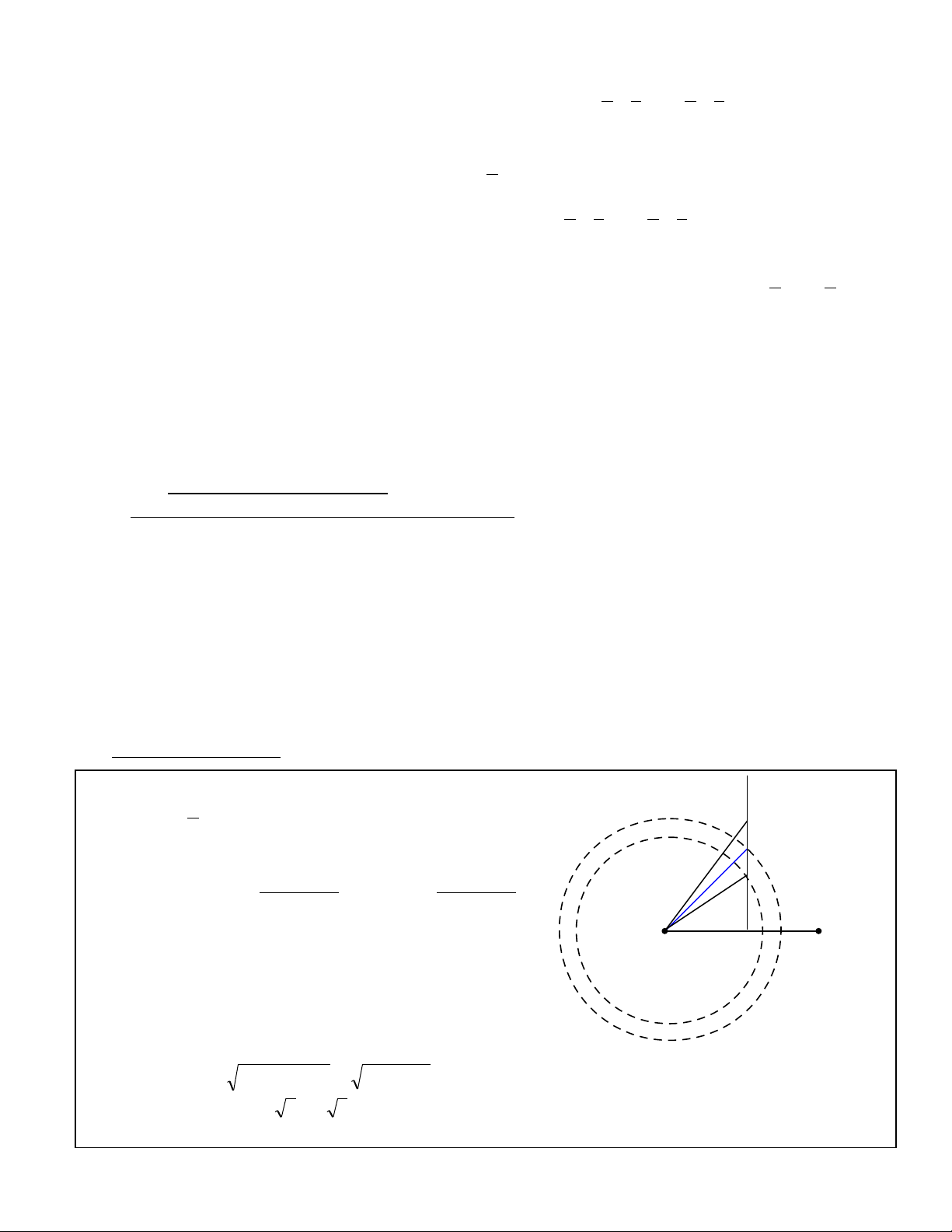
BÀI 1 (T nh Thái Nguyên, Năm h c 2010 - 2011ỉ ọ ): Hai mũi nh n Sọ1, S2 ban đ u cách nhau 8cmầ
g n đ u m t c n rung có t n s f = 100Hz, đ c đ t ch m nh vào m t n c. T c đ truy nắ ở ầ ộ ầ ầ ố ượ ặ ạ ẹ ặ ướ ố ộ ề
sóng trên m t n c là v = 0,8 m/s. ặ ướ
a/ Gõ nh c n rung cho hai đi m Sẹ ầ ể 1, S2 dao đ ng theo ph ng th ng đ ng v i ph ng trìnhộ ươ ẳ ứ ớ ươ
d ng u = A.cos2πft. Vi t ph ng trình dao đ ng c a đi m Mạ ế ươ ộ ủ ể 1 cách đ u Sề1, S2 m t kho ng d = 8cm.ộ ả
b/ Tìm trên đ ng trung tr c c a Sườ ự ủ 1, S2 đi m Mể2 g n Mầ1 nh t và dao đ ng cùng pha v i Mấ ộ ớ 1.
c/ C đ nh t n s rung, thay đ i kho ng cách Số ị ầ ố ổ ả 1S2. Đ l i quan sát đ c hi n t ng giao thoaể ạ ượ ệ ượ
n đ nh trên m t n c, ph i tăng kho ng cách Sổ ị ặ ướ ả ả 1S2 m t đo n ít nh t b ng bao nhiêu ? V i kho ngộ ạ ấ ằ ớ ả
cách y thì gi a Sấ ữ 1, S2 có bao nhiêu đi m có biên đ c c đ i. Coi r ng khi có giao thoa n đ nh thìể ộ ự ạ ằ ổ ị
hai đi m Sể1S2 là hai đi m có biên đ c c ti u.ể ộ ự ể
H NG D N GI IƯỚ Ẫ Ả
a. + λ =
f
v
= 0,8cm và d1 = d2 = d = 8cm
+ Ta có phương trình dao đ ngộ sóng t ngổ h pợ t iạ M1
uM1 = 2A cos
λ
+π
−π
λ
−π )dd(
t200cos
)dd( 2112
v i dớ1 + d2 = 16cm = 20λ và d2 – d1 = 0,
ta đ c: uượ M1 = 2Acos(200πt - 20π)
b. Hai đi m Mể2 và M2’ g n Mầ1 ta có:
S1M2 = d + λ = 8 + 0,8 = 8,8 cm
S1M2’ = d – λ = 8 – 0,8 = 7,2 cm
Do đó: IM2 =
)cm(84,748,8ISMS 222
1
2
21 =−=−
IM1 = S1I
)cm(93,6343 ==
Suy ra M1M2 = 7,84 – 6,93 = 0,91 (cm)
Trang 3/17
M1
M2'
M2
S1I
Chuyên đ BD HSG 12: Sóng c h c và ph ng án thí nghi mề ơ ọ ươ ệ 2010 - 2011
T ng t : IMươ ự 2’ =
'2 2 2 2
1 2 1
S M S I 7, 2 4 5,99(cm)− = − =
M1M2’ = 6,93 – 5,99 = 0,94 (cm)
c. Khi h sóng đã n đ nh thì hai đi m Sệ ổ ị ể 1, S2 là hai tiêu đi m c a các hypecbol và r t g n chúngể ủ ở ấ ầ
xem g n đúng là đ ng yên, còn trung đi m I c a Sầ ứ ể ủ 1S2 luôn n m trên vân giao thoa c c đ i. Do đóằ ự ạ
ta có: S1I = S2I = k
4
)1k2(
42
λ
+=
λ
+
λ
=> S1S2 = 2S1I = (2k + 1)
2
λ
Ban đ u ta đã có: Sầ1S2 = 8cm = 10λ = 20
2
λ
=> ch c n tăng Sỉ ầ 1S2 m t kho ngộ ả
2
λ
= 0,4cm.
Khi đó trên S1S2 có 21 đi m có biên đ c c đ i.ể ộ ự ạ
BÀI 2 (T nh Thanh Hóa, Năm h c 2009 - 2010):ỉ ọ M t sóng c ngang truy n trên m t s i dây r t dàiộ ơ ề ộ ợ ấ
có ph ng trình ươ
( )
xtu
ππ
02,04cos6 −=
; trong đó u và x có đ n v là cm, t có đ n v là giây. Hãy xác đ nhơ ị ơ ị ị
v n t c dao đ ng c a m t đi m trên dây có to đ x = 25 cm t i th i đi m t = 4 s.ậ ố ộ ủ ộ ể ạ ộ ạ ờ ể
H NG D N GI IƯỚ Ẫ Ả
V n t c dao đ ng c a m t đi m trên dây đ c xác đ nh là:ậ ố ộ ủ ộ ể ượ ị
( )
)/(02,04sin24' scmxtuv
πππ
−−==
Thay x = 25 cm và t = 4 s vào ta đ c : ượ
( ) ( )
scmv /245,016sin24
ππππ
=−−=
BÀI 3 (Tp HCM, Năm h c 2010 - 2011ọ): Ba đi m O, A, B cùng n m trên m t n a đ ng th ngể ằ ộ ữ ườ ẳ
xu t phát t O. T i O d t m t ngu n đi m phát sóng âm d ng h ng ra không gian. Không gian xungấ ừ ạ ặ ộ ồ ể ẳ ướ
quanh là m t môi tr ng không h p th âm. M c c ng đ âm t i A là ộ ườ ấ ụ ứ ườ ộ ạ 60 dB, t i B là ạ40 dB. Cho bi tế
c ng đ âm t i m t đi m trong không gian t l ngh ch v i bình ph ng kho ng cách t đi m đó đ n O.ườ ộ ạ ộ ể ỉ ệ ị ớ ươ ả ừ ể ế
Tìm m c c ng đ âm t i trung đi m M c a đo n AB.ứ ườ ộ ạ ể ủ ạ
BÀI 4 (T nh Thanh Hóa, Năm h c 2010 - 2011):ỉ ọ Trong thí nghi m giao thoa sóng m t n c,ệ ặ ướ
hai ngu n k t h p Sồ ế ợ 1, S2 cách nhau 8cm dao đ ng cùng pha v i t n s f = 20Hz. T i đi m M trênộ ớ ầ ố ạ ể
m t n c cách Sặ ướ 1, S2 l n l t nh ng kho ng dầ ượ ữ ả 1 = 25cm, d2 = 20,5cm dao đ ng v i biên đ c c đ i,ộ ớ ộ ự ạ
gi a M và đ ng trung tr c c a AB có hai dãy c c đ i khác.ữ ườ ự ủ ự ạ
a. Tính t c đ truy n sóng trên m t n c.ố ộ ề ặ ướ
b. N là m t đi m thu c đ ng trung tr c c a đo n th ng Sộ ể ộ ườ ự ủ ạ ẳ 1S2 dao đ ng ng c pha v i hai ngu n.ộ ượ ớ ồ
Tìm kho ng cách nh nh t t N đ n đo n th ng n i Sả ỏ ấ ừ ế ạ ẳ ố 1S2.
c. Đi m C cách Sể1 kho ng L th a mãn CSả ỏ 1 vuông góc v i Sớ1S2. Tính giá tr c c đ i c a L đ đi mị ự ạ ủ ể ể
C dao đ ng v i biên đ c c đ i.ộ ớ ộ ự ạ
H NG D N GI IƯỚ Ẫ Ả
a. Tính t c đ truy n sóng:ố ộ ề • T i M sóng có biên đ c c nên: dạ ộ ự 1 – d2 = kλ
k
dd 21 −
=⇒
λ
- Gi a M và trung tr c c a AB có hai dãy c c đ i khác ữ ự ủ ự ạ
3
=⇒
k
• T đó ừ
cm5,1=⇒
λ
, v n t c truy n sóng: v = ậ ố ề λf = 30 cm/s
b. Tìm v trí đi m Nị ể
• Gi s ả ử
tauu
ω
cos
21 ==
, ph ng trình sóng t i N: ươ ạ
λ
π
−ω=
d2
tcosA2u
N
Đ l ch pha gi a ph ng trình sóng t i N và t i ngu n: ộ ệ ữ ươ ạ ạ ồ
λ
π
ϕ
d2
=∆
Đ dao đ ng t i N ng c pha v i dao đ ng t i ngu n thì ể ộ ạ ượ ớ ộ ạ ồ
( )
2
12)12(
2
λ
π
λ
π
ϕ
+=⇒+==∆ kdk
d
Trang 4/17
Chuyên đ BD HSG 12: Sóng c h c và ph ng án thí nghi mề ơ ọ ươ ệ 2010 - 2011
• Do d
≥
a/2
( )
2
12
λ
+⇒ k
≥
a/2 ⇒ k
≥
2,16. Đ dểmin thì k=3.
⇒dmin=
cmx
a
x4,3
2min
2
2
min ≈⇒
+
c. Xác đ nh Lịmax
• Đ t i C có c c đ i giao thoa thì: ể ạ ự ạ
2 2
L a L k .+ − = λ
; k =1, 2, 3... và a = S1S2
Khi L càng l n đớngườ CS1 c t các c c đ i giao thoa có b c càng nh (ắ ự ạ ậ ỏ k càng bé), v y ậngứ v iớ
giá tr l n nh t c a L đ t i C có c c đ i là k =1 ị ớ ấ ủ ể ạ ự ạ
• Thay các giá tr đã cho vào bi u th c trên ta nh n đị ể ứ ậ cượ :
cmLLL 6,205,164 maxmax
max
2≈⇒=−+
BÀI 5 (Năm h c 2009 - 2010):ọ C n rung có mũi nh n A ch m vào m t n c v i t n s rung f =ầ ọ ạ ặ ướ ớ ầ ố
100Hz, thì trên m t n c có sóng lan truy n v i kho ng cách gi a 2 ng n sóng liên ti p là 0,5ặ ướ ề ớ ả ữ ọ ế
cm.Chi u sáng m t n c b ng đèn nh p nháy phát ra 25 ch p sáng trong 1s. Trình bày hi n t ngế ặ ướ ằ ấ ớ ệ ươ
quan sát đ c?ượ
H NG D N GI IƯỚ Ẫ Ả - Th i gian gi a hai l n ch p sáng là tờ ữ ầ ớ 0 = 1/25 = 0,04s
- Chu kỳ c a sóng T = 1 / f = 1 / 100 = 0,01sủ
- T đó suy ra từ0 = 4T.
- Ta th y trong kho ng 2 l n ch p sáng tấ ả ầ ớ 0 sóng đã truy n đi m t quãngề ộ
đ ng s = 4ườ λ = 2 cm ⇒các ng n sóng đ i ch cho nhau.ọ ổ ỗ
Nh v y khi có ch p sáng ta có c m giác hình nh sóng không lan truy n trên m t n c ( các ng nư ậ ớ ả ư ề ặ ướ ọ
sóng hình nh đ ng yên ) ư ứ
BÀI 6 (T nh Thái Nguyên, Năm h c 2009 - 2010):ỉ ọ Trên m t n c có hai ngu n sóng n c A và Bặ ướ ồ ướ
cách nhau 16cm đang dao đ ng vuông góc v i m t n c có cùng ph ng trình x = asin50ộ ớ ặ ướ ươ πt (cm). Bi t C làế
m t đi m trên m t n c, thu c đ ng c c ti u, gi a C và đ ng trung tr c c a đo n AB có m t đ ngộ ể ặ ướ ộ ườ ự ể ữ ườ ự ủ ạ ộ ườ
c c đ i. Kho ng cách AC = 17,2cm; BC = 13,6cm.ự ạ ả
a/ Tính b c sóng và v n t c truy n sóng trên m t n c?ướ ậ ố ề ặ ướ
b/ Trên c nh AC có m y đi m dao đ ng v i biên đ c c đ i (không k hai đi m A và C) ? ạ ấ ể ộ ớ ộ ự ạ ể ể
H NG D N GI IƯỚ Ẫ Ả
Trang 5/17