0
MỘT TRĂM BÀI TẬP
HÌNH HỌC LỚP 9.
Phần 1: 50 bài tập cơ bản.
1
Lời nói đầu:
Trong quá trình ôn thi tốt nghiệp cho học sinh lớp 9,chúng ta
đều nhận thấy học sinh rất ngại chứng minh hình học. Cũng do
học sinh còn yếu kiến thức bộ môn.Hơn nữa giáo viên thường
rất bí bài tập nhằm rèn luyện các kỹ năng, đặc biệt là luyện thi
tốt nghiệp.Đồng thời do học sinh chúng ta là học sinh có hoàn
cảnh gia đình còn nghèo vì vậy học sinh yếu kỹ năng vận dụng
nếu chúng ta chỉ chữa một vài bài tập mà thôi.
Do để học sinh có thể chủ động trong quá trình làm bài,các bài
tập trong tài liệu này chỉ có tính cất gợi ý phương án chứng
minh chứ chưa phải là bài giải hoàn hảo nhất.
Bên cạnh đó để có bài tập riêng của từng giáo viên,người giáo
viên cần biết biến đổi bài tập trong tài liệu này sao cho phù hợp
với đối tượng học sinh.
Tài liệu được sưu tầm trong các sách và đã được thống kê trong
phần phụ lục.Cấm việc in sao,sao chép dưới bất kỳ hình thức
nào mà không có sự nhất trí của tác giả.
Dù có nhiều cố gắng song tài liệu chắc chắn kông thể không có
sai soat.Mong được sự góp ý của bạn đọc.Thư về:
2
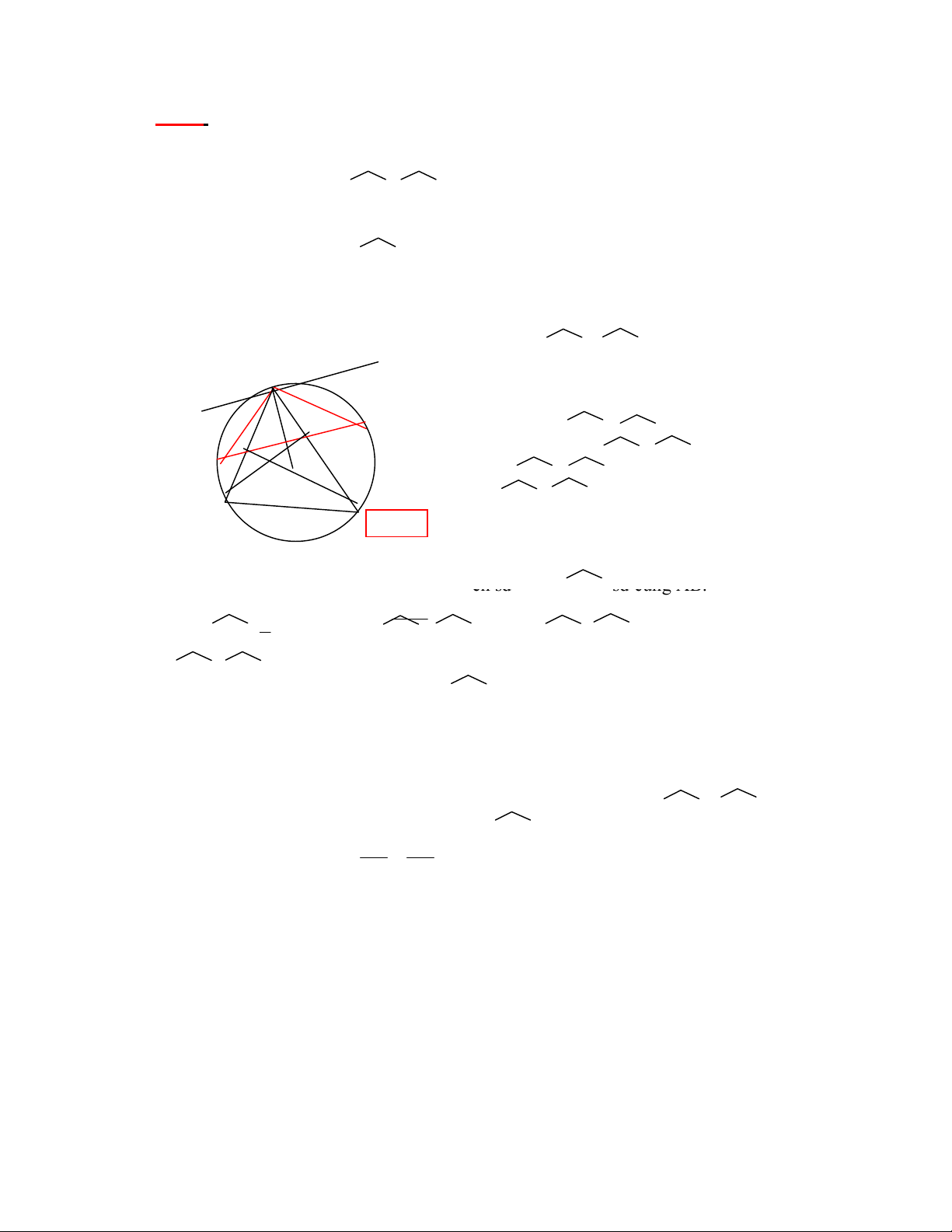
Bài 1: Cho ABC có các đường cao BD và CE.Đường thẳng DE cắt đường tròn
ngoại tiếp tam giác tại hai điểm M và N.
1. Chứng minh:BEDC nội tiếp.
2. Chứng minh: góc DEA=ACB.
3. Chứng minh: DE // với tiếp tuyến tai A của đường tròn ngoại tiếp tam giác.
4. Gọi O là tâm đường tròn ngoại tiếp tam giác ABC.Chứng minh: OA là phân
giác của góc MAN.
5. Chứng tỏ: AM2=AE.AB.
Giợi ý:
y
A
x
N
E D
M O
B C
Ta phải c/m xy//DE.
Do xy là tiếp tuyến,AB là dây cung nên sđ góc xAB=
2
1sđ cung AB.
Mà sđ ACB=
2
1sđ AB. góc xAB=ACB mà góc ACB=AED(cmt)
xAB=AED hay xy//DE.
4.C/m OA là phân giác của góc MAN.
Do xy//DE hay xy//MN mà OAxyOAMN.OA là đường trung trực của
MN.(Đường kính vuông góc với một dây)AMN cân ở A AO là phân giác
của góc MAN.
5.C/m :AM2=AE.AB.
Do AMN cân ở A AM=AN cung AM=cung AN.góc MBA=AMN(Góc
nội tiếp chắn hai cung bằng nhau);góc MAB chung
MAE ฀ BAM
MA
AE
AB
MA MA2=AE.AB.

1.C/m BEDC nội tiếp:
C/m góc BEC=BDE=1v. Hia
điểm D và E cùng làm với hai
đầu đoạn thẳng BC một góc
vuông.
2.C/m góc DEA=ACB.
Do BECD ntDMB+DCB=2v.
Mà DEB+AED=2v
AED=ACB
3.Gọi tiếp tuyến tại A của (O)
là đường thẳng xy (Hình 1)
Hình 1
3
Bài 2:
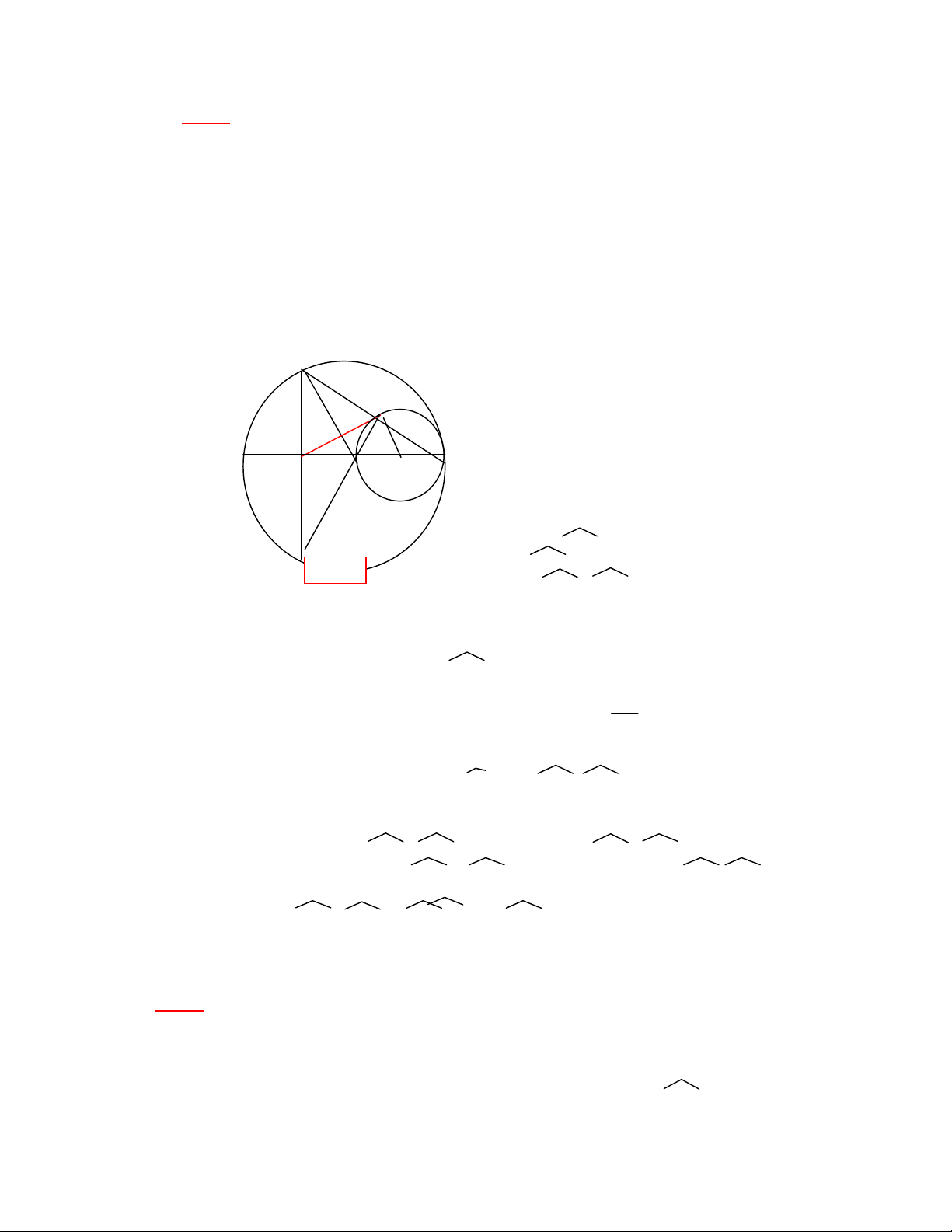
Cho(O) đ?ờg kính AC.trên đạ OC lấ để B và vẽđ?ờg tròn tâm O’, đ?ờg kính
BC.Gọ M là trung để củ đạ AB.TừM vẽdây cung DE vuông góc vớ AB;DC cắ đ?ờg
tròn tâm O’ tạ I.
1.Tứgiác ADBE là hình gì?
2.C/m DMBI nộ tiế.
3.C/m B;I;C thẳg hàng và MI=MD.
4.C/m MC.DB=MI.DC
5.C/m MI là tiế tuyế củ (O’)
Gợ ý:
D
I
A M O B O’ C
E
3.C/m B;I;E thẳg hàng.
Do AEBD là hình thoi BE//AD mà ADDC (góc nộ tiế chắ nử đ?ờg
tròn)BEDC; CMDE(gt).Do góc BIC=1v BIDC.Qua 1 để B có hai đ?ờg
thẳg BI và BE cùng vuông góc vớ DC B;I;E thẳg hàng.
C/m MI=MD: Do M là trung để DE; EID vuông ởIMI là đ?ờg trung tuyế củ
tam giác vuông DEI MI=MD.
4. C/m MC.DB=MI.DC.
hãy chứg minh MCI฀ DCB (góc C chung;BDI=IMB cùng chắ cung MI do
DMBI nộ tiế)
5.C/m MI là tiế tuyế củ (O’)
-Ta có O’IC Cân góc O’IC=O’CI. MBID nộ tiế MIB=MDB (cùng chắ cung
MB) BDE cân ởB góc MDB=MEB .Do MECI nộ tiế góc MEB=MCI (cùng
chắ cung MI)
Từđ suy ra góc O’IC=MIB MIB+BIO’=O’IC+BIO’=1v
Vậ MI O’I tạ I nằ trên đ?ờg tròn (O’) MI là tiế tuyế củ (O’).

Bài 3:
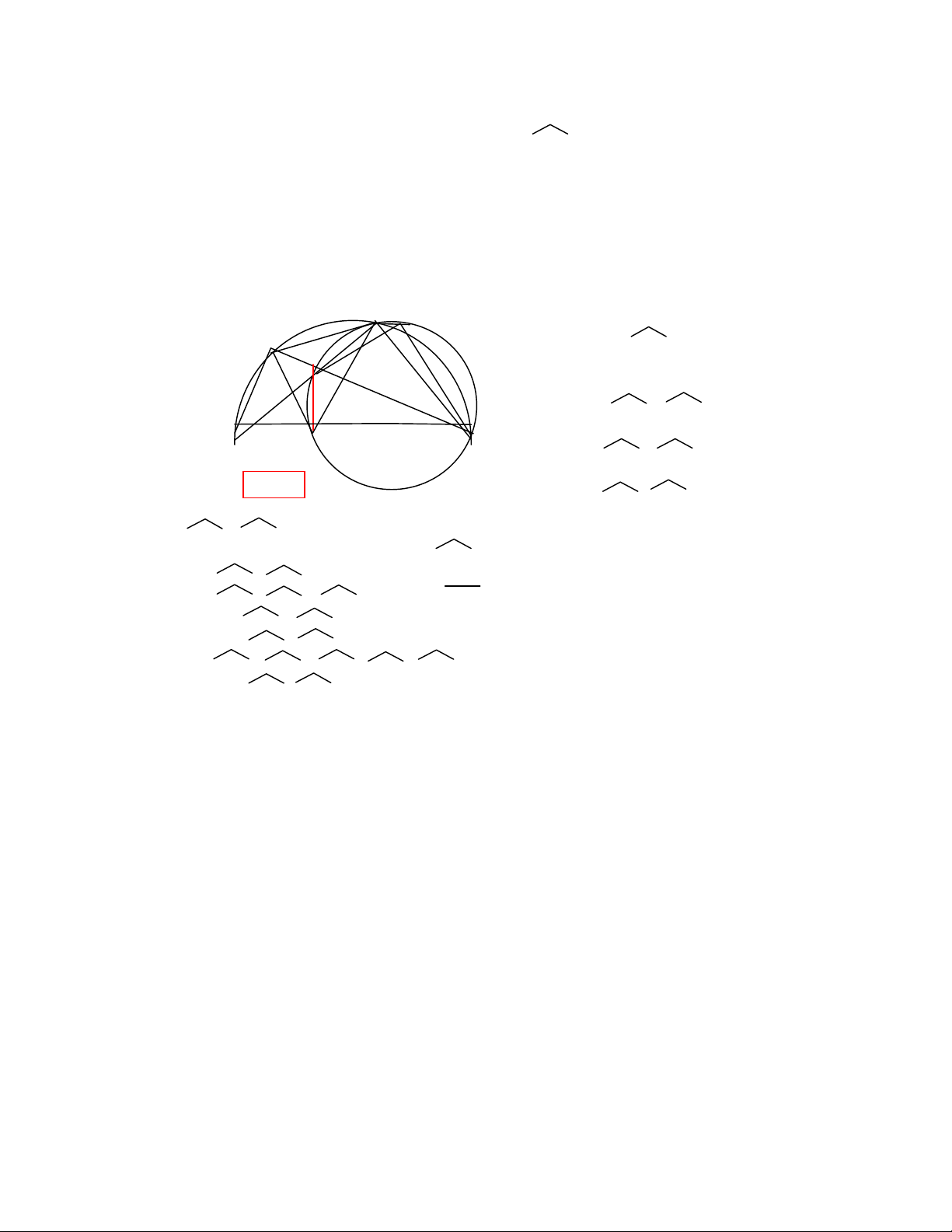
Cho ABC có góc A=1v.Trên AC lấ để M sao cho AM<MC.Vẽđ?ờg tròn tâm
O đ?ờg kính CM;đ?ờg thẳg BM cắ (O) tạ D;AD kéo dài cắ (O) tạ S.
1. C/m BADC nộ tiế.
1.Do MA=MB và AB
DE tạ
M nên ta có DM=ME.
ADBE là hình bình hành.
Mà BD=BE(AB là đ?ờg
trung trự củ DE) vậ ADBE
;là hình thoi.
2.C/m DMBI nộ tiế.
BC là đ?ờg kính,I(O’) nên
Góc BID=1v.Mà góc
DMB=1v(gt)
BID+DMB=2vđcm.
Hình 2
4
2. BC cắ (O) ởE.Cmr:MR là phân giác củ góc AED.
3. C/m CA là phân giác củ góc BCS.
Gợ ý:
D S
A M
O
B E C
AEM=MED.
4.C/m CA là phân giác củ góc BCS.
-Góc ACB=ADB (Cùng chắ cung AB)
-Góc ADB=DMS+DSM (góc ngoài tam giác MDS)
-Mà góc DSM=DCM(Cùng chắ cung MD)
DMS=DCS(Cùng chắ cung DS)
Góc MDS+DSM=SDC+DCM=SCA.
Vậ góc ADB=SCAđcm.

1.C/m ABCD nộ tiế:
C/m A và D cùng làm
vớ hai đ?u đạ thẳg BC
mộ góc vuông..
2.C/m ME là phân giác
củ góc AED.
Hãy c/m AMEB nộ tiế.
Góc ABM=AEM( cùng
chắ cung AM)
Góc ABM=ACD( Cùng
chắ cung MD)
Góc ACD=DME( Cùng
chắ cung MD)
Hình 3