NGÂN HÀNG CÂU H I THI K T THÚC H C PH NỎ Ế Ọ Ầ
LÝ THUY T ĐI U KHI N T Đ NG Ế Ề Ể Ự Ộ (3 TÍN CH )Ỉ
Dùng cho đào t o b c đ i h c theo h c ch tín ch chuyên ngành: S ph m k thu tạ ậ ạ ọ ọ ế ỉ ư ạ ỹ ậ
đi nệ
1. N I DUNG ĐÁNH GIÁ THI K T THÚC H C PH N:Ộ Ế Ọ Ầ Lý thuy t đi u khi n tế ề ể ự
đ ng ộ
2. PH NG PHÁP ĐÁNH GIÁ :ƯƠ V n đáp ho c vi tấ ặ ế
3. NGUYÊN T C T NG H P CÂU H I LÀM Đ THI K T THÚC H C PH NẮ Ổ Ợ Ỏ Ề Ế Ọ Ầ
- Nguyên t c: M t đ t h p t 2 câu h i b t kỳắ ộ ề ổ ợ ừ ỏ ấ
- Thang đi m: 10ể
- Lo i câu h i: lo i 1ạ ỏ ạ
4. NGÂN HÀNG CÂU H IỎ
4.1. Câu h i lo i 1 (5 đi m) – Bài t pỏ ạ ể ậ
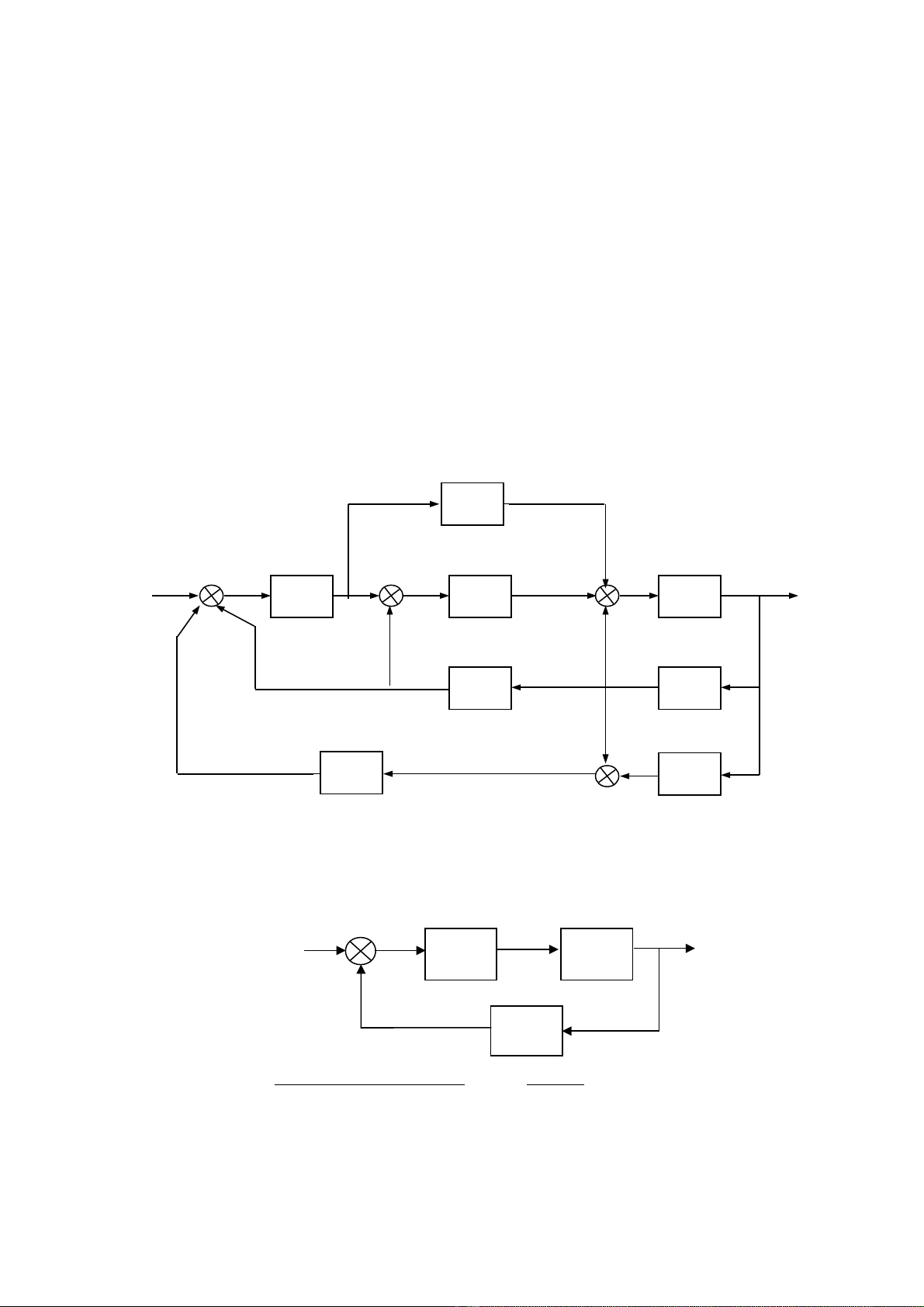
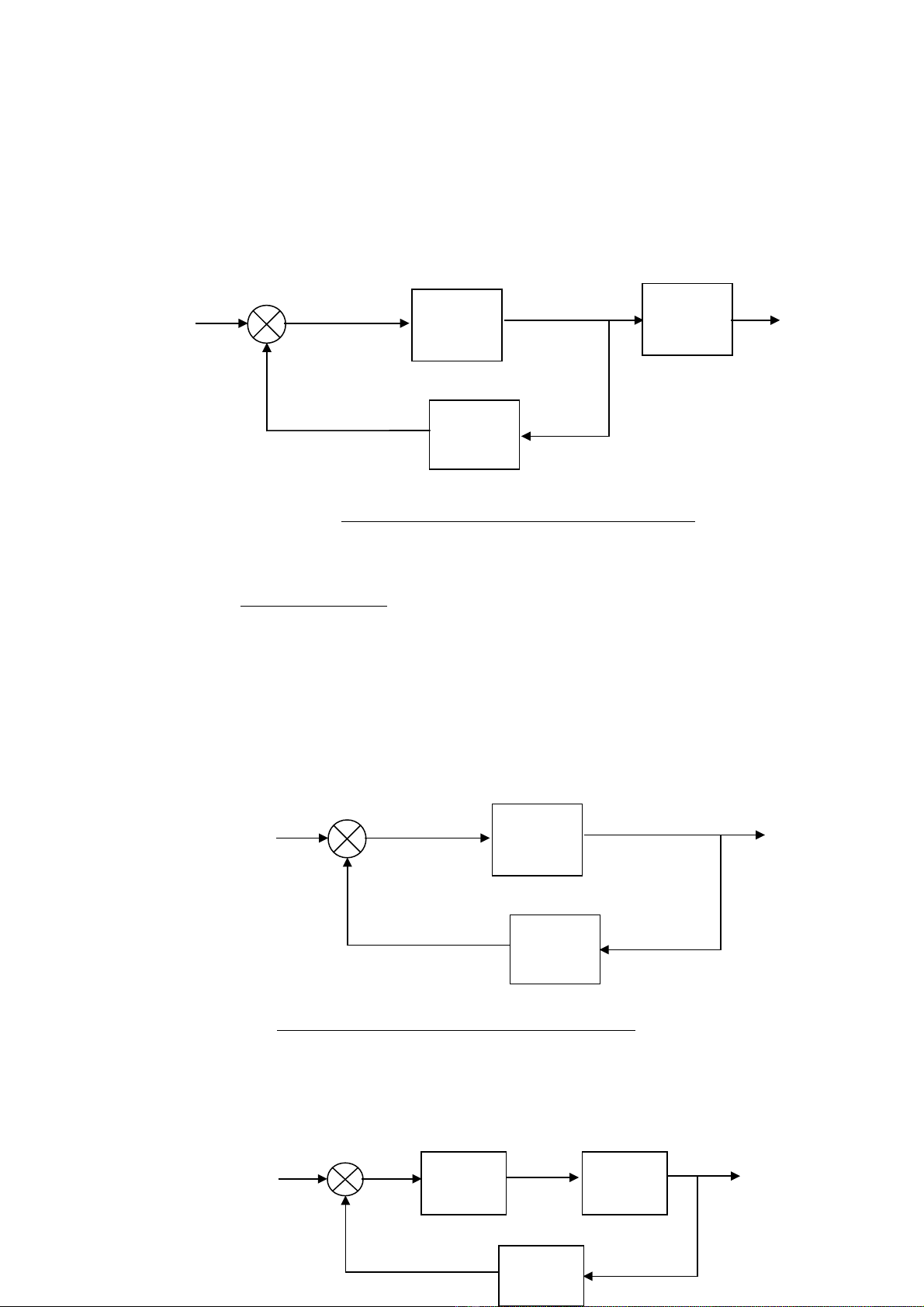
1.Cho h đi u khi n có c u trúcệ ề ể ấ
Hãy xác đ nh hàm truy n cho h theo Wị ề ệ 1÷W8
2. Cho h có c u trúcệ ấ
V i: ớ
10
1(2 1)( 0.1)(3 2)
Wp p p
=+ + +
;
2
5
2( 1)
Wp
=+
;
3 ( 2)W P
= +
Hãy xét n đ nh cho hổ ị ệ
W1 W2
W3
(-)
X(p) Y(p)
W4
W2W3
W1
W6W5
W7
W8
(-) (-) (-) (-)
(-)
(-) Y
X
•
•
•
•
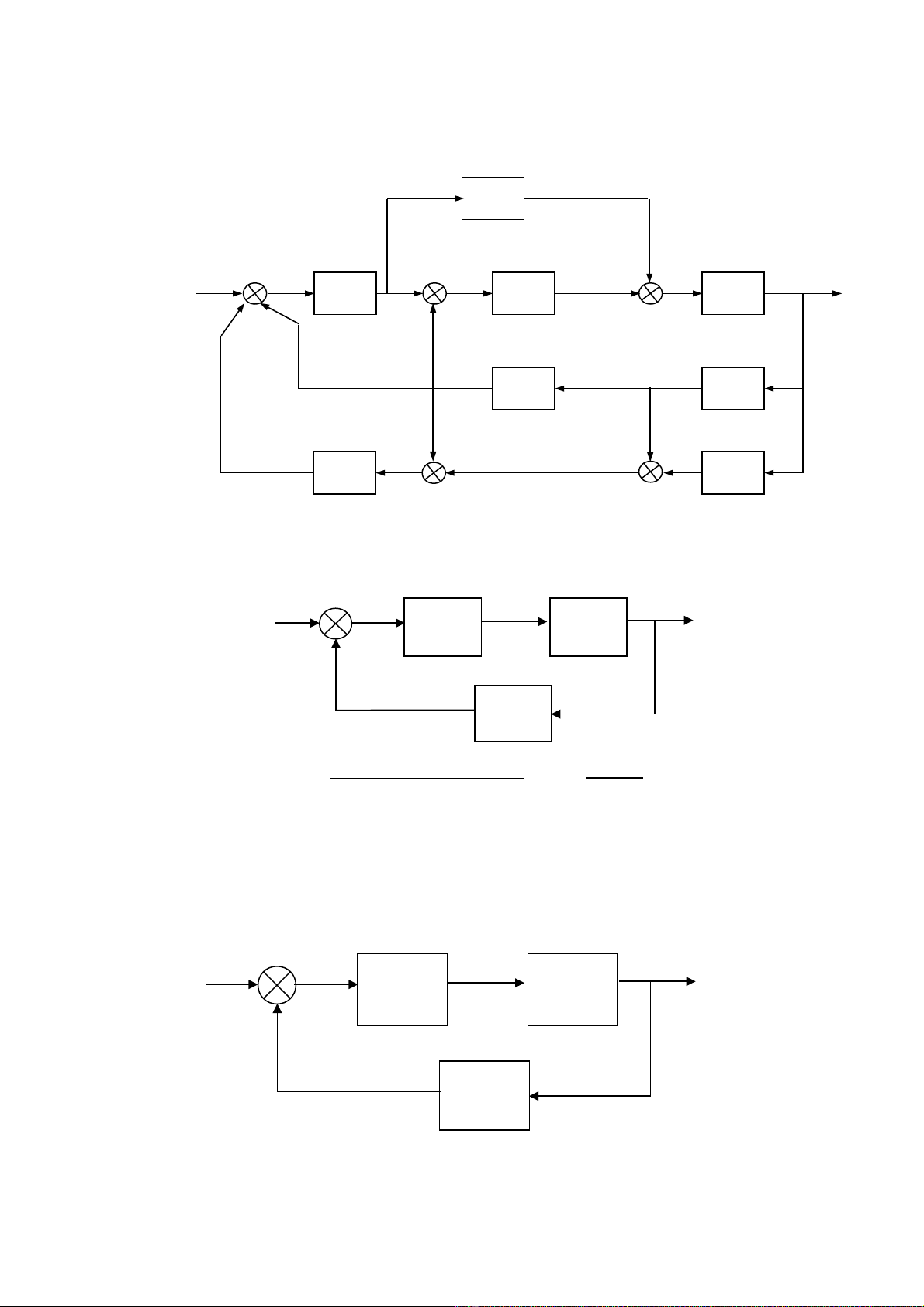
3. Cho h đi u khi n có c u trúcệ ề ể ấ
Hãy xác đ nh hàm truy n cho h theo Wị ề ệ 1÷W8
4. Cho h có c u trúcệ ấ
V i: ớ
10
1(2 5)( 0.1)(3 2)
Wp p p
=+ + +
;
2
10
2( 1)
Wp
=+
;
α=W
3
Hãy xác đ nh ịα đ h n đ nhể ệ ổ ị
5. Cho h có c u trúcệ ấ
W4
W2W3
W1
W6W5
W7
W8
(-) (-)
(-)
(-)
(-)
(-) Y
X
•
•
•
•
W1 W2
W3
(-)
X(p) Y(p)
W1 W2
W3
(-)
U(p) Y(p)
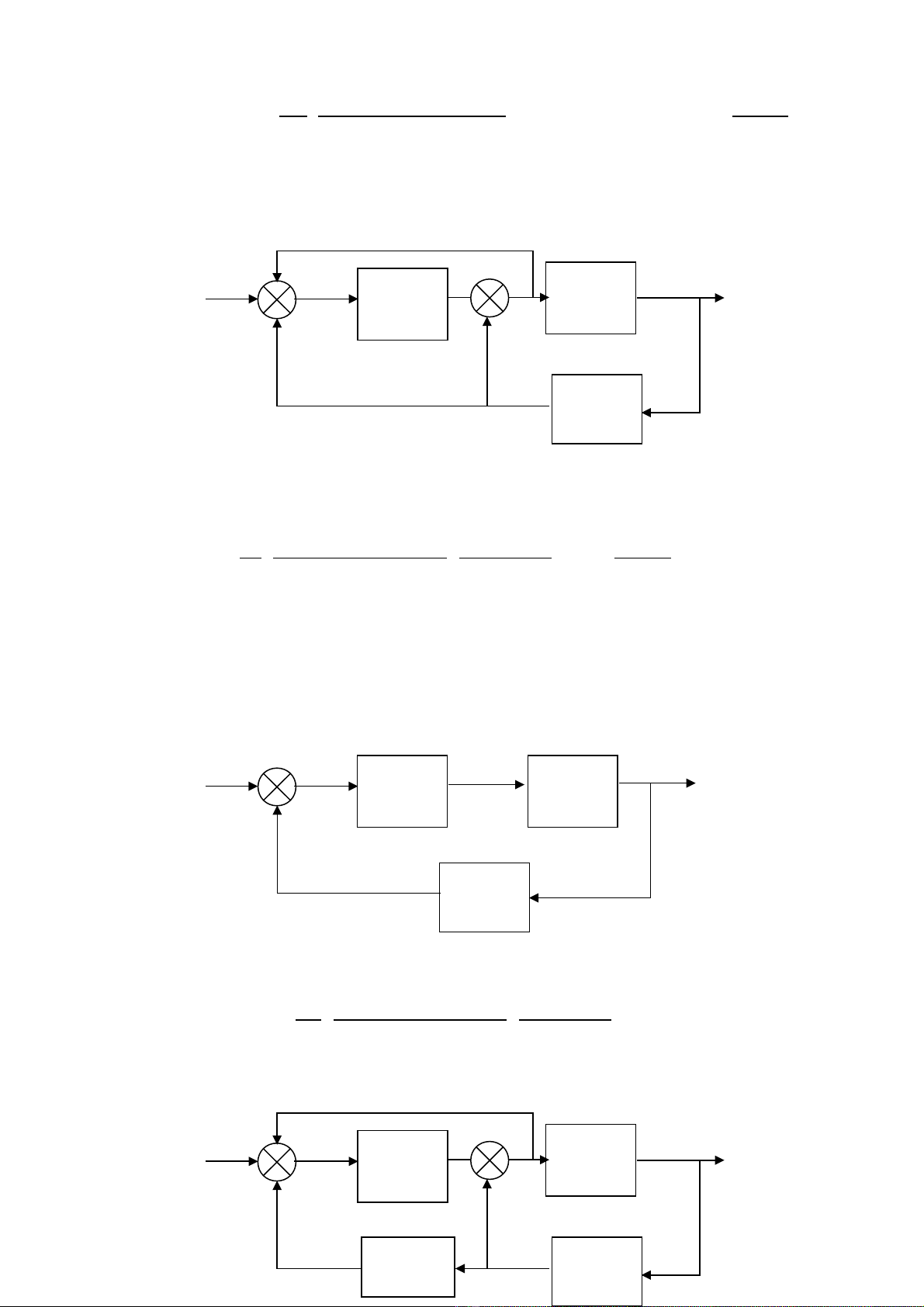
V i: ớ
101.00001.0
10
.
10
1
23
++
=
ppp
W
;
)103,0(1,02
+=
pW
;
1.0
10
3
+
=
p
W
Hãy v LẽH(ω)
6. Cho h có c u trúcệ ấ
V i: ớ
;
2
10
2( 1)
Wp
=+
;
3 0.1W
=
Hãy xét n đ nh cho h và s nghi m c a ph ng trình đ c tính h có ph n th cổ ị ệ ố ệ ủ ươ ặ ệ ầ ự
d ng.ươ
7. Cho h có c u trúcệ ấ
V i: ớ
2 2 2
10 10 100
1(0.01 ) 0.01 1 (0.1 1)
Wp p p p
= × ×
+ + +
;
2 10( 1)W p
= +
;
3 0.1W
=
Hãy v LẽH(ω)
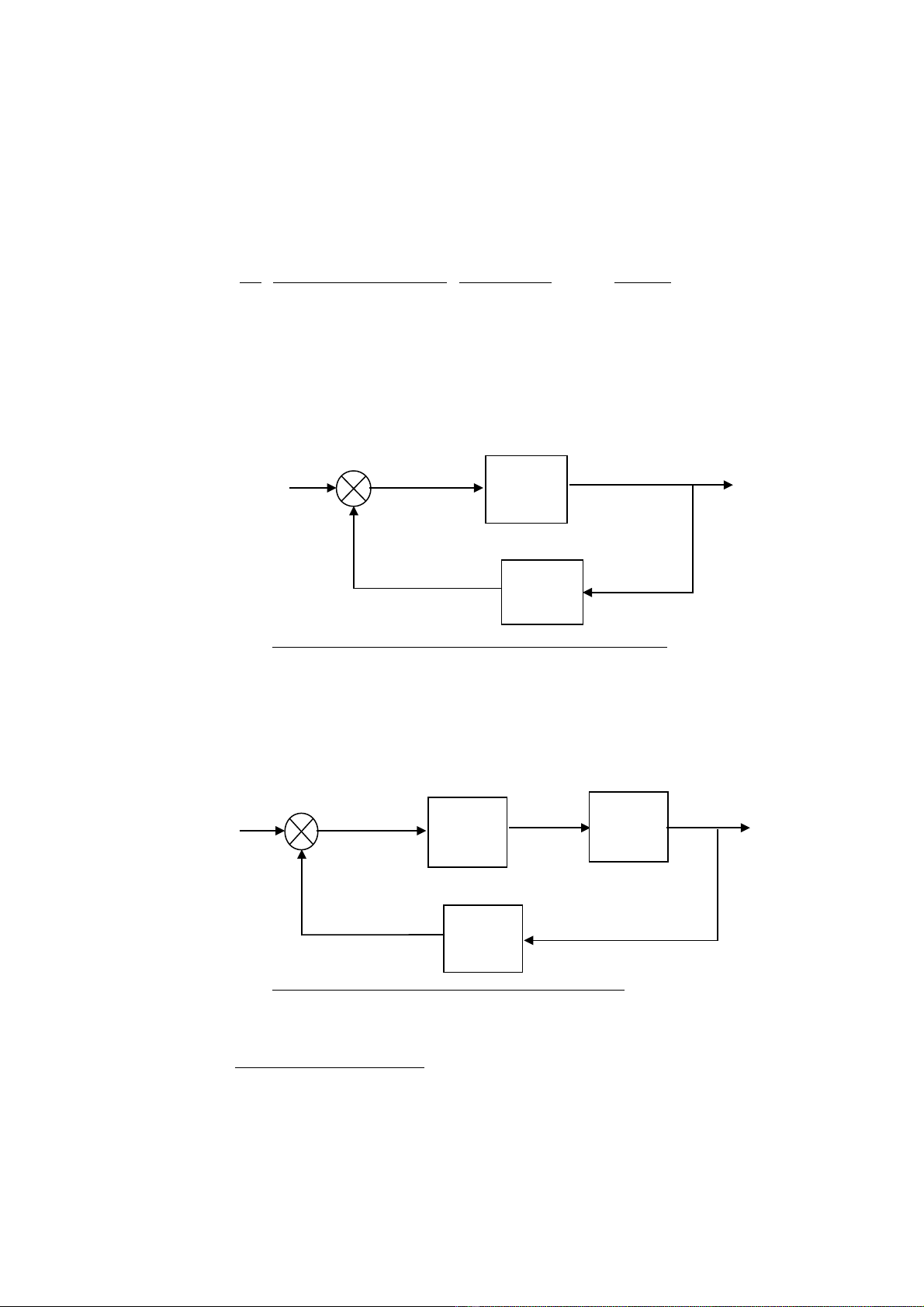
8. Cho h có c u trúcệ ấ
W1 W2
W3
(-)
U(p) Y(p)
(-)
(-)
W1 W2
W3
(-)
U(p) Y(p)
(-)
(-)
W4
W1 W2
W3
(-)
U(p) Y(p)
V i: ớ
;
2
10
2( 1)
Wp
=+
;
3 0.1W
=
; W4=0,2
Hãy xét n đ nh cho h và s nghi m c a ph ng trình đ c tính h có ph n th cổ ị ệ ố ệ ủ ươ ặ ệ ầ ự
d ng.ươ
9. Cho h có c u trúcệ ấ
V i: ớ
12 2
(30 200)
(0.1 1)(0.0002 1) (0,03 1) (0,5 2)
+
=+ + + +
P
Wp p p p P
;
10
2
.=W
Hãy thi t k s đ nguyên lý m ch hi u ch nh.ế ế ơ ồ ạ ệ ỉ
10. Cho h có c u trúcệ ấ
V i: ớ
12 2
100(0.8 2)
(0.1 0.01)(0.002 0.2) (0,03 0.4)
p
Wp p p
+
=+ + +
;
_ 0.45
22
(0.2 1)
( 0.2) (0,01 0.1)
+
=+ +
p
p e
Wp p
;
30.1
=
W
Hãy xác đ nh sai l ch tĩnh St% c a h khi tín hi u vào có d ng:ị ệ ủ ệ ệ ạ
•u(t) = 5.1(t)
W1
W2
(-)
U(p) Y(p)
W1
W3
(-)
U(p) Y(p)
W2
11. Cho h có c u trúcệ ấ
V i: ớ
12 2
100(0.5 1)
(0.1 2)(0.002 1) (0,03 1)
p
Wp p p p
+
=+ + +
;
21W
=
;
)+p,()+p(
e)+p.(
=W
p._
10101
120
2
30
3
Hãy xác đ nh sai l ch tĩnh St% c a h khi tín hi u vào có d ng:ị ệ ủ ệ ệ ạ
•u(t) = 3.1(t)
12. Cho h có c u trúcệ ấ
V i: ớ
2
3 2
10(0,1 1)
1(0.1 0.2 0.4 1)(2 1)(0,6 3)
+
=+ + + + +
P
Wp p p P P
;
2 0.1W
=
Hãy xác đ nh h ph ng trình tr ng thái và tìm các ma tr n A, B, C, D.ị ệ ươ ạ ậ
13. Cho h có c u trúcệ ấ
W1
W2
(-)
U(p) Y(p)
W3
W1
W2
(-)
U(p) Y(p)
W1 W2
W3
(-)
U(p) Y(p)