1
Chương VI. PHÂN TÍCH PHƯƠNG SAI
Phương pháp kiểm định sẽ được mởrộng trong trường hợp so sánh trung bình của nhiều tổng
thể, được xây dựng trong việc xem xét các biến thiên (phương sai) của các giá trịtrong nội bộ
nhóm. Do vậy, phương pháp kiểm định giảthuyết vềsựbằng nhau của trung bình nhiều tổng thể
được gọi chung là phương pháp phân tích phương sai ANOVA.
1. Phân tích phương sai một yếu tố
Phân tích phương sai một yếu tố được sửdụng trong trường hợpchỉcó yếu tố nào đó được xem
xét nhằm xác định ảnh hưởng của nó đến một yếu tốkhác.
Yếu tố được xem xét ảnh hưởng sẽ được dùng để phân loại các quan sát thành các nhóm khác
nhau.
Ví dụ:Một nghiên cứu được thực hiện nhằm xét xem phải chăng yếu tốthu nhập có ảnh hưởng
đến sốtiền chi mua thực phẩm hàng tháng của các gia đình. Như vậy, dựa vào mức thu nhập, các
gia đình sẽ được chia thành các nhóm khác nhau, ghi nhận sốtiền chi mua thực phẩm hàng
tháng, và so sánh sốtiền chi mua thực phẩm hàng tháng trung bình theo các mức thu nhập khác
nhau này.
Nếu yếu tốthu nhập không ảnh hưởng thì trung bình của sốtiền chi mua thực phẩm bằng nhau
của tất cảcác nhóm.
Hay ngược lại, yếu tốthu nhập thực sựcó ảnh hưởng, sốtiền chi mua thực phẩm hàng tháng
trung bình của các gia đình có các mức thu nhập khác nhau sẽkhông bằng nhau.
Tổng quát:
Giảsửta có k- nhóm (mẫu); , ,…, quan sát được chọn ngẫu nhiên độc lập từtổng thể
(, ,…, có thểkhác nhau về kích thước).
Gọi, ,…, là các trung bình tổng thể;
là quan sát thứcủa nhóm thứ.
Bảng các giá trịquan sát của nhóm
Nhóm
1
2
…
k
…
…
….
….
….
….
…
Với giả định các tổng thểphân phối chuẩn, có phương sai bằng nhau, các sai số là độc lập với
nhau, phân tích phương sai một yếu tốthực hiện như sau:
: = =…= ì ô ị ả ưở ở ế ố đ é
: ô ả ấ ả đề ằ (=1,2,…, )
2
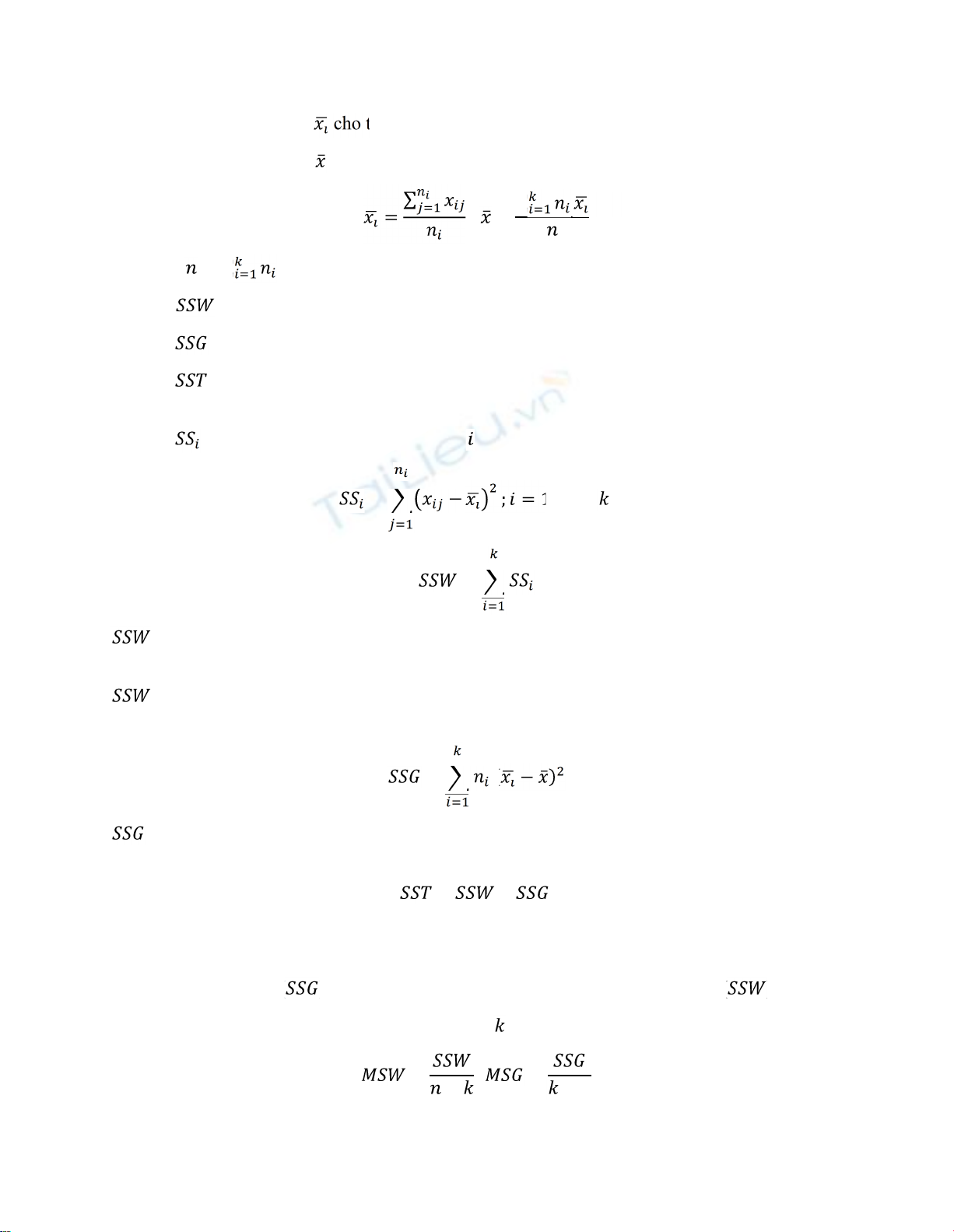
B1. Tính giá trịtrung bình cho từng nhóm;
chung cho tất cảcác nhóm.
=∑; =∑
Trong đó =∑.
B2. Gọi là sựbiến thiên trong nội bộtừng nhóm;
là sựbiến thiên giữa các nhóm;
là tổng bình phương các chênh lệch giữa từng quan sát với trung bình tất cảcác
quan sát;
là sựbiến thiên trong nội bộnhóm .
= − ; =1,2,…, .
=
là tổng bình phương các chênh lệch giữa từng quan sát với trung bình của nhóm mà quan
sát thuộc về.
thểhiện sựbiến thiên do các yếu tốkhác, không do yếu tốnghiên cứu (yếu tố dùng để phân
chia các nhóm).
=(− )
thểhiện sựbiến thiên do sựkhác nhau giữa các nhóm, tức là biến thiên do yếu tốnghiên
cứu (yếu tố dùng để phân chia các nhóm). = + .
Công thức này chính là cơ sở của phương pháp phân tích phương sai một yếu tố:
Biến thiên của các quan sát so với giá trịtrung bình là tổng cộng của biển thiên được giải thích
bởi yếu tốnghiên cứu ( )và biến thiên do các yếu tốkhác, không nghiên cứu( ).
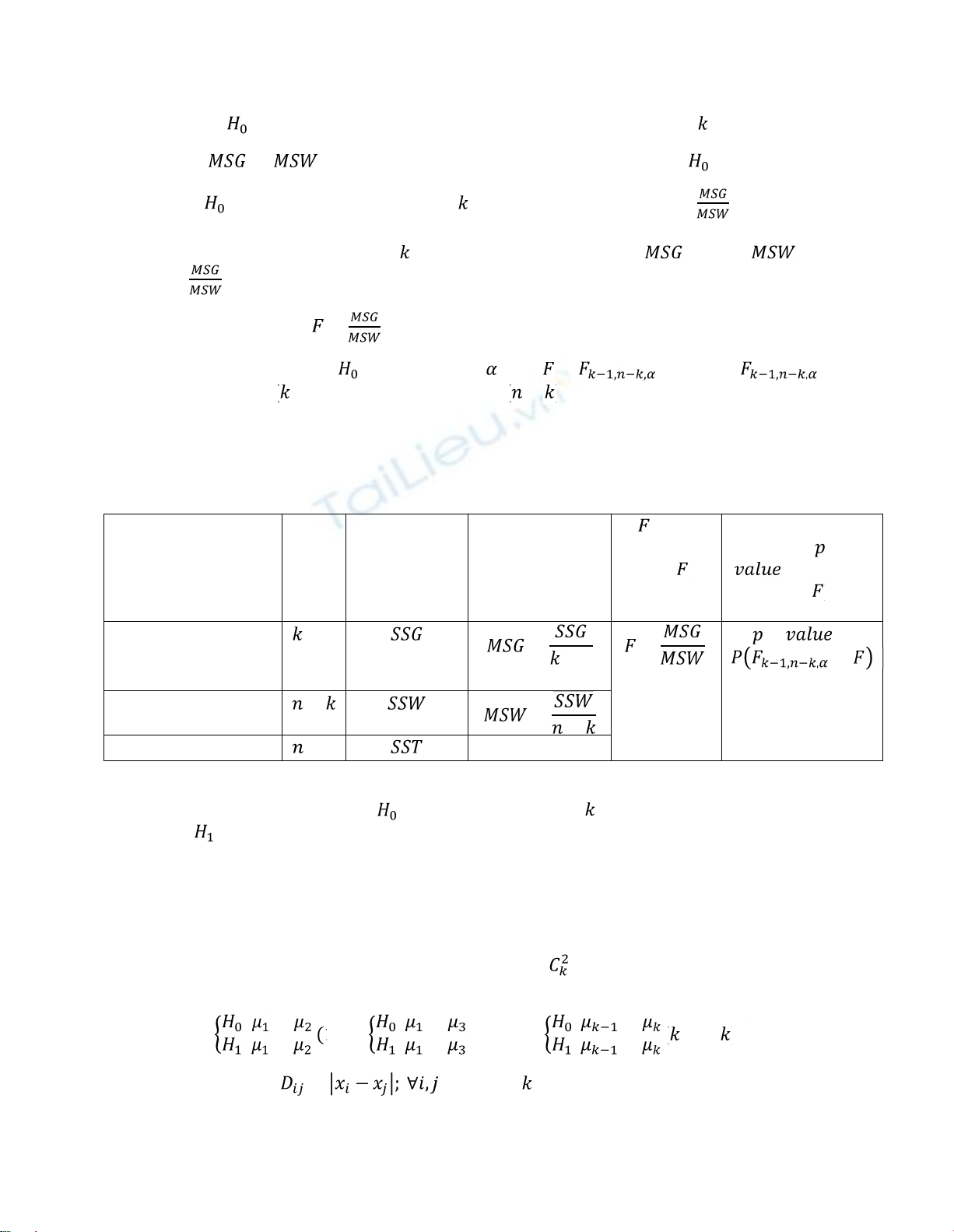
B3. Tính các ước lượng cho phương sai chung của tổng thể
=−; = −1
3
Nếu giảthuyếtđúng, ta có hai giá trị ước lượng cho phương sai chung của tổng thể.
Do đó, tỷ sốvà có thể dùng làm căn cứ để kết luận vềgiảthuyết .
Nếuđúng, nghĩa là trung bình của tổng thểbằng nhau, thì tỷsốsẽgần với giá
trị1.
Ngược lại, khi trung bình của tổng thểkhông bằng nhau thì lớn hơn thì tỷ
sốsẽlớn hơn 1.
B4. Tính giá trịkiểm định =.
Quy tấc quyết định: Bác bỏ ở mức ý nghĩa , nếu>, , ; trong đó , , có
phân phối Fisher với( −1)bậc tựdo của tửsốvà ( − )bậc tựdo của mẫu số.
Bảng phân tích phương sai thường được phân tích bằng máy tính với các phần mềm thông dụng
như Excel, SPSS, Eview dưới dạng bảng sau:
Source (biến thiên)
D. F
(bậc
tựdo)
Sum of
Squares (tổng
các chênh
lệch bình
phương)
Ratio
(giá trịkiểm
định )
F Prob.
(giá trị−
của kiểm
định )
Between Groups
(giữa các nhóm)
−1
=
− =
, , >
Within Groups
(trong nội bộnhóm)
−
Total (tổng)
−1
Vấn đề đặt ra là một khi giảthuyết cho rằng trung bình của tổng thểbằng nhau bịbác bỏthì
chấp nhận . Vậy trung bình của những tổng thểnào thì khác nhau, tổng thểnào có trung bình
lớn hơn hay nhỏ hơn?
Ở đây ta đề cập đến phương pháp Tukey so sánh từng cặp trung bình tổng thểvới nhau.
2. So sánh từng cặp trung bình tổng thể: kiểm định Tukey
Do so sánh từng cặp trung bình tổng thểnên ta có tất cảbài toán kiểm định trung bình tổng
thể như sau: : =
: ≠ (1,2); : =
: ≠ (1,3);…; : =
: ≠ ( −1, )
Tính giá trịkiểm định = − ;∀, =1,2,…,
4
Tiêu chuẩn so sánh
=, ,
Trong đó , , là giá trịtra bảng phân phốiởmức ý nghĩa ;
với bậc tự do tương ứng là và (−);
=min{ ; ;…; }.
Quy tắc quyết định: Bác bỏtrong bài toán (,)ởmức ý nghĩa nếu>.
3. Phân tích phương sai với mẫu ngẫu nhiên theo khối
Đối với phương pháp phân tích phương sai ở trên đánh giá sự khác nhau giữa trung bình của
tổng thể được thực hiện dưới hình thức ngẫu nhiên hoàn toàn, vì các giá trịquan sát của mẫu
hoàn toàn được chọn một cách ngẫu nhiên độc lập từtổng thể.
Giảsửta có mẫu các giá trịquan sát với nhóm (xét theo yếu tốnghiên cứu) và khối (xét
theo khối).
Khi đó ta có tất cả. = ô giá trịquan sát; vì mỗi ô chỉcó 1 giá trịquan sát nên ta sẽcó giá
trịquan sát.
Gọi là giá trịquan sát ứng với nhóm , khối .
Bảng giá trịquan sát trong phân tích ANOVA với nhóm và khối.
Khối
Nhóm
1
2
…
1
2
…
…
…
….
….
….
….
…
Phân tích phương sai với nhóm, khối được thực hiện như sau:
Giảthuyết : trung bình của tổng thể(xét theo yếu tốnghiên cứu) thì bằng nhau, nghĩa là
: = = = .
(Ta cũng có thể kiểm định giảthuyết : trung bình của tổng thể(xét theo khối) thì bằng
nhau, nghĩa là: = = = .)
B1. Tính các giá trịtrung bình nhóm (xét theo cột); (xét theo dòng); (xét theo cảdòng và
cột).
=∑; =∑; =∑=∑
5
B2. Tính các đại lượng
thểhiện sựbiến thiên do khác biệt giữa các nhóm xét theo yếu tốnghiên cứu
=(− )
thểhiện sựbiến thiên do khác biệt giữa các khối
= −
thểhiện sựbiến thiên do các yếu tốkhác không nghiên cứu, không thểgiải thích bởi các
nhóm hay các khối
= − − +
Khi đó ta có = + + . Đây chính là cơ sở phân tích phương sai hai yếu tố(khối
được xem như là yếu tốthứ hai, nhưng với giả định là không có sự tương tác giữa các nhóm và
khối, nghĩa là sựkhác nhau giữa các nhóm được giả định không đổiởtất cảcác khối).
B3. Tính các đại lượng trung bình
=−1; = −1; =(−1)( −1)
B4. Tính các giá trịkiểm định =và =.
Quy tắc quyết định: Bác bỏ: = = = ởmức ý nghĩa nếu
>,( )( ),; trong đó ,( )( ),có phân phối Fisher với( −1)bậc tựdo của
tửsốvà (−1)( −1)bậc tựdo của mẫu số.
(Bác bỏ: = = = ởmức ý nghĩa nếu>,( )( ),; trong đó
,( )( ),có phân phối Fisher với( −1)bậc tựdo của tửsốvà (−1)( −1)bậc
tựdo của mẫu số).