Nguyễn Hồng Nam, 2007
6
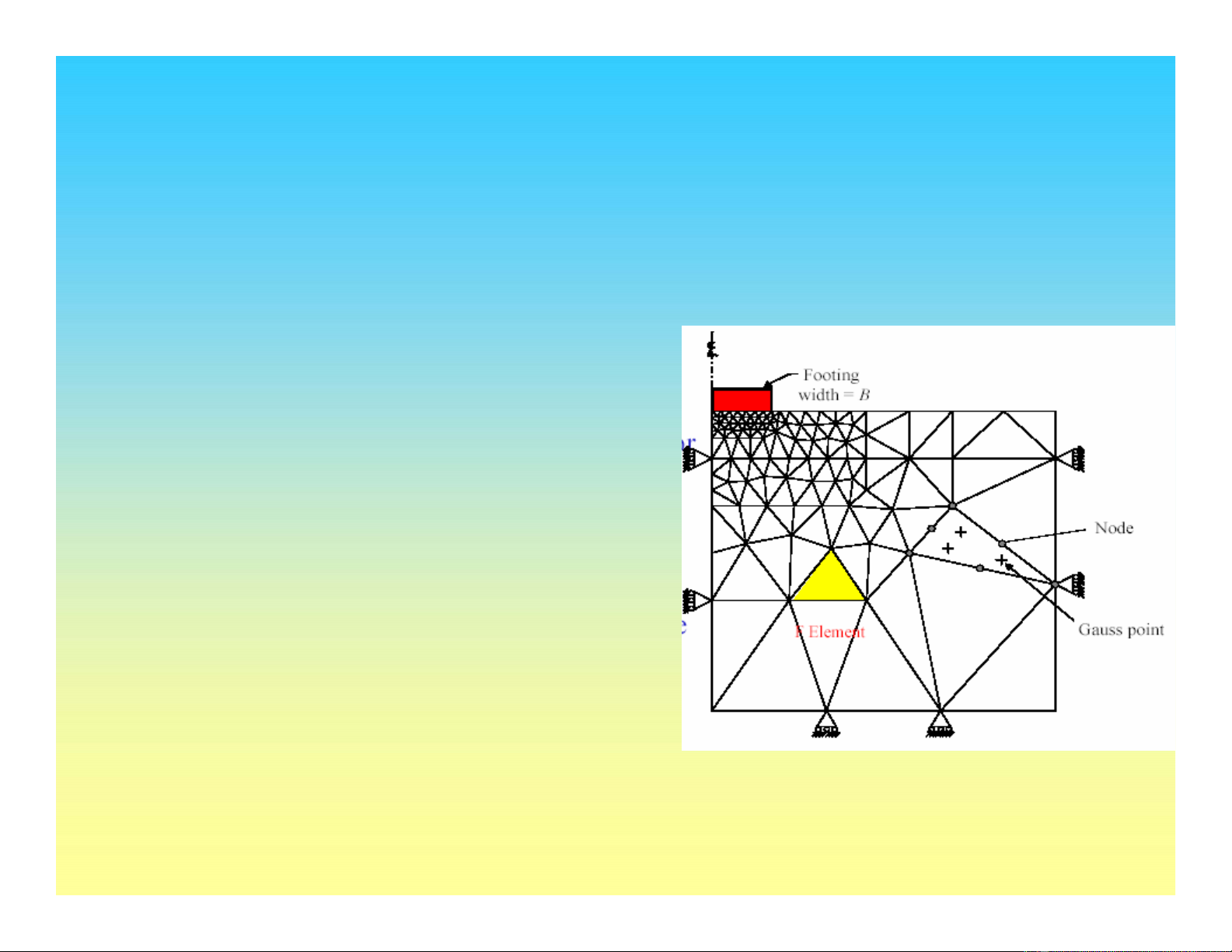
Các bước cơ bản của phương pháp PTHH
• Chia lưới phần tửhữu hạn
• Chuyển vịtại các nút là các ẩn số
• Chuyển vịbên trong phần tử được
nội suy từcác giá trịchuyển vịnút
• Mô hình vật liệu (quan hệứng suất-
biến dạng)
•Điều kiện biên vềchuyển vị, lực
•Giải hệ phương trình tổng thểcân
bằng lực cho kết quảchuyển vịnút
• Tính các đại lượng khác (biến dạng,
ứng suất).
Nguyễn Hồng Nam, 2007
7
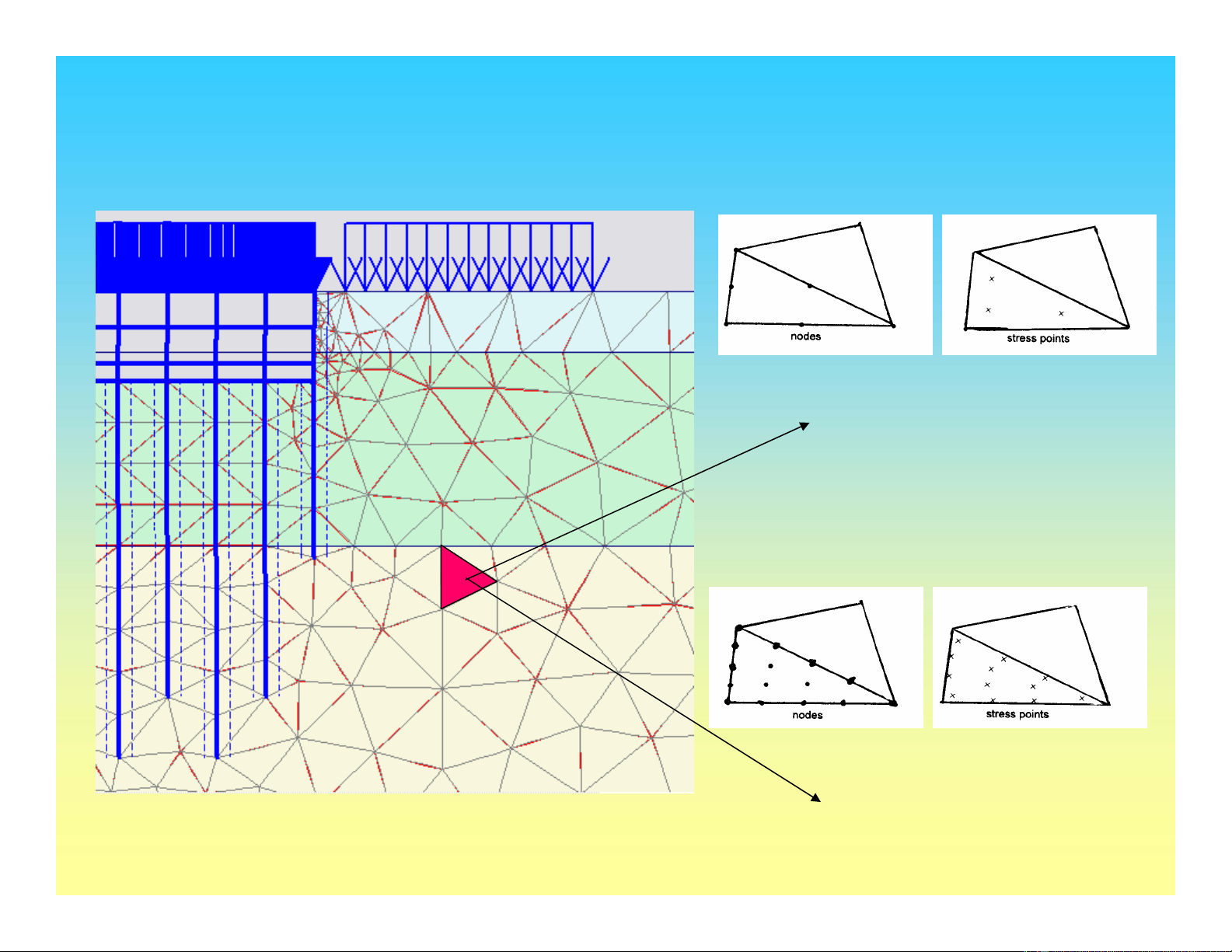
Các phần tử cơ bản
Phần tử 6 điểm nút
Phần tử 15 điểm nút
Lưới phần tửhữu hạn
Nguyễn Hồng Nam, 2007
8
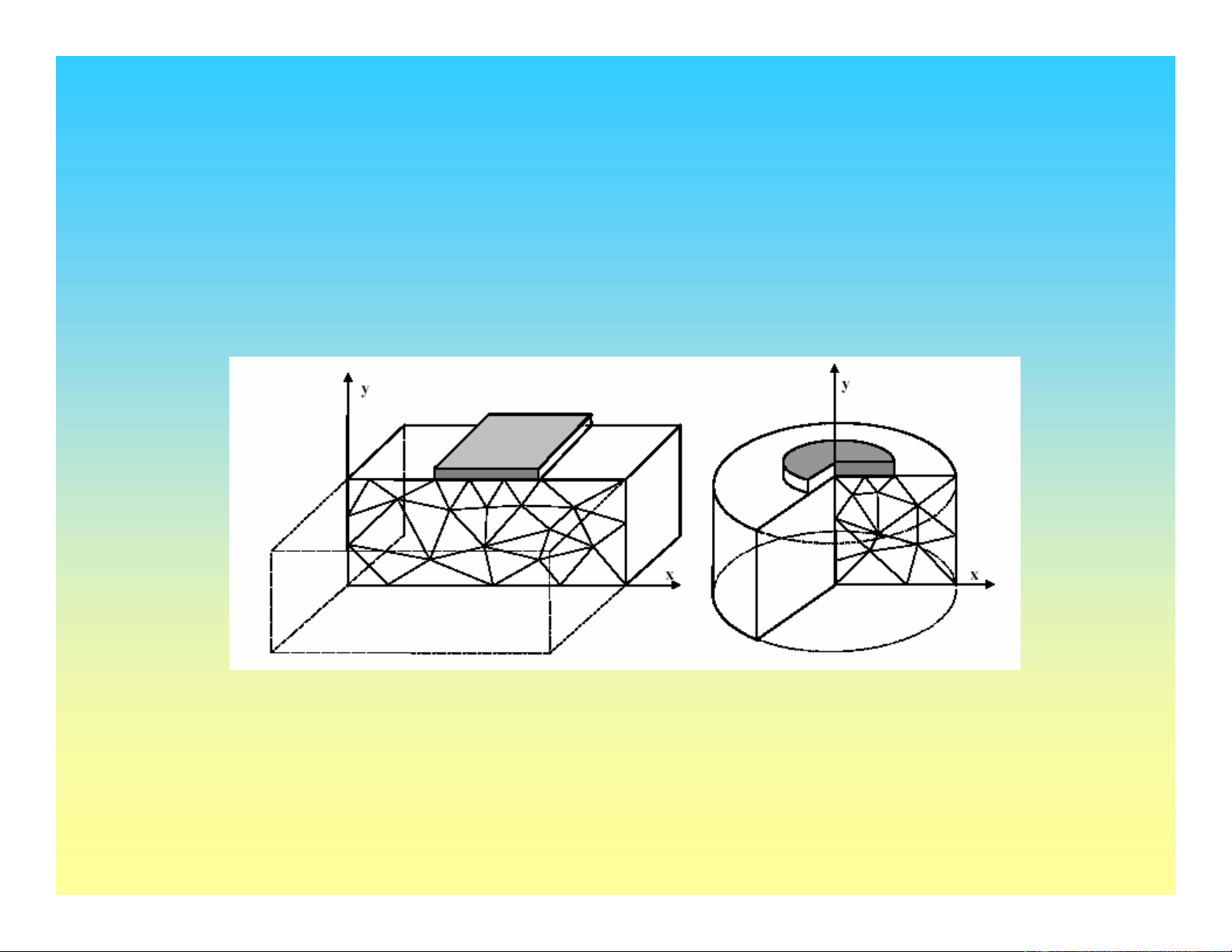
Mô hình bài toán
Biến dạng phẳng
(Plane strain)
Đối xứng trục
(Axis-symmetry)
Nguyễn Hồng Nam, 2007
9
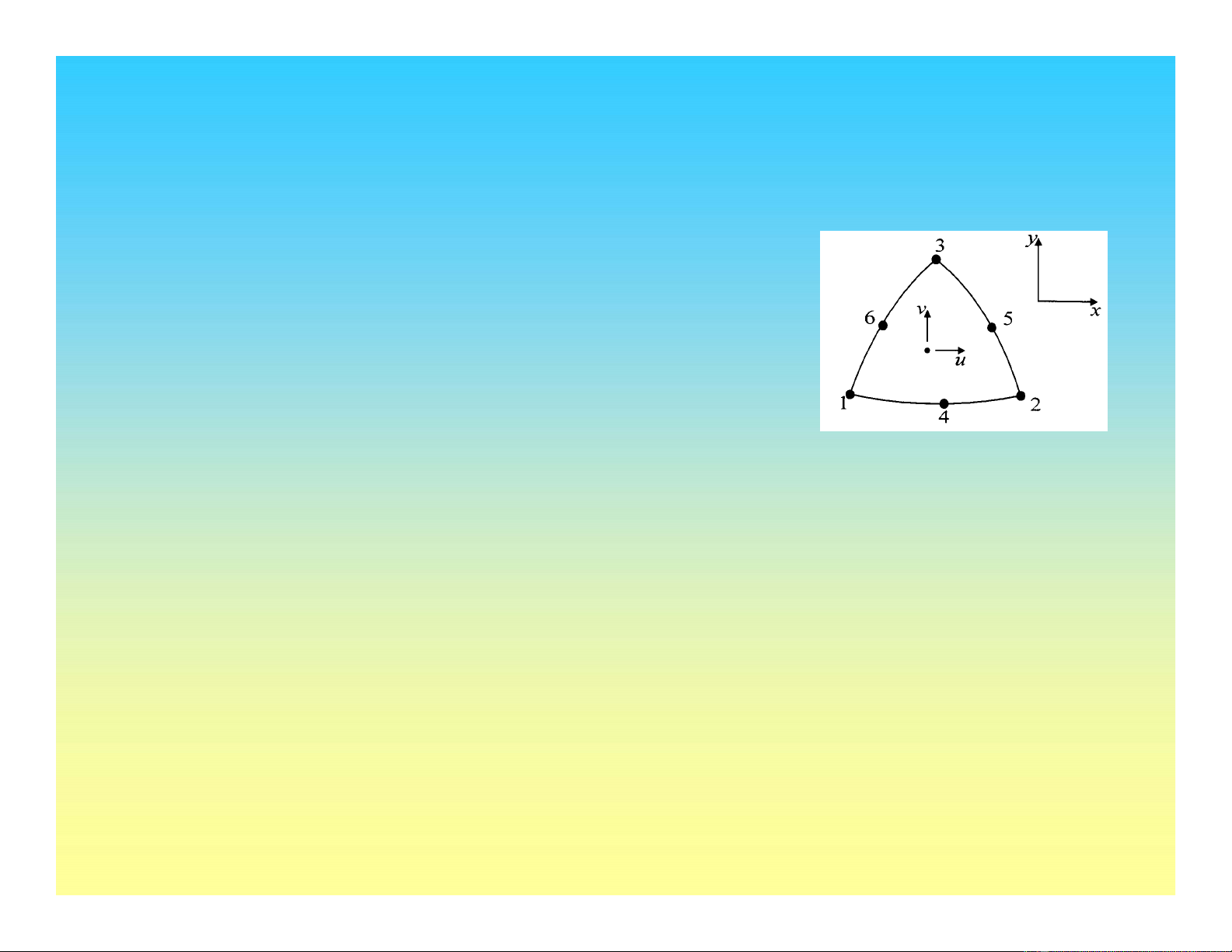
PhÇn tö 6 nót
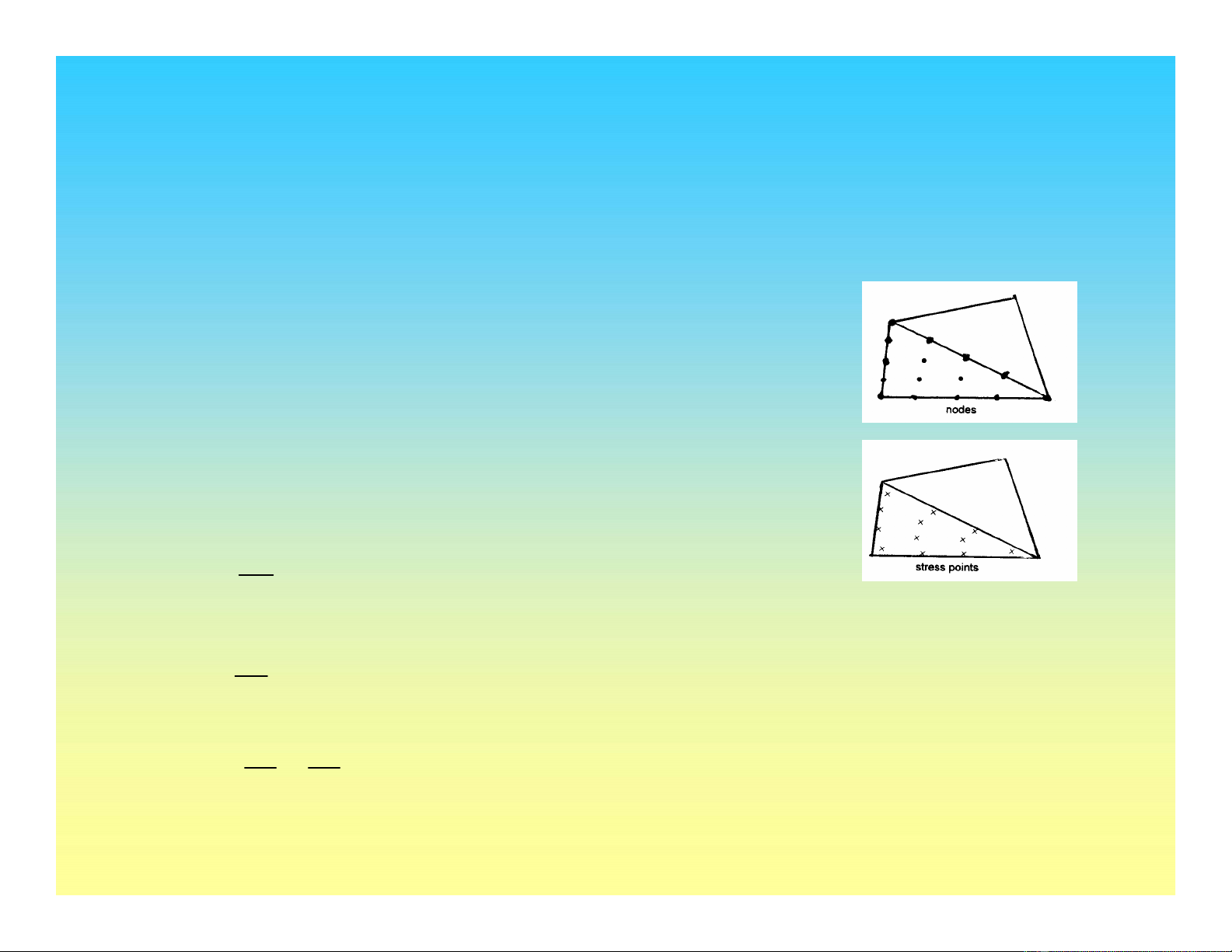
Phần tử 6 điểm nút: Nội suy bậc 2
u(x,y) = a0 + a1x + a2y + a3x2 + a4xy + a5y2
v(x,y) = b0 + b1x + b2y + b3x2 + b4xy + b5y2
Cách viết khác:
u = N1u1+N2u2+N3u3+N4u4+N5u5+N6u6=[N]{U}
v = N1v1+N2v2+N3v3+N4v4+N5v5+N6v6=[N]{V}
[N]: hàm dạng
Chuyển vị
Nguyễn Hồng Nam, 2007
10
Các phần tửbậc cao 15 nút: Sửdụng các đa thức bậc 4
Biến dạng: Tính từcác chuyển vị.
Đối với phần tử 6 điểm nút:
ε
δ
δ
xx
u
xaaxay
==+ +
134
2
ε
δ
δ
yy
v
xbbx by
==+ +
2
425
γ
δ
δ
δ
δ
xy
u
y
v
xbaa bx a by
=+=+ + + +
()( )( )
124 3 54
22
Biến dạng
u(x,y) = a0 + a1x + …………...+ a15y4
v(x,y) = b0 + b1x + …………...+ b15y4