
CHƯƠNG 5: BÀI TOÁN PHẲNG
08/01/2024 22:05 163
Nội dung:
5.0. Khái Niệm Bài Toán Phẳng
5.1. Bài Toán Phẳng Với Phần Tử Tam Giác (CST Element)
5.2. Bài Toán Phẳng Với Phần Tử Chữ Nhật
5.0. KHÁI NIỆM BÀI TOÁN PHẲNG (1/3)
Với bài toán không gian, việc giải hệ các phương trình là rất phức tạp, và dường
như không thực hiện được trong trường hợp tổng quát do các khó khăn về mặt
toán học.
Tuy nhiên, thực tế có nhiều bài toán có thể giải được nếu bổ sung một số giả
thiết đơn giản hóa, trong số đó có thể kể đến các BÀI TOÁN PHẲNG.
Hai dạng bài toán BÀI TOÁN PHẲNG:
ỨNG SUẤT PHẲNG BIẾN DẠNG PHẲNG
164
2
2
2
0
0
0
GGuX
x
GGvY
y
GGwZ
z
;
;
22
22
11
2
22
22
11
2
2
21
2
11
2
11 1
11
2
11 1
1
11
xxy
yyz
z
II
X
YZ X XY
x
yz x xy yx
x
II
X
YZ Y YZ
x
yz y yz zy
y
IXY
xy
z
;
2
21
1
21
zx
I
Z
ZZX
z
zzxxz
Phương trình Lamé Phương trình Beltrami - Michell
CHƯƠNG 5: BÀI TOÁN PHẲNG
5.0. KHÁI NIỆM BÀI TOÁN PHẲNG (2/3)
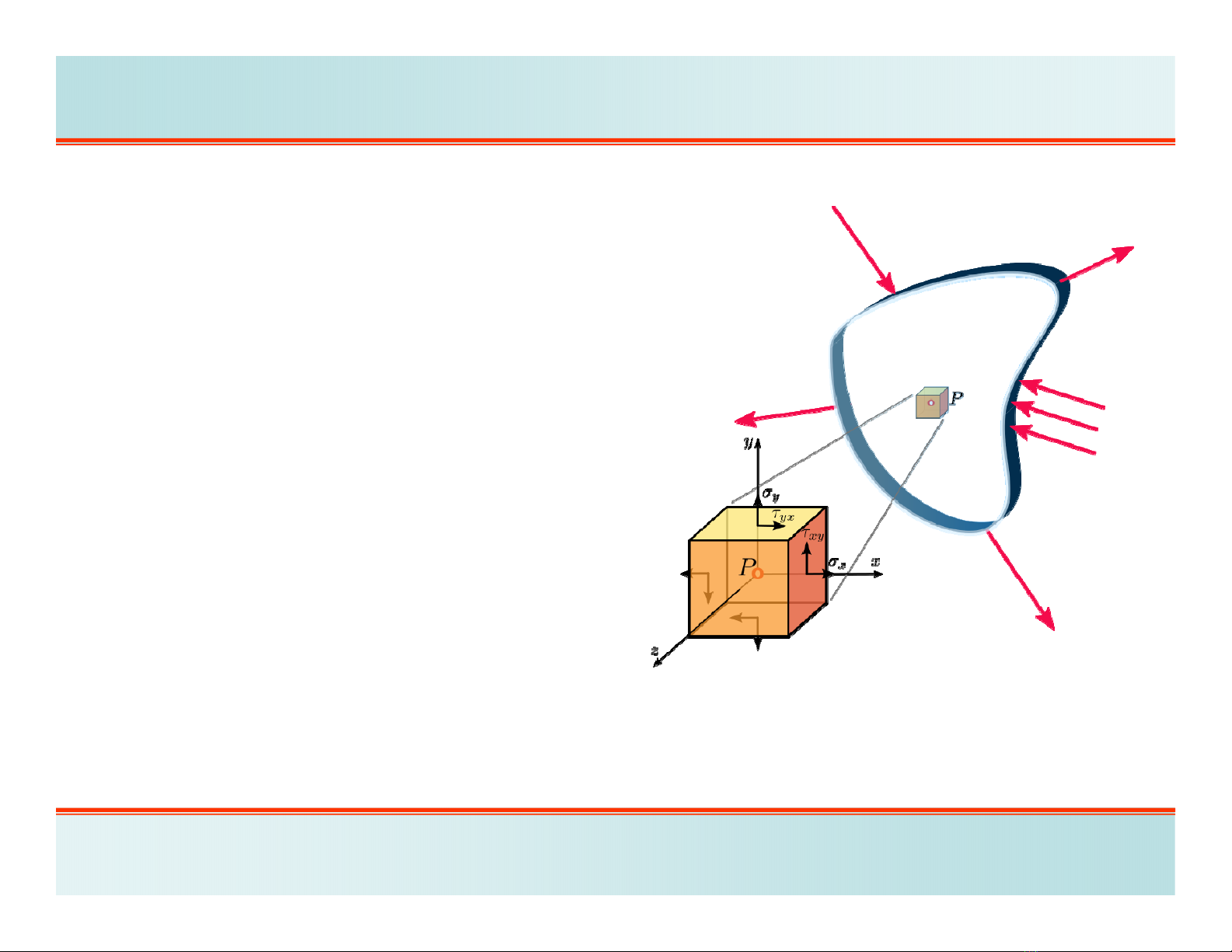
Khi vật thể có dạng tấm mỏng,
tải trọng nằm trong mặt phẳng
giữa tấm, phân bố đều theo bề dày
tấm thì có thể xem rằng:
a. Các ứng suất
z=
zx =
zy =0
b. Các ứng suất trong mặt phẳng
không đổi theo bề dày tấm,
không phụ thuộc tọa độ z
1. ỨNG SUẤT PHẲNG
165
H.5.1. Bài toán ứng suất phẳng
CHƯƠNG 5: BÀI TOÁN PHẲNG
5.0. KHÁI NIỆM BÀI TOÁN PHẲNG (3/3)
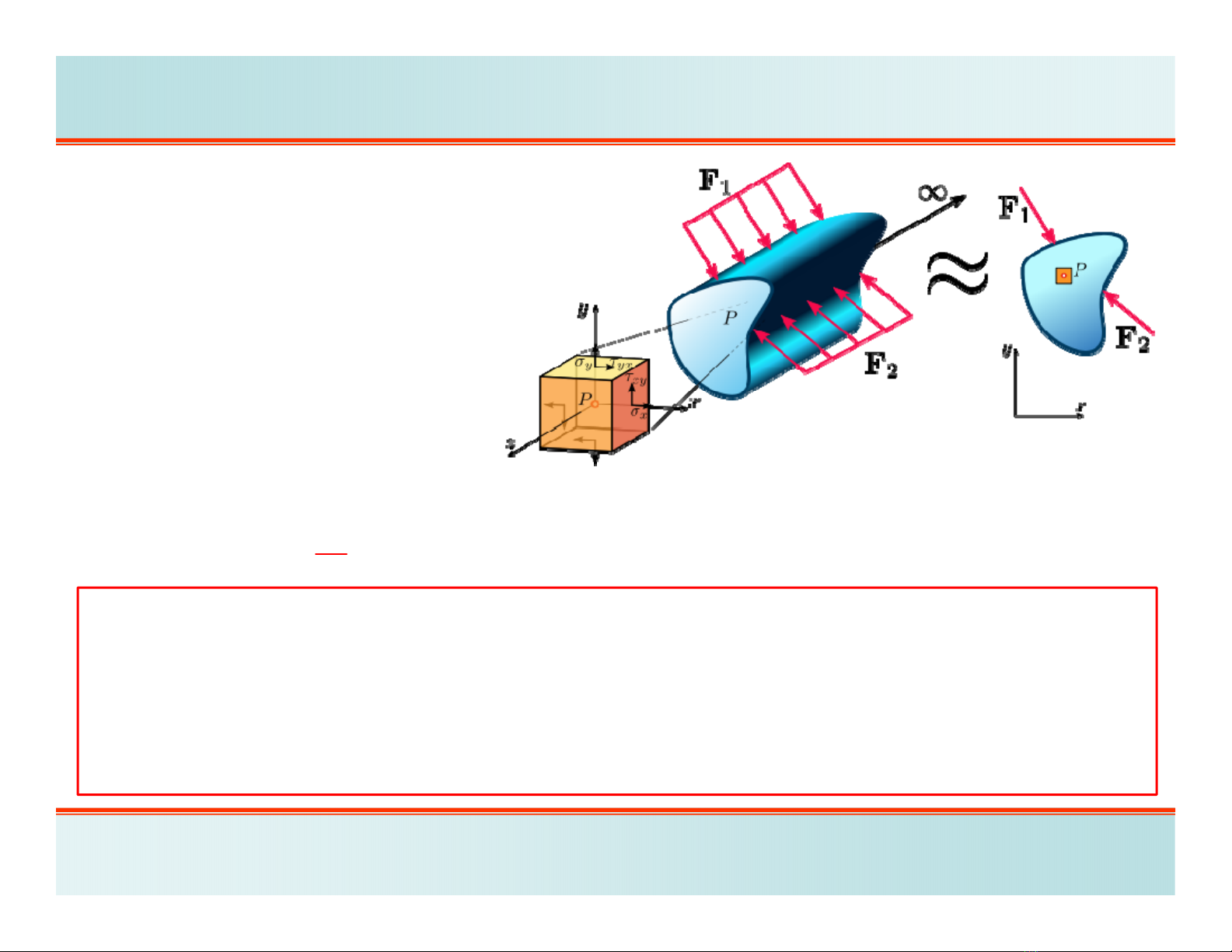
Khi bài toán có dạng lăng
trụ dài và có mặt cắt ngang
không đổi, chịu tải trọng
vuông góc với trục zvà phân
bố đều dọc theo chiều dài thì
ta có thể xem rằng w=0và
do đó suy ra:
2. BIẾN DẠNG PHẲNG
0;
z
w
z
0
zx zy
166
H.5.2. Bài toán biến dạng phẳng
Khigiảicácbài toán phẳng, chỉ cần quan tâm tới các phương trình cân bằng và
biến dạng trong mặt phẳng xOy, các phương trình này giống nhau cho cả bài toán
ứng suất phẳng và biến dạng phẳng.Chỉcóphương trình ứng xử của vật liệu là
khác nhau.
CHƯƠNG 5: BÀI TOÁN PHẲNG

5.1. Bài Toán Phẳng với Phần Tử Tam Giác (CST element)
167
Nội dung:
5.1.1. Hàm Dạng
5.1.2. Biến Dạng và Ứng Suất
5.1.3. Ma Trận Cứng Phần Tử
5.1.4. Vector Tải Trọng Nút Phần Tử
5.1.5. Ví Dụ - Bài Tập
CHƯƠNG 5: BÀI TOÁN PHẲNG











![Bài tập Vật lý sóng: Tổng hợp bài tập 6 [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250805/oursky04/135x160/401768817575.jpg)














