CHƯƠNG 3: TÍNH TOÁN HỆ THANH DÀN PHẲNG
08/01/2024 22:05 99
Nội dung:
3.1. Ma Trận Cứng Phần Tử
3.1.1. Trong Hệ Tọa Độ Địa Phương
3.1.2. Trong Hệ Tọa Độ Tổng Thể
3.2. Ma Trận Độ Cứng Tổng Thể
3.3. Áp Đặt Điều Kiện Biên Chuyển Vị
3.4. Bài Tập
3.5. Dàn không gian Sinh viên tự đọc thêm
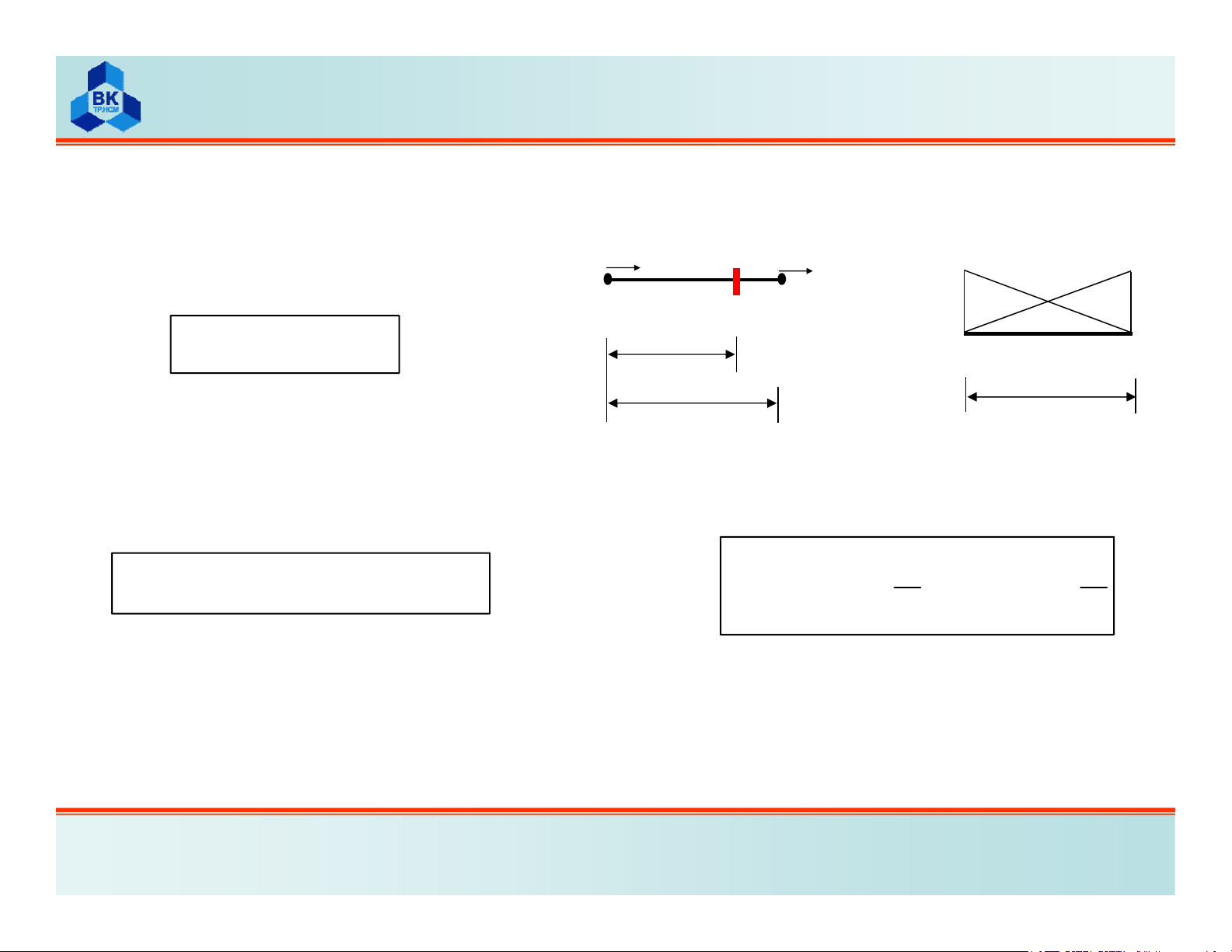
Biểu diễn chuyển vị Ktheo
các chuyển vị nút và các
hàm bậc nhất :
3.1. MA TRẬN CỨNG PHẦN TỬ (1/7)
3.1.1 – Trong hệtọađộ địaphương
ij
x
L
K
ui, Piuj, Pj
11
N1(x) N2(x)
L
ij
a) Chuyển vị và lực nút b) Các hàm dạng
Giả thiết chuyển vị tại Klà
hàm bậc nhất theo tọa độ vị
trí: 12
()ux a ax
ji uu ,
)(),( 21 xNxN
12
() () ()
ij
ux uN x uN x trong đó: 12
() 1 ; ()
x
x
Nx Nx
LL

Cáchàmnàyđượcgọilàhàm dạng (shape functions) hoặc hàm nội
suy (interpolation functions), có tác dụng xấp xỉ trường chuyển vị
trong phần tử theo các chuyển vị nút (ở 2 đầu i,jcủa phần tử).
100
(1)
(2)
Tính chất hàm dạng
CHƯƠNG 3: TÍNH TOÁN HỆ THANH DÀN
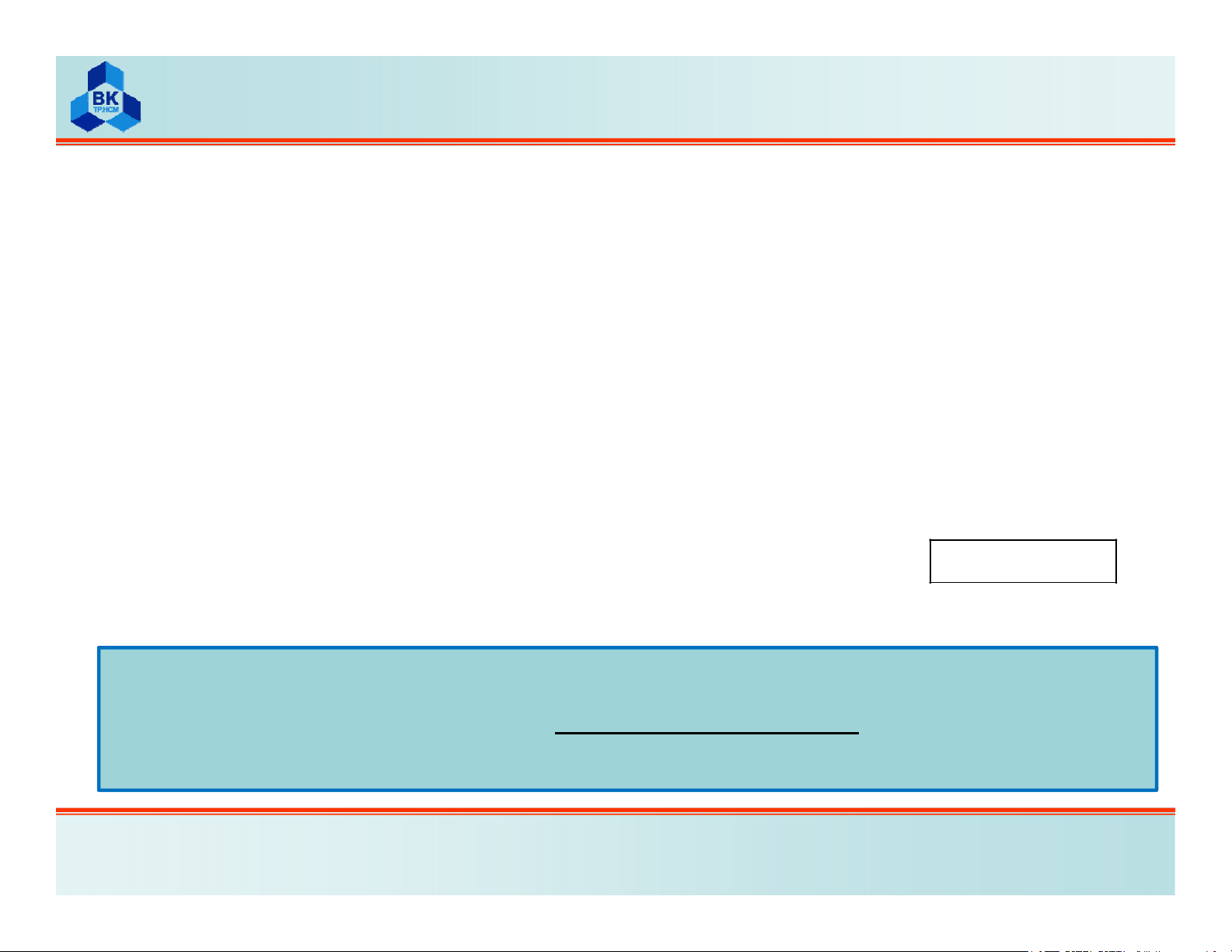
Nếu thế x=0 và x=L vào phương trình (1) và (2), ta thu được:
11
12 2
10
1
i
j
uaa
uaaL La




 

 


Phương trình có thể viết lại: 1
{}
[]
{} {}
[]
{}
ee e e
uAaha
y
aAu

trong đó: 1
10 1 0
[] []
11/1/
AA
L
LL




Phương trình (2) viết như sau: 12
() [ () ()] () [ ]
{}
i
e
j
u
ux N x N x ux N u
u






với: là ma trận các hàm dạng
12
[][ () ()]NNxNx
Như vậy, trường chuyển vị trong một phần tử dù chọn dưới dạng đa
thức, nhưng cuối cùng cũng biểu diễn được theo các hàm dạng và
các chuyển vị nút.
101
3.1. MA TRẬN CỨNG PHẦN TỬ (2/7) - tọađộ địaphương
(Mốiquanhệgiữa chuyểnvịnút và hệsốđathứcxấpxỉvà ngượclại)
(Thựchiện đồng nhất (1) và (2))
CHƯƠNG 3: TÍNH TOÁN HỆ THANH DÀN
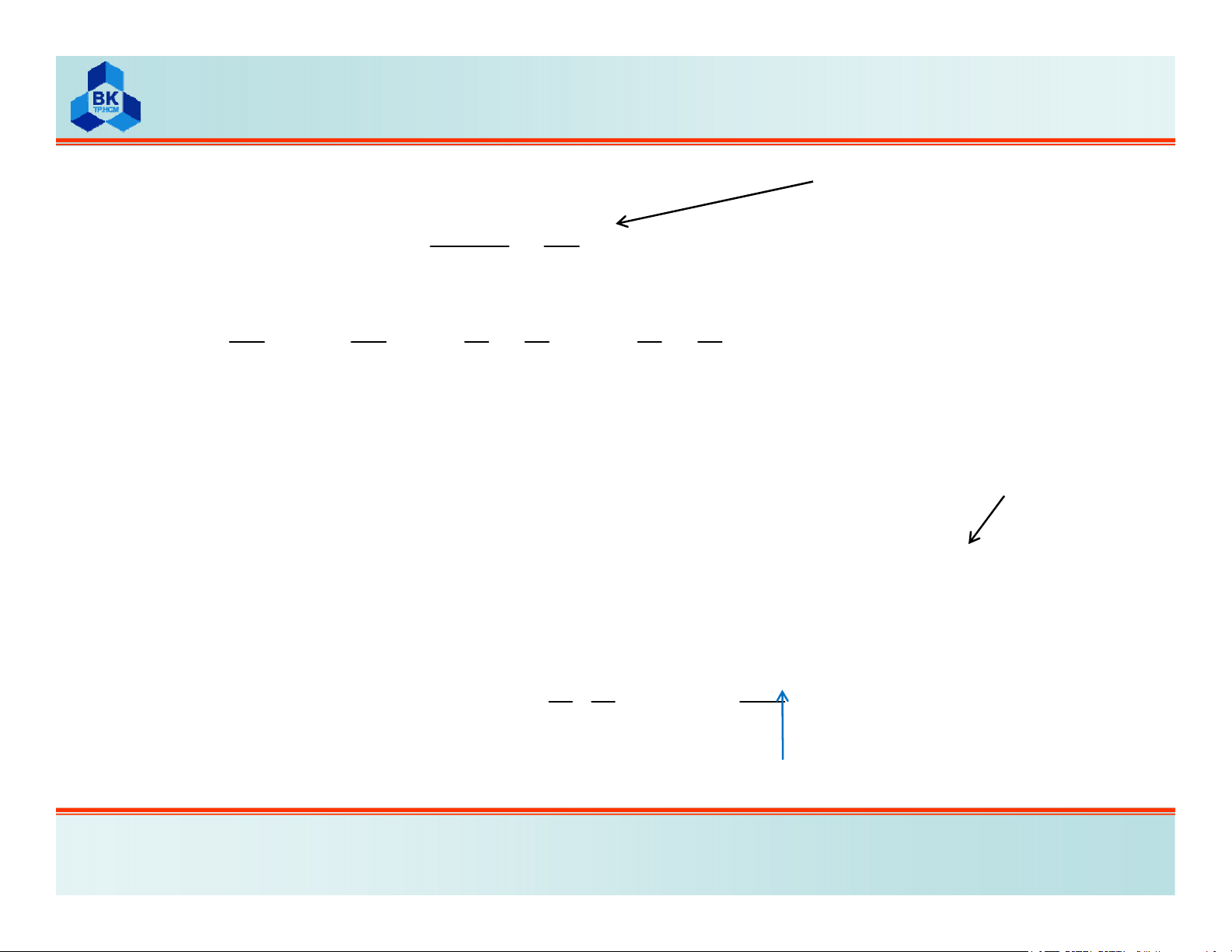
Khi này biến dạng được tính theo Cauchy:
() [ ]{} [ ]{}
ee
ux Nu Bu
xx


với 11
[] [ ] 1 xx
BN
x x LL LL






gọi là ma trận
tính biến dạng.
Ứng suất, lực dọc trong thanh: []{}
[]{}
e
e
EEBu
NF EFBu

Từ điều kiện cân bằng nút, ta có: 1
1
ii
jj
PN P N
PN P








Vậy ta có: 111
11
111

 



 




 
iii
j
jj
Puu
EA
EA
Puu
LL L
102
3.1. MA TRẬN CỨNG PHẦN TỬ (3/7) - tọađộ địaphương
Ma trận hàm dạng
Lực dọc
trong thanh
CHƯƠNG 3: TÍNH TOÁN HỆ THANH DÀN
Ghi chú: F (ký hiệutrướcđây) ≡A (ký hiệumới)
là diện tích mặtcắt ngang
hay viết gọn lại ta có:
e
ee
P
Ku
với vector lực nút của phần tử e
vector chuyển vị nút của phần tử e

e
P

e
u


11
11
e
e
e
AE
KL
ma trậnđộ cứng phầntử
kéo nén đúng tâm trong hệ
tọađộ địaphương
103
3.1. MA TRẬN CỨNG PHẦN TỬ (4/7) - tọađộ địaphương
CHƯƠNG 3: TÍNH TOÁN HỆ THANH DÀN
Trong đó:
•Alà diện tích mặt cắt ngang của phần tử
•Elà mô đun đàn hồi vật liệu phần tử
•Llà chiều dài phần tử