2/23/2020
1
VŨ NGỌC SƠN
BỘ MÔN CƠ HỌC KẾT CẤU
TRƯỜNG ĐẠI HỌC XÂY DỰNG
0983 880 553
Email: sonvn@nuce.edu.vn
PHƯƠNG PHÁP
PHẦN TỬ HỮU HẠN
GIỚI THIỆU CHUNG
GIỚI THIỆU CHUNG
The contents in this note are copied and reproduced from various publications for education only
FEM – FINITE ELEMENT METHOD
GIỚI THIỆU CHUNG
The contents in this note are copied and reproduced from various publications for education only
FEM – FINITE ELEMENT METHOD
1 2
3 4
2/23/2020
2
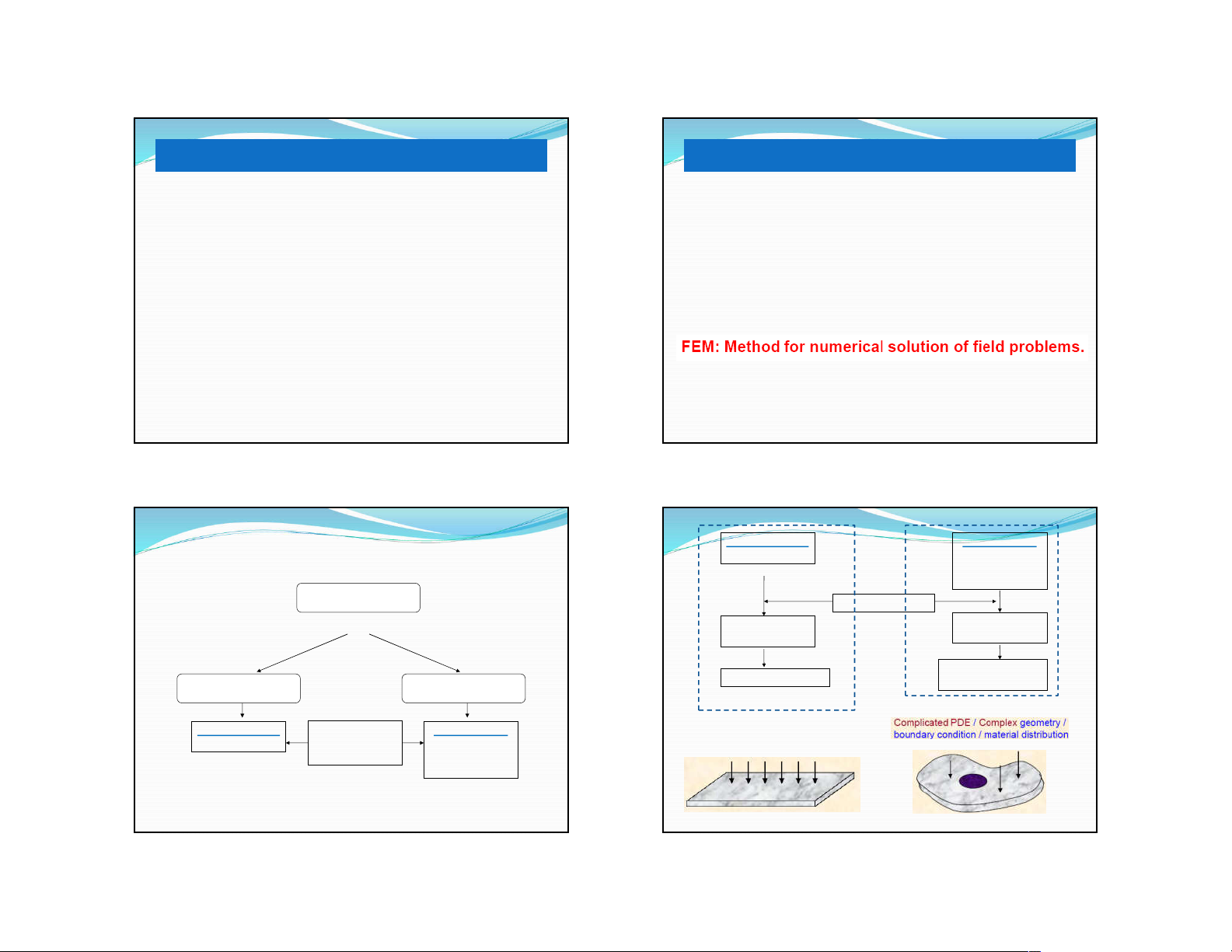
GIỚI THIỆU CHUNG – bài toán trường
Khi giải quyết các vấn đề (bài toán) trong kỹ thuật ta
thường phải xác định sự phân bố của đại lượng nghiên
cứu (biến số) trên toàn bộ miền đang xét. Biến số này
phải thỏa mãn một phương trình vi phân nào đó (the
governing differential equation) trên toàn bộ miền đang
xét và thỏa mãn các điều kiện biên xác định(boundary
conditions).
Bài toán như vậy được gọi là bài toán giá trị biên
(boundary value problems) hay là bài toán trường (field
problems) trong kỹ thuật. e.x phân tích kết cấu và vật rắn
biến dạng; phân tích truyền nhiệt hoặc điện, phân tích
dòng chảy chất lỏng…
The contents in this note are copied and reproduced from various publications for education only
GIỚI THIỆU CHUNG – bài toán trường
Biến số (or biến trường) thường là chuyển vị hoặc ứng
suất; nhiệt độ hoặc thông lượng nhiệt ….
Điều kiện biên là các giá trị xác định của biến số (hoặc
các đại lượng liên quan của biến số như là đạo hàm...)
trên biên của miền đang xét .
Miền đang xét là các vật thể thực được nghiên cứu.
The contents in this note are copied and reproduced from various publications for education only
The contents in this note are copied and reproduced from various publications for education only
7
Giải các bài toán kỹ thuật
(Solving Engineering Problems)
BÀI TOÁN KỸ THUẬT
Lựa chọn phương pháp giải
PP GIẢI TÍCH PP SỐ
Các giả thiết,
Các xấp xỉ,
Đơn giản hóa
Mô hình liên tục
mô hình toán
Mô hình rời rạc
mô hình toán được
biểu diễn bằng các
hàm đơn giản
(see following slides)
The contents in this note are copied and reproduced from various publications for education only
8
Mô hình liên tục
mô hình toán
Mô hình rời rạc
mô hình toán được
biểu diễn bằng các
hàm đơn giản
Giải bằng pp giải
tích toán học
Nghiệm giải tích
"Typically, only possible for regular
/ simple geometries and boundary
conditions"
Giải bằng pp số
toán học
Nghiệm gần đúng
dạng số
Điều kiện biên
5 6
7 8
2/23/2020
3
GIỚI THIỆU CHUNG – Các pp số
The contents in this note are copied and reproduced from various publications for education only
* FEM ~ Finite Element Method
** FEA ~ Finite Element Analysis
Các phương pháp số
• Sai phân hữu hạn (Finite Difference Method)
• Dải hữu hạn (Finite Strip Method)
•Phần tử hữu hạn (FEM or FEA)
• Phần tử biên (Boundary Element Method)
• Phương pháp không lưới (Meshless Method)
• …
Phương pháp Phần tử hữu hạn mô hình chuyển vị
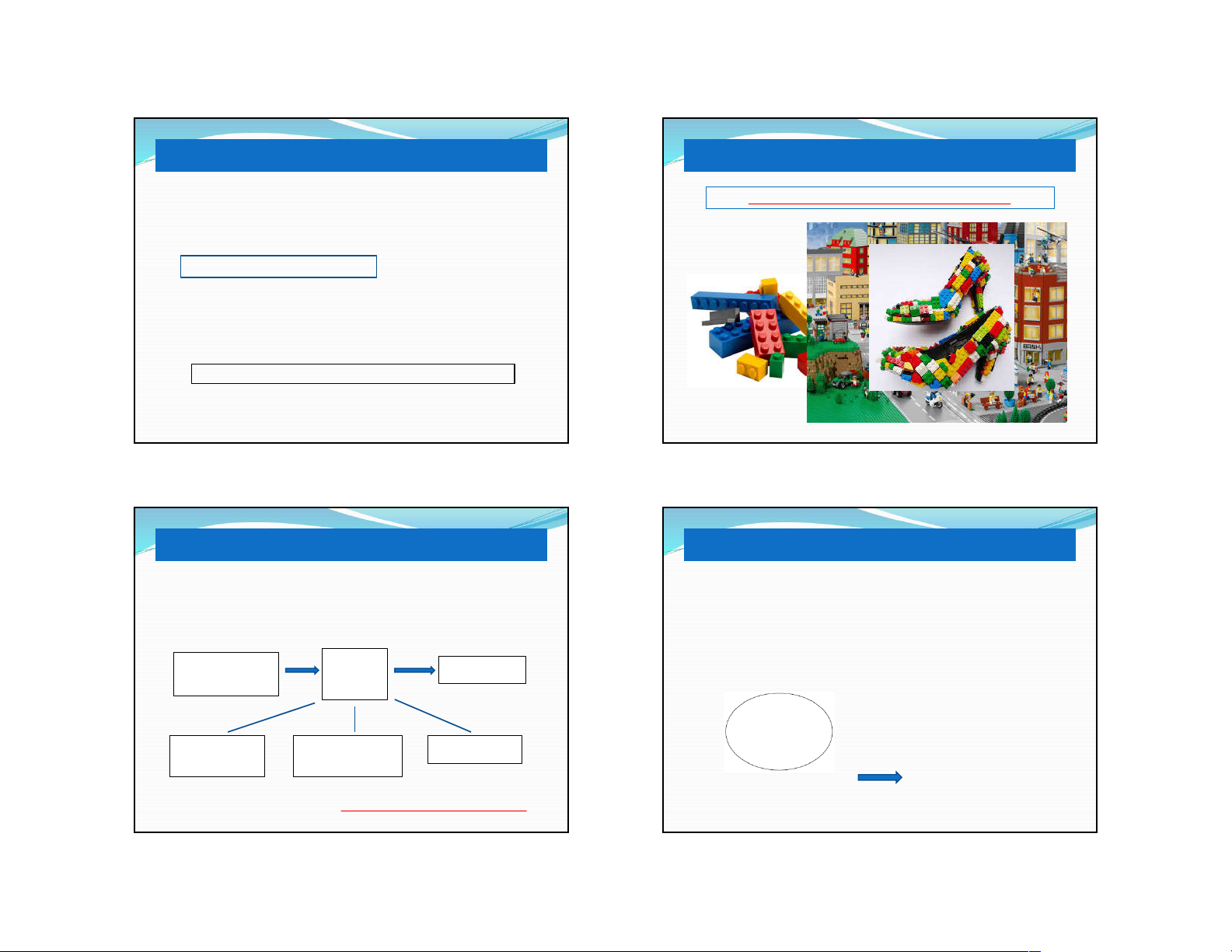
PP PTHH – NGUYÊN TẮC CƠ BẢN
Xếp hình Lego
The contents in this note are copied and reproduced from various publications for education only
“Phức tạp” ≈ sự kết hợp các “đơn giản”
PP PTHH – NGUYÊN TẮC TÍNH TOÁN
PP PTHH (FEM* or FEA**) là một phương pháp tính (toán
học) dùng để tìm nghiệm xấp xỉ dạng số cho các bài toán
giá trị biên (bài toán trường) trong kỹ thuật.
The contents in this note are copied and reproduced from various publications for education only
* FEM ~ Finite Element Method
** FEA ~ Finite Element Analysis
BÀI TOÁN TRƯỜNG
(dạng pt vi phân
riêng phần)
NGHIỆM XẤP XỈ
DẠNG SỐ
Rời rạc hóa thành
hữu hạn các miền
nhỏ hơn (phần tử
)
Tìm nghiệm gần
đúng cho riêng từng
phần tử
Ghép nối tất cả
các phần tử lại
PP
PTHH
FEM is a mathematical tool
PP PTHH – NGUYÊN TẮC TÍNH TOÁN
Bài toán trường:
Xét miền xác định V (hình 1.a)
Tính chất vật lý, điều kiện biên, phương trình vi phân đã biết
Xác định giá trị đại lượng nghiên cứu φ tại mọi điểm P(x,y)
trong miền V (i.e. vô hạn bậc tự do)
φ(x,y) = ???
Nghiệm giải tích = NOT OK
The contents in this note are copied and reproduced from various publications for education only
Hình 1.a: Miền xác định V
Nghiệm số xấp xỉ
FEM
•P(x, y)
9 10
11 12
2/23/2020
4
PP PTHH – NGUYÊN TẮC TÍNH TOÁN
Bài toán trường:
Phần tử tam giác dx
x
dy (hình 1.b) ≠ phân tố (i.e. hữu hạn bậc tự do)
Đỉnh tam giác được đánh số gọi là nút; Giá trị của biến số tại các nút
được gọi là bậc tự do (DOF). Số DOF của mỗi phần tử = số nút nhân
với số giá trị biến số cần xác định tại mỗi nút.
Các phần tử được nối với nhau tại các nút (hình 1.c)
The contents in this note are copied and reproduced from various publications for education only
Hình 1.b: Phần tử trong
miền xác định V
Hình 1.c: Ghép nối các
phần tử trong miền V
Divide and conquer
PP PTHH – NGUYÊN TẮC TÍNH TOÁN
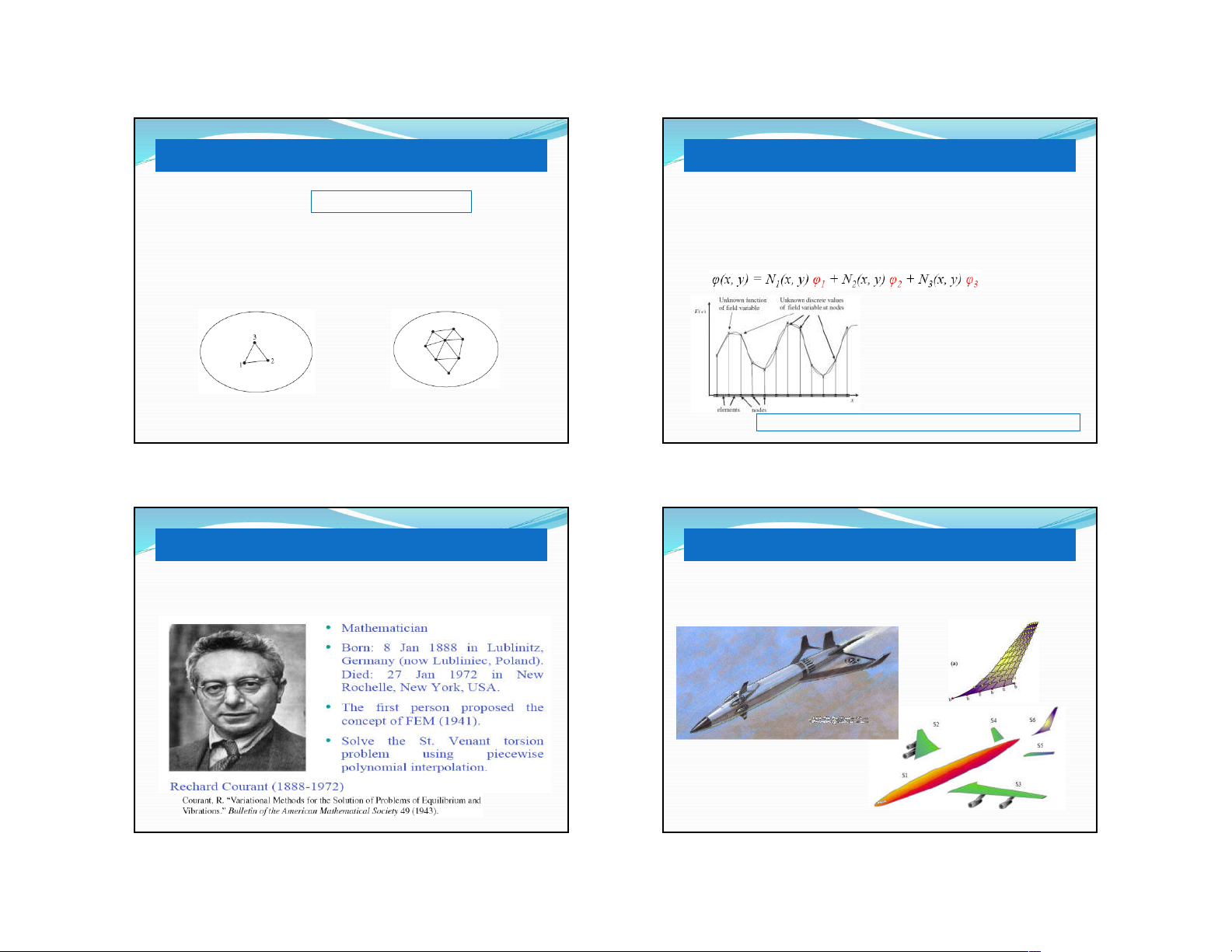
PP PTHH sẽ tính giá trị biến số tại các nút
Giá trị của biến số φ tại điểm bất kỳ bên trong mỗi phần tử sẽ
được nội suy theo các giá trị đã biết tại nút (bậc tự do)
M ~ số bậc tự do của phần tử
N
i
~ hàm nội suy (hàm dạng) mô
tả sự biến thiên của biến số φ trên mỗi
phần tử. Hàm dạng phải được xác
định trước (thường chọn là hàm đa
thức) và là hàm số của các biến độc
lập (x, y, z).
( )
1
( , , ) ( , , ).
M
e
i
i
i
x y z N x y z
ϕ
Ở một mức độ nào đó, đường thẳng và đường cong là xấp xỉ
PP PTHH – Lịch sử phát triển
1943 --- Courant : phương pháp biến thiên (Variational
methods)
The contents in this note are copied and reproduced from various publications for education only
PP PTHH – Lịch sử phát triển
1956 --- Turner, Clough, Martin and Topp : phương pháp độ
cứng trực tiếp (Direct stiffness methods)
The contents in this note are copied and reproduced from various publications for education only
13 14
15 16
2/23/2020
5
PP PTHH – Lịch sử phát triển
1956 --- Turner, Clough, Martin and Topp : phương pháp độ
cứng trực tiếp (Direct stiffness methods)
1960 --- Clough lần đầu tiên sử dụng thuật ngữ “phần tử hữu
hạn” trong bài toán phân tích trạng thái ứng suất phẳng & bắt
đầu ứng dụng trong kết cấu xây dựng
1960s – 1970s --- PP PTHH được áp dụng rộng rãi trong các
nghành kỹ thuật
O. Zienkiewicz viết quyển sách đầu tiên về FEM
The contents in this note are copied and reproduced from various publications for education only
PP PTHH – Lịch sử phát triển
O. Zienkiewicz viết quyển sách đầu tiên về FEM
The contents in this note are copied and reproduced from various publications for education only
PP PTHH – Ưu điểm
Phương pháp tính linh hoạt (Versatility): có thể áp dụng linh
hoạt cho các bài toán trường trong các “miền” có hình dạng,
tính chất vật lý và cơ lý, điều kiện biên bất kỳ.
The contents in this note are copied and reproduced from various publications for education only
PP PTHH – Ưu điểm
Phương pháp tính linh hoạt (Versatility):
The contents in this note are copied and reproduced from various publications for education only
17 18
19 20