Quản trị rủi ro trong cơ sở sản xuất kinh doanh nông nghiệp: Kinh nghiệm và giải pháp (Phần 2)



Trưng ði hc Nông nghip Hà Ni - Giáo trình Qan tr ri

ro -------------------------------------------------



CHƯƠNG III-3

QUYT ðNH DƯI ðIU KIN RI RO

Mc ñích ca chương:

Hc xong chương này sinh viên s hiu:

- Mt s mô hình quyt ñnh khác nhau

- Cách xác ñnh giá tr kỳ vng

- Cách sp xp thông tin trong phân tích ri ro

- Các qui tc quyt ñnh dưi ñiu kin ri ro

Chương 2 chúng ta ñã ñ cp ñn các thái ñ khác nhau ca ngưi ra quyt ñnh ñi

vi ri ro và các phương pháp ñánh giá thái ñ ca h ñi vi ri ro. Trong chương này

chúng ta s bàn ñn ba mô hình quyt ñnh. Và như ñã nói  chương trưc, mc tiêu ca

ngưi ra quyt ñnh là tho mãn giá tr kỳ vng, vì vy chương này cũng s trình bày mt s

cách xác ñnh các giá tr kỳ vng da trên cơ s áp dng các qui tc quyt ñnh dưi ñiu

kin ri ro.

1. Các mô hình quyt ñnh

Trong phn này s ñ cp ñn các qui tc quyt ñnh gn vi 3 mô hình quyt ñnh:

(1) quyt ñnh không ñòi hi có thông tin xác sut, (2) an toàn ñt lên hàng ñu, (3) ti ña

hoá li ích kỳ vng

1.1. Quyt ñnh không ñòi hi thông tin xác sut

Halter và Dean (1971) ñã ñưa ra 4 qui tc quyt ñnh không ñòi hi thông tin v xác sut, ñó

là:

- Qui tc kt qu tt nht trong các kt qu xu nht (Maximin)

- Qui tc kt qu tôt nht trong các kt qu tt nht (Maximax)

- H s α ca Hurwicz

- Nguyên tc lý do không ñy ñ (nguyên tc LaPlace)

a) Qui tc Maximin

Qui tc này hưng vào chn kt qu xu nht ca mi chin lưc và b qua các kt

qu khác. Trong trưng hp này ngưi quyt ñnh cho rng kt qu xu s xy ra bt k anh

ta chn chin lưc nào, do ñó anh ta la chn kt qu tt nht trong các kt qu xu nht.

b) Qui tc Maximax

Nguyên tc này ngưc li vi nguyên tc trên vì ch chú ý ñn kt qu tt nht ca

mi chin lưc và b qua các kt qu khác. Qui tc này la chn giá tr cao nht trong các

giá tr tt nht .

c) Qui tăc h s α ca Hurwicz

Qui tc h s α - Hurwicz th hin như sau:

max [I

= α (M

) + (1- α)(m

)] (3.1.)

H s α do ngưi quyt ñnh ñưa ra vi ñiu kin 0 <α <1

là giá tr thu ñưc ln nht ca hot ñng j

là giá tr thu ñưc nh nht ca hot ñng j



Trưng ði hc Nông nghip Hà Ni - Giáo trình Qan tr ri

ro -------------------------------------------------



d) Nguyên tc LaPlace

Nguyên tc này có th s! dng khi không bit xác sut ca t"ng kt qu và do ñó

ngưi quyt ñnh coi như xác sut ca các kt qu là như nhau. Trong trưng hp này giá tr

ln nht s ñưc la chn, ñó là giá tr bình quân ñơn gin.

1.2. Mô hình quyt ñnh an toàn ñt lên hàng ñu

Như ñã tóm tt  chương 2, ñây là nguyên tc ngưi quyt ñnh trưc tiên mun tho mãn s

thích ca mình là an toàn trong kinh doanh sau ñó mi là mc tiêu li nhun, hay nói cách

khác là phi tho mãn ràng buc ri ro. Khái nim ri ro trong mô hình quyt ñnh này là

kh năng thit hi. Ràng buc ri ro trong mô hình an toàn ñt lên hàng ñu ñưc biu th

như sau:

P(∏ ≤ d) ≤ α (3.2)

Trong ñó ∏ là thu nhp ng%u nhiên ca mt hot ñng, d là ngư&ng thu nhp cn ñt ñưc

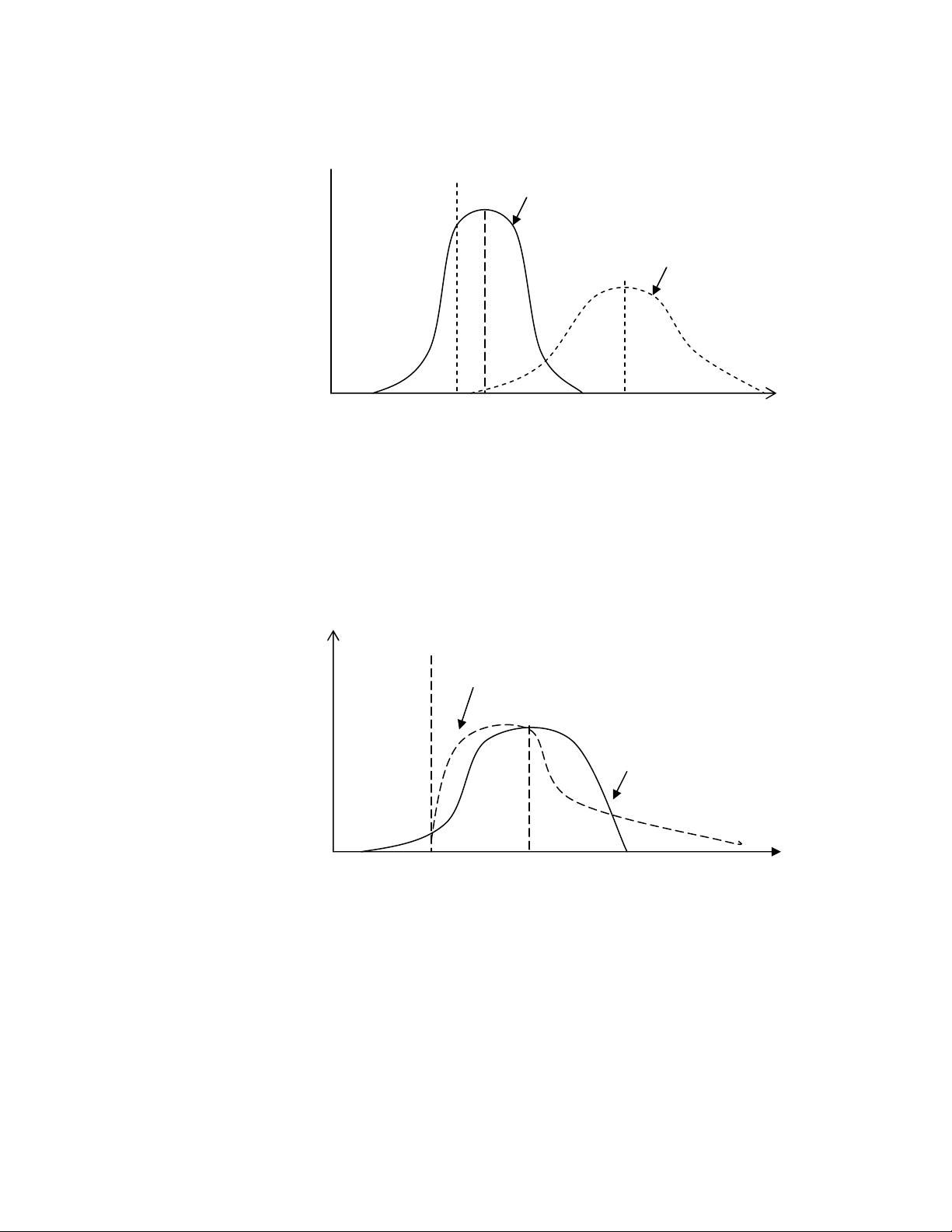
vi xác sut α . Các ñ' th 3.1a và 3.1b ch ra s trái ngưc nhau rt quan trng gi(a kh

năng thit hi và phương sai (variance) - là nh(ng thưc ño ri ro. Kh năng thit hi  phân

phi 1a cao hơn  2a và 1b cao hơn 2b vì α

> α

 c hai ñ' th. Ngưc li phương sai 

vùng 2a cao hơn  vùng 1a, còn  1b và 2b là như nhau vì σ

< σ

 ñ' th 3.1a và σ

 ñ' th 3.1b.



Trưng ði hc Nông nghip Hà Ni - Giáo trình Qan tr ri

ro -------------------------------------------------



1 >

< σ

(Xác sut)

∏= thu nhp thun

d = M*c thu nhp “tai ha”

; σ

; (Mi)i = trung bình; phương sai; ñ lch ca phân phi i

= Pi(∏ <d) ca phân phi i

1 >

12=

(Mi)

< …< (Mi)

(Xác sut)

ð' th 3.1: kh năng t,n tht và phương sai

1.3.Ti ña hoá li ích kỳ vng

Li ích kỳ vng ca mt hot ñng Aj ñưc th hin như sau:

(EU) = ∑ [ ∏(Si, Aj) P(Si)] (3.3)

j=1

Trong ñó EU là li ích kỳ vng, ∏ ( S

i , Aj

) là m*c thu nhp th* i ca ñc tính S

và hot

ñng A

U[∏(S

i , Aj

)] là li ích tương ñương ca m*c thu nhp ñó ; P(S

) là xác sut xy ra

















∏











Phân phi

ð

∏



Phân phi





Trưng ði hc Nông nghip Hà Ni - Giáo trình Qan tr ri

ro -------------------------------------------------



ca ñc tính th* i. Theo dãy s m rng ca Taylor , li ích kỳ vng ca hot ñng A

cũng

ñưc th hin như sau:

(EU) = f(µ

, σ

, M3j, M4

j ….

) (3.4.)

Trong ñó EU là li ích kỳ vng, µ

, σ

, M3j, M4

tương *ng là trung bình, phương sai, ñ

lch, kurtosis. Hoc ñơn gin hơn ta có hàm li ích:

(EU) = f(µ

, σ

) (3.5)

Trong ñó EU là li ích kỳ vng, µ

là trung bình, σ

là phương sai.

Và hot ñng có li ích kỳ vng ti ña (3.4) và (3.5) s ñưc la chn.

2. Quyt ñnh dưi ñiu kin ri ro

2.1. Kt qu kỳ vng và s bin ñ ng

S t'n ti ca ri ro làm cho quyt ñnh thêm ph*c tp và khó khăn hơn. Nhưng

quyt ñnh thì v%n phi làm và phi cân nhc ñn ri ro và ñiu không chc chn. Trong mt

môi trưng t'n ti ri ro thì các quyt ñnh thưng ñưc da trên các giá tr kỳ vng như

năng sut kỳ vng, chi phí kỳ vng và giá kỳ vng. Không có gì ñm bo các giá tr kỳ vng

s là kt qu thc ca quyt ñnh vì mi kt qu tim năng có mt xác sut riêng ca nó. Kt

qu ca quyt ñnh ch ñưc bit trong tương lai. ð ra quyt ñnh trong mt th gii ñy ri

ro, nhà quyt ñnh phi hiu cách th hin nh(ng kỳ vng như th nào, s! dng xác sut ra

sao và phân tích s bin ñng ca các kt qu tim năng th nào. Sau ñây là mt s cách th

hin kt qu kỳ vng

2.2. Phương pháp xác ñnh giá tr kỳ vng

Có nhiu phương pháp biu th gía tr kỳ vng v năng sut, v giá hoc các giá tr

khác khi không bit chúng mt cách chc chn. Khi có ñưc các giá tr kỳ vng thì ta có th

s! dng nó ñ lp k hoch và ra quyt ñnh vì ñó là các”ưc lưng tt nht” cho các giá tr

chưa bit và ch xác ñnh chính xác trong tương lai.

a) S trung bình

Có 2 loi con s trung bình có th s! dng ñ tính kỳ vng. Mt là s trung bình/bình

quân ñơn gin ñưc tính t" s liu qúa kh*, như s liu v năng suât hoc gía. ðây là

phương pháp ñơn gin thưng ñưc s! dng khi có s.n s liu thng kê. Vn ñ  ñây là la

chn s liu ñ tính toán. Tính s trung bình trong 3 năm, 5 năm hay 10 năm? không có mt

qui tc tr li nào cho câu hi này và s la chn ph thuc vào ưc lưng ch quan ca

ngưi ra quyt ñnh.

Hai là, phương pháp s trung bình hiu ch nh. Có 2 vn ñ cn x! lý khi s! dng h

thng này. Th* nht, s! dng s liu bao nhiêu năm? Hai là, s! dng h thng hiu ch nh

nào là tt nht ?. Ngưc li, ch có kinh nghim, kh năng phán ñoán và s thích ca ngưi

ra quyt ñnh cùng vi s hiu bit v s liu mi cung cp cho chúng ta nh(ng hưng d%n

d/ dàng áp dng.

Bng 3.1 là mt ví d ñơn gin áp dng 2 phương pháp trên. Giá kỳ vng ñưc xác

ñnh theo phương pháp s bình quân ñơn gin là 2,96$, và theo phương pháp s bình quân

hiu ch nh là 3,11$, cao hơn s bình quân ñơn gin.



Trưng ði hc Nông nghip Hà Ni - Giáo trình Qan tr ri

ro -------------------------------------------------



Bng 3.1: Áp dng phương pháp s trung bình ñ th hin kỳ vng

Năm Giá trung bình hàng

năm ($)

H s hiu ch nh Giá x H s hiu

ch nh

4 năm trưc

3 năm trưc

2 năm trưc

1 năm trưc

T,ng cng

2,43

3,02

2,94

3,46

11,85

2,43

6,04

8,82

13,84

31,13

Giá tr kỳ vng

S trung bình ñơn gin 11,85 $ : 4 = 2,96$

S trung bình hiu ch nh 31,11$ :10 = 3,11$

b) Gía tr kỳ vng chc chn nht

Mt cách khác ñ biu th kỳ vng là chn giá tr có kh năng xy ra nht. Phương

pháp này cn có xác sut ca t"ng kt qu có kh năng xy ra. Kt qu có xác sut cao nht

s ñưc chn vì có kh năng xy ra nht. Ví d  bng 3.2 (hãy chưa nói ñn ct cui cùng)

áp dng phương pháp trên ñ biu th kỳ vng, thì năng sut 24t/ha s ñưc chn, vì có xác

sut cao nht do ñó có kh năng xy ra nht.

Bng 3.2: S! dng xác sut ñ xác ñnh kỳ vng

Năng sut có kh năng Xác sut Xác sut x Kt qu

T,ng s

0,1

0,3

0,4

0,2

1,0

1,2

5,4

9,6

6,0

22,2

Không chc rng năng sut này xy ra  mi năm, vì nu xác sut là chính xác thì trong dài

hn 40% thi gian s xy ra như vy.

c) Kỳ vng toán hc

Nu có xác sut (hoc ch quan hoc khách quan) ca các kt qu kỳ vng thì có th

tính kỳ vng toán hc. Kỳ vng toán hc là giá tr trung bình ca các kt qu thí nghim

hoc nhc li các s kin nhiu ln.

Phương pháp tính kỳ vng toán hc ñưc th hin  ct phi ca bng 3.3. Mi kt

qu có kh năng xy ra ñưc nhân vi xác sut ca nó và các kt qu ñưc cng li thành kỳ

vng toán hc. Cn chú ý là kỳ vng toàn hc  ñây là 22,2t/ha và nh hơn năng sut chc

chn nht (24t/ha) vì phân phi xác sut  ñây không ñi x*ng mà b lch v phía năng sut

thp. S liu  bng 3.2 th hin phân phi xác sut ri rc và không ñi x*ng mà lch v

phía năng sut thp. Chúng ta có th minh ha phân phi xác xut liên tc, không ñi x*ng

và lch v phía năng sut thp bng ñ' thi 3.2 dưi ñây. 0 ñ' th 3.2 giá tr M là giá tr hay

xy ra nht vì có xác sut ln nht, nhưng giá tr trung bình ca nó li nh hơn, vì phân phi

xác sut là phân phi lch (không phi phân phi chu1n), và giá tr trung bình là giá tr A.

Quản trị rủi ro trong các cơ sở sản xuất kinh doanh nông nghiệp: Phần 2

Chủ đề:

Tài liệu liên quan

Tài liêu mới

Hỗ trợ

Phương thức thanh toán

Theo dõi chúng tôi