
© Harry Campbell & Richard Brown
School of Economics
The University of Queensland
BENEFIT-COST ANALYSIS
BENEFIT-COST ANALYSIS
Financial and Economic
Financial and Economic
Appraisal using Spreadsheets
Appraisal using Spreadsheets
Chapter 9: Risk Analysis

In the preceding chapters we assumed all costs and benefits are
known with certainty.
The future is uncertain:
• factors internal to the project
• factors external to the project
Risk and Uncertainty
Where the possible values could have significant impact on project’s
profitability, a decision will involve taking a risk.
In some situations, degree of risk can be objectively determined.
Estimating probability of an event usually involves subjectivity.

Risk and Uncertainty
In risk analysis different forms of subjectivity need to be addressed
in deciding:
• what the degree of uncertainty is;
• whether the uncertainty constitutes a significant risk;
• whether the risk is acceptable.
Establishing the extent to which the outcome is sensitive to the
assumed values of the inputs:
• it tells how sensitive the outcome is to changes in input values;
• it doesn’t tell us what the likelihood of an outcome is.
Sensitivity Analysis
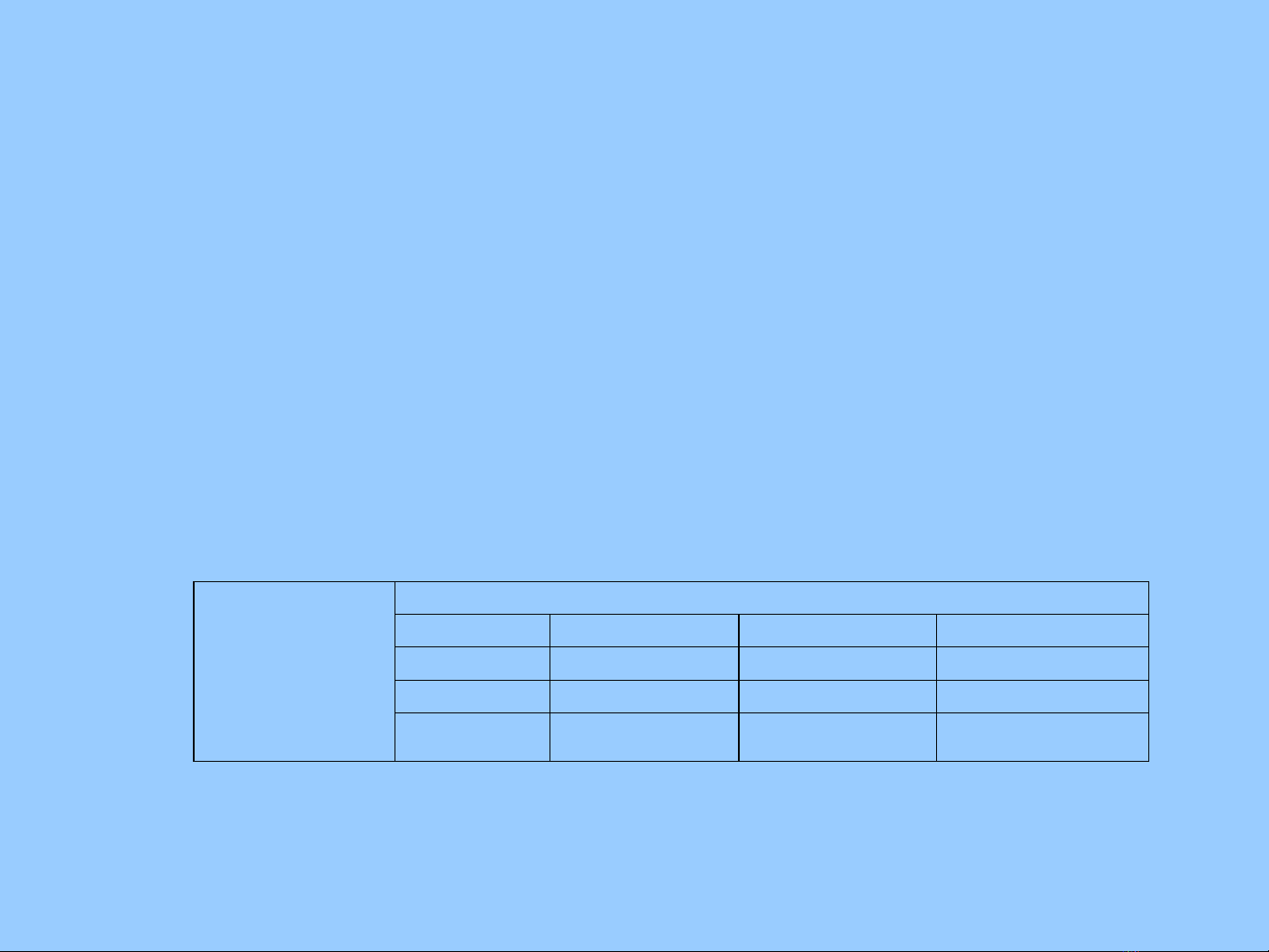
Table 9.1: Sensitivity Analysis Results: NPVs for Hypothetical Road Project
($ millions at 10% discount rate)
Construction Costs
75% 100% 125%
High $50 $40 $30
Medium $47 $36 $25
Road
Usage
Benefits Low $43 $32 $20

Risk modeling is the use of discrete probability distributions to
compute expected value of variable rather than point estimate.
Risk Modeling


























