A. M ĐUỞ Ầ
I. LÝ DO CH N Đ TÀIỌ Ề
Trong công cu c đi m i căn b n và toàn di n n n giáo d c n c nhà,ộ ổ ớ ả ệ ề ụ ướ
đi m i ph ng pháp d y h c là m t trong nh ng nhi m v quan tr ng hàngổ ớ ươ ạ ọ ộ ữ ệ ụ ọ
đu.ầ
Trong quá trình công tác, tr i qua nhi u ph ng pháp d y h c tích c c tôiả ề ươ ạ ọ ự
nh n th y ph ng pháp d y h c “Phát hi n và gi i quy t v n đ” có nhi u uậ ấ ươ ạ ọ ệ ả ế ấ ề ề ư
đi m cũng nh phù h p v i công tác gi ng d y b môn Toán tr ng phể ư ợ ớ ả ạ ộ ở ườ ổ
thông nói chung và d y h c bài t p toán nói riêng. Tuy nhiên đ có thành côngạ ọ ậ ể
trong ph ng pháp d y h c “Phát hi n và gi i quy t v n đ” ngoài năng l cươ ạ ọ ệ ả ế ấ ề ự
chuyên môn và năng l c s ph m c a m i giáo viên còn đòi h i ng i giáoự ư ạ ủ ỗ ỏ ở ườ
viên nhi u th i gian và tâm huy t.ề ờ ế
Đ có m t bài gi ng thu hút đc h c trò, giúp h c trò phát tri n t duyể ộ ả ượ ọ ọ ể ư
v môn toán và d n d t h c trò t i ni m say mê tìm tòi sáng t o, tôi th ng trănề ẫ ắ ọ ớ ề ạ ườ
tr v i nh ng khó khăn c a h c trò trong quá trình ti p c n t ng bài toán.ở ớ ữ ủ ọ ế ậ ừ
Bài toán hình h c gi i tích trong m t ph ng là bài toán th ng xu t hi nọ ả ặ ẳ ườ ấ ệ
các kì thi vì v y nó luôn đc s quan tâm đc bi t đi v i h c trò, bên c nhở ậ ượ ự ặ ệ ố ớ ọ ạ
đó nó cũng là bài toán khó v i nhi u đi t ng h c trò đc bi t là v i các em cóớ ề ố ượ ọ ặ ệ ớ
năng l c trung bình. Băn khoăn tr c nh ng khó khăn c a h c trò, tôi tìm tòi vàự ướ ữ ủ ọ
quy t đnh ch n ph ng pháp d y h c “Phát hi n và gi i quy t v n đ” đế ị ọ ươ ạ ọ ệ ả ế ấ ề ể
giúp các em ti p c n lo i toán này m t cách hi u qu nh t.ế ậ ạ ộ ệ ả ấ
Trong s nh ng bài toán v hình gi i tích trong m t ph ng có m t l p cácố ữ ề ả ặ ẳ ộ ớ
bài toán thiên v tính ch t hình ph ng thu n túy đã gây cho h c trò nhi u khóề ấ ẳ ầ ọ ề
khăn khi ti p c n. Vì v y tôi ch n đ tài là “Phát hi n và gi i quy t v n đế ậ ậ ọ ề ệ ả ế ấ ề
trong bài toán hình gi i tích t nh ng m i quan h gi ã các đi m, đi m vàả ừ ữ ố ệ ư ể ể
đng th ng” đ nghiên c u.ườ ẳ ể ứ
II. M C ĐÍCH NGHIÊN C UỤ Ứ
Tìm hi u nh ng khó khăn và thu n l i c a h c sinh khi ti p c n bài toánể ữ ậ ợ ủ ọ ế ậ
hình gi i tích trong m t ph ng thông qua ph ng pháp d y h c: “Phát hi n vàả ặ ẳ ươ ạ ọ ệ
gi i quy t v n đ”.ả ế ấ ề
III. ĐI T NG NGHIÊN C UỐ ƯỢ Ứ
- H c sinh kh i 10, 11 tr ng THPT Đông S n Iọ ố ườ ơ
- H c sinh kh i 12 ôn thi vào các tr ng đi h c tr ng THPT Đông S nọ ố ườ ạ ọ ườ ơ
I
IV. PH NG PHÁP NGHIÊN C UƯƠ Ứ
- Tìm ki m tài li u tham kh o t nhi u ngu n khác nhau liên quan đnế ệ ả ừ ề ồ ế
hình h c ph ng.ọ ẳ
- Trao đi v i các đng nghi p đ đ xu t bi n pháp th c hi n.ổ ớ ồ ệ ể ề ấ ệ ự ệ
1
- Gi ng d y các ti t bài t p toán t i các l p 11a2, 12a2 tr ng THPTả ạ ế ậ ạ ớ ườ
Đông S n I đ n m b t tình hình th c t c a h c sinh.ơ ể ắ ắ ự ế ủ ọ
B. N I DUNGỘ
I. C S LÍ LU N C A SÁNG KI N KINH NGHI MƠ Ở Ậ Ủ Ế Ệ
1. M t s đi m c n l u ýộ ố ể ầ ư
1.1. Nh ng bài toán liên quan đn tam giác vuông (đc bi t là tam giác vuôngữ ế ặ ệ
cân), hình ch nh t (đc bi t là hình vuông), hình thang vuông thì ta có th đtữ ậ ặ ệ ể ặ
m t c nh b ng a. T đó s d ng gi thi t, đnh lý Pitago, đnh lý hàm sộ ạ ằ ừ ử ụ ả ế ị ị ố
côsin… s xác đnh đc các y u t c n thi t thu n l i cho vi c gi i quy t bàiẽ ị ượ ế ố ầ ế ậ ợ ệ ả ế
toán đó. Bài toán c b n v kho ng cách và bài toán c b n v góc cũng th ngơ ả ề ả ơ ả ề ườ
đc s d ng trong ch đ này.ượ ử ụ ủ ề
1.2. V hình chính xác, t đó d đoán xem có hai đng th ng nào vuông gócẽ ừ ự ườ ẳ
v i nhau hay không. T đó s d ng đnh lý Pitago, ph ng pháp vect hay c ngớ ừ ử ụ ị ươ ơ ộ
góc đ ch ng minh d đoán này. Vi c phát hi n ra y u t vuông góc có th làể ứ ự ệ ệ ế ố ể
m u ch t đ chúng ta gi i quy t bài toán.ấ ố ể ả ế
1.3. S d ng đnh lý Talet, tam giác đng d ng đ so sánh kho ng cách t 2ử ụ ị ồ ạ ể ả ừ
đi m đn m t đng th ng. T đó s d ng bài toán c b n v kho ng cáchể ế ộ ườ ẳ ừ ử ụ ơ ả ề ả
ho c ph ng pháp tham s hóa đ gi i quy t bài toán.ặ ươ ố ể ả ế
2. M t s tính ch t c a hình h c ph ng v n d ng vào bài toánộ ố ấ ủ ọ ẳ ậ ụ
ph ng pháp t a đ trong m t ph ngươ ọ ộ ặ ẳ
Tính ch t 1ấ. Các h th c l ng trong tam giác vuông.ệ ứ ượ
Tính ch t 2.ấ Đnh lý hàm s cosin, h qu đnh lý hàm s cosin, đnh lý hàm sị ố ệ ả ị ố ị ố
sin, h qu đnh lý hàm s cosin, công th c trung tuy n, công th c tính di n tíchệ ả ị ố ứ ế ứ ệ
tam giác.
Tính ch t 3ấ. Cho hình vuông ABCD G i ọM, N l n l t là trung đi m c a ầ ượ ể ủ AB và
BC Khi đó AN
DM
Ch ng minh.ứ G i c nh hình vuông là ọ ạ
.a
Ta có
()()
2 2
.
. . . .
0 0 0.
2 2
A N DM A B BN DA A M
A B DA A B A M BN DA BN A M
a a
= + +
= + + +
= + − + =
uuuur uuuur uuur uuur uuur uuuur
uuur uuur uuur uuuur uuur uuur uuur uuuur
Suy ra
⊥.A N DM
N
M
D
C
B
Ch ng minh hoàn toàn t ng t nh trên ta có tính ch t sauứ ươ ự ư ấ
2
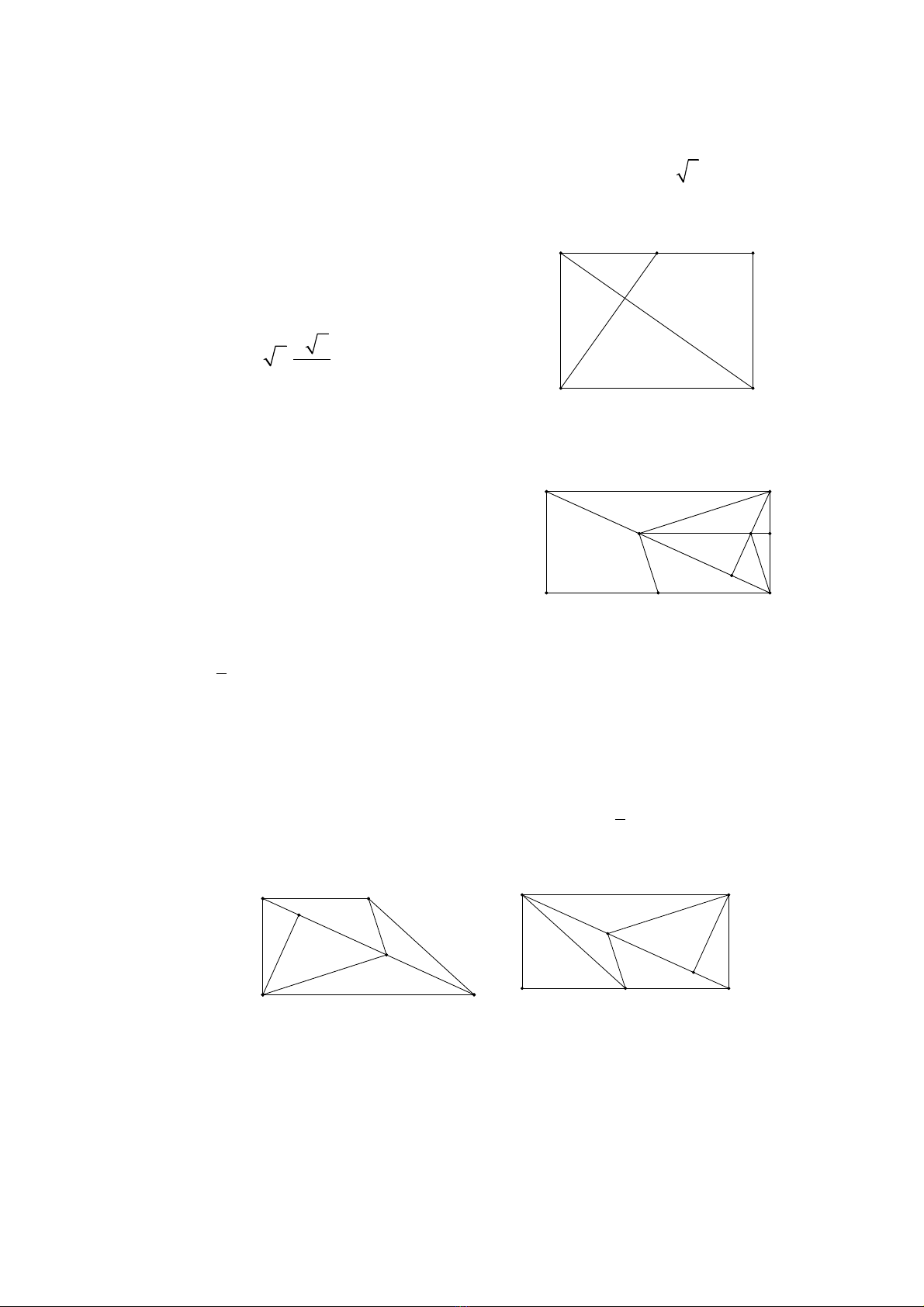
Tính ch t 4ấ. Cho hình vuông
.A BCD
G i ọ
,M N
l n l t thu c ầ ượ ộ
A B
và
BC
sao
cho
=
uuuur uuuur
,A M kA B
=
uuur uuur
.BN kBC
Khi đó
⊥.A N DM
Tính ch t 5ấ. Cho hình ch nh t ữ ậ
A BCD
có
= =, 2.A B a A D a
G i ọ
M
là trung
đi m ể
.A D
Khi đó
⊥.A C BM
Ch ng minh.ứ Ta có
( ) ( )
2
2
.
. . .
2
0 0 2. 0.
2
AC BM AB BC BA AM
AB AB AM BC BA BC AM
a
a a
= + +
= − + + +
= − + + + =
uuur uuuur uuur uuur uuur uuuur
uuur uuuur uuur uuur uuur uuuur
Suy ra
⊥.A C BM
M
A
B
C
D
Tính ch t 6ấ. Cho hình ch nh t ữ ậ
.A BCD
G i ọ
H
là hình chi u c a ế ủ
B
lên
A C
và
,M N
l n l t là trung đi m c a ầ ượ ể ủ
, .A H CD
Khi đó
⊥.BM MN
Ch ng minh.ứ G i ọ
E
là tr c tâmự
c a tam giác ủ
.MBC
Khi đó
/ /ME A B
(vì cùng vuông góc v iớ
).BC
Do
M
là trung đi m ể
A H
nên
ME
là đng trung bình c a tamườ ủ
giác
.HA B
Suy ra
E
A
B
C
D
H
M
N
1
/ / / /
2
ME A B ME NC= =�
Suy ra
MECN
là hình bình hành
/ / .MN CE
Vì
E
là tr c tâm c a tam giác ự ủ
MBC
nên
⊥ ⊥�.BM CE BM MN
Thay đi hình th c c a tính ch t 4 ta có các h qu sauổ ứ ủ ấ ệ ả
6.1. Cho hình thang
A BCD
vuông t i ạ
A
và
,D
=1.
2
A B CD
G i ọ
H
là hình chi uế
c a ủ
D
lên
A C
và
M
là trung đi m ể
.CH
Khi đó
⊥.MB MD
M
H
C
B
A
D
B
M
H
D
A
D
C
6.2. Cho tam giác
A BC
vuông t i ạ
B
có hai trung tuy n ế
BN
và
.CM
G i ọ
H
là
hình chi u c a ế ủ
B
lên
,CM
E
là trung đi m c a ể ủ
.CH
Khi đó
⊥.EN EB
3
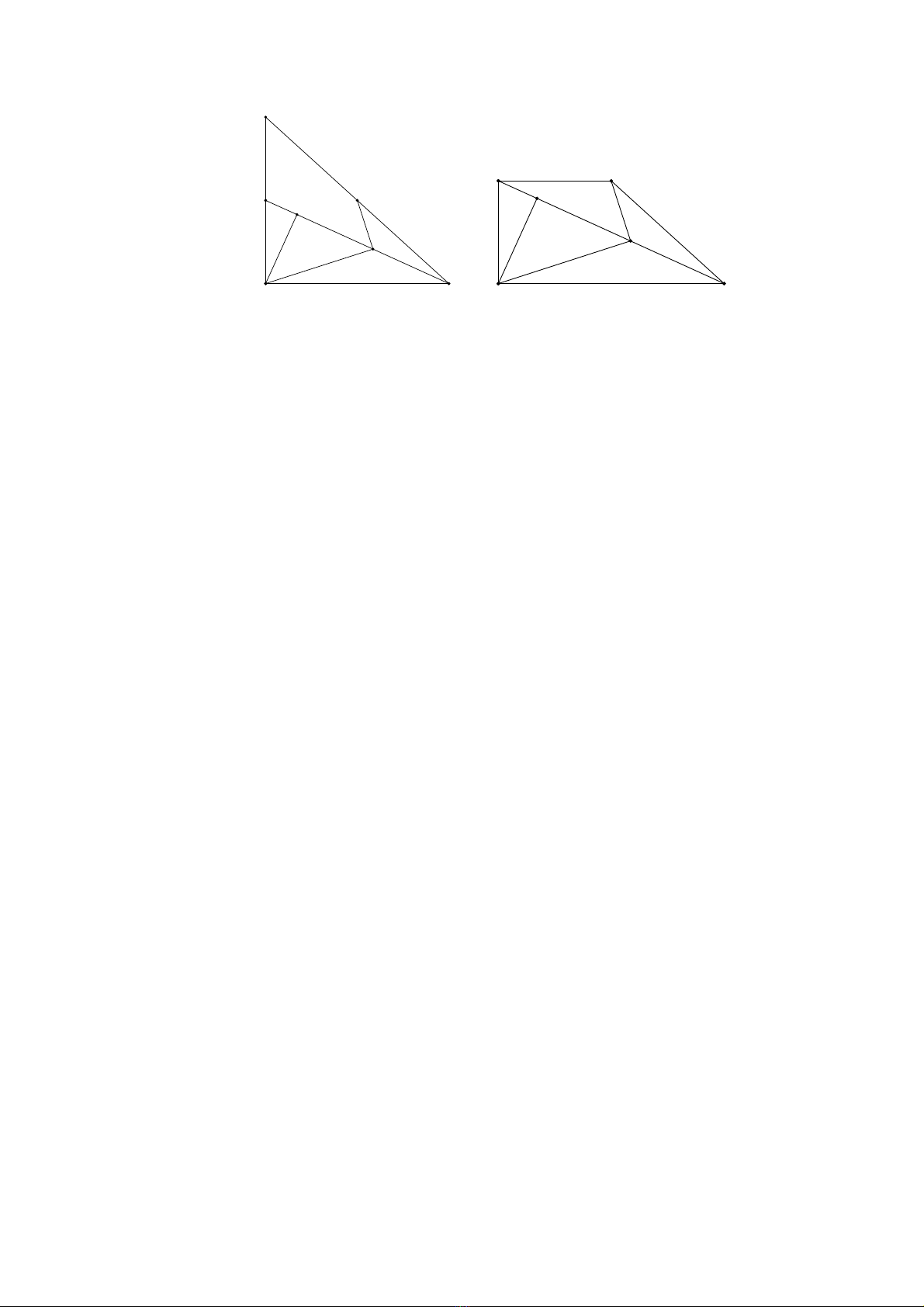
E
B
A
N
C
H
M
M
H
C
B
A
D
Trên đây là nh ng tính ch t đc khai thác nhi u trong các bài toán. ữ ấ ượ ề
II. TH C TR NG V N Đ TR C KHI ÁP D NGỰ Ạ Ấ Ề ƯỚ Ụ
- Ki n th c c s v môn toán c a các em h u h t t p trung m c đế ứ ơ ở ề ủ ầ ế ậ ở ứ ộ
trung bình.
- K t qu kh o sát m t s l p trong ph n gi i bài t p toán v ph nế ả ả ở ộ ố ớ ầ ả ậ ề ầ
hình gi i tích trong m t ph ng cũng nh qua tìm hi u các giáo viên d y bả ặ ẳ ư ể ở ạ ộ
môn toán, ch có kho ng 10% h c sinh h ng thú v i bài toán hình gi i tích trongỉ ả ọ ứ ớ ả
m t ph ng.ặ ẳ
III. GI I PHÁP ĐÃ TH C HI N Đ GI I QUY T V N ĐẢ Ự Ệ Ể Ả Ế Ấ Ề
Đa ra các bài toán c th trong các ti t d y h c bài t p, phân tích t ngư ụ ể ế ạ ọ ậ ừ
bài toán c th đ đnh h ng cho h c sinh cách gi i quy t bài toán và nh ngụ ể ể ị ướ ọ ả ế ữ
bài mang tính ch t t ng t .ấ ươ ự
IV. HI U QU C A SÁNG KI N KINH NGHI MỆ Ả Ủ Ế Ệ
- Sau khi áp d ng k t qu nghiên c u c a đ tài, qua vi c ki m tra kh oụ ế ả ứ ủ ề ệ ể ả
sát cho th y có trên 70% các em h c sinh có h ng thú v i bài h c và trong s đóấ ọ ứ ớ ọ ố
có kho ng 40% các em h c sinh bi t cách v n d ng m t cách linh ho t, nh t làả ọ ế ậ ụ ộ ạ ấ
s các em đang chu n b thi vào các tr ng đi h c.ố ẩ ị ườ ạ ọ
- Đ tài có th làm tài li u tham kh o cho các em h c sinh đang h c kh iề ể ệ ả ọ ọ ố
10 cũng nh các em h c sinh kh i 12 THPT đang ôn thi vào các tr ng đi h cư ọ ố ườ ạ ọ
và cao đngẳ
V. BÀI T P ÁP D NG Ậ Ụ
-Trong khuôn kh c a đ tài, sau đây tôi xin trình bày m t s bài toán hìnhổ ủ ề ộ ố
h c gi i tích ph ng liên quan đn tam giác vuông, hình thang vuông, hình chọ ả ẳ ế ữ
nh t và hình vuông.ậ
- m i bài toán đu có s phân tích bài toán và đa ra h ng gi i đỞ ỗ ề ự ư ướ ả ể
giúp các em h c sinh ti p c n bài toán m t cách d dàng h n, qua đó h c sinh cóọ ế ậ ộ ễ ơ ọ
th v n d ng cho nh ng bài toán t ng tể ậ ụ ữ ươ ự
4
Bài 1. Trong m t ph ng v i h tr c t a đ ặ ẳ ớ ệ ụ ọ ộ
,Oxy
cho hình thang ABCD vuông
t i ạA và B.
( )
−9; 1M
là trung đi m ểAB,
− − =: 2 4 0.CD x y
Tìm to đ c a ạ ộ ủ C bi tế
r ng ằ
= = 3.
2
A B BC A D
Phân tích bài toán. Bài toán này chúng ta có th đi theo m t trong các h ngể ộ ướ
nh sau:ư
H ng th nh t.ướ ứ ấ Vì
C CD
nên ta tham s hóaố
đi m ểC ( n ẩc). Hình thang
vuông này có các c nh liênạ
h v i nhau qua đng th cệ ớ ẳ ứ
= = 3,
2
A B BC A D
nên n uế
đt đ dài m t c nh nàoặ ộ ộ ạ
đó b ng ằx thì ta s tínhẽ
đc t t c các c nh cònượ ấ ả ạ
l i theo ạx.
Đ tìm ểC, ta s đi tính đẽ ộ
dài đo n th ng ạ ẳ MC. Chú ý
r ng ằ
( )
,d M CD
đã có.
4
x
2
x
3
x
3
x
4
x
2
x
y
4 = 0
M
9;
1
( )
H
K
D
C
B
A
L i gi iờ ả . Đt ặ
=6 .A B x
Suy ra
=6 ,BC x
AD =4x. Do đó
=2 10.CD x
Ta có
( )
=, 3 5.d M CD
Suy ra
=15 2.
MCD
S x
M t khácặ
2
4 6 3 .4 3 .6
.6 15 .
2 2 2
MCD
x x x x x x
S x x
+
= − − =
Suy ra
=2.x
Suy ra
= =3 5 3 10.MC x
Vì
( )
− − = −� �: 2 4 0 ; 2 4 .C CD x y C c c
Khi đó
( ) ( )
=
= − + − =� � =
2 2
0
3 10 9 2 3 90 .
6
c
MC c c c
T đó suy ra ừ
( ) ( )
−0; 4 , 6; 8 .C C
H ng th hai.ướ ứ N u vi t đc ph ng trình c a đng th ng ế ế ượ ươ ủ ườ ẳ
MC
thì s tìmẽ
đc t a đ c a ượ ọ ộ ủ
.C
Ta s tìm cách tính ẽ
ﾷ
cos ,MCD
t đó s d ng bài toán c b nừ ử ụ ơ ả
v góc.ề
L i gi iờ ả . Đt ặ
=6 .A B x
Suy ra
=6 ,BC x
AD = 4x. Do đó
= = =2 10, 5 , 3 5 .CD x MD x MC x
Áp d ng đnh lý hàm s cosin cho tam giác ụ ị ố MCD ta có
5