TOÁN 10-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG Điện thoại: 0946798489
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
PHẦN 1. LÝ THUYẾT – VÍ DỤ
Bài 1. Mệnh đề
A - Kiến thức cần nhớ
- Mệnh đề là một câu nhận giá tri đúng hoặc sai, nhưng không phải cả hai. Định lí là một mệnh đề đúng và
thường có dạng
P Q
, trong đó
P
là mệnh đề đúng.
- Mệnh đề "Nếu
P
thì
Q
" là mệnh đề kéo theo, kí hiệu là
P Q
.
Trong định lí có dạng
P Q
, ta gọi
P
là giả thiết,
Q
là kết luận của định lí. Khi mệnh đề kéo theo đúng,
thì người ta gọi
P
là điều kiện đủ đề có
Q
;
Q
là điều kiện cần đề có
P
.
Mệnh đề
Q P
được gọi là mệnh đề đảo của mệnh đề
P Q
.
- Mệnh đề "
P
nếu và chỉ nếu
Q
" được gọi là một mệnh đề tương đương và kí hiệu là
P Q
.
Nếu cả hai mệnh đề
P Q
và
Q P
đều đúng thì mệnh đề
P Q
là một mệnh đề đúng.
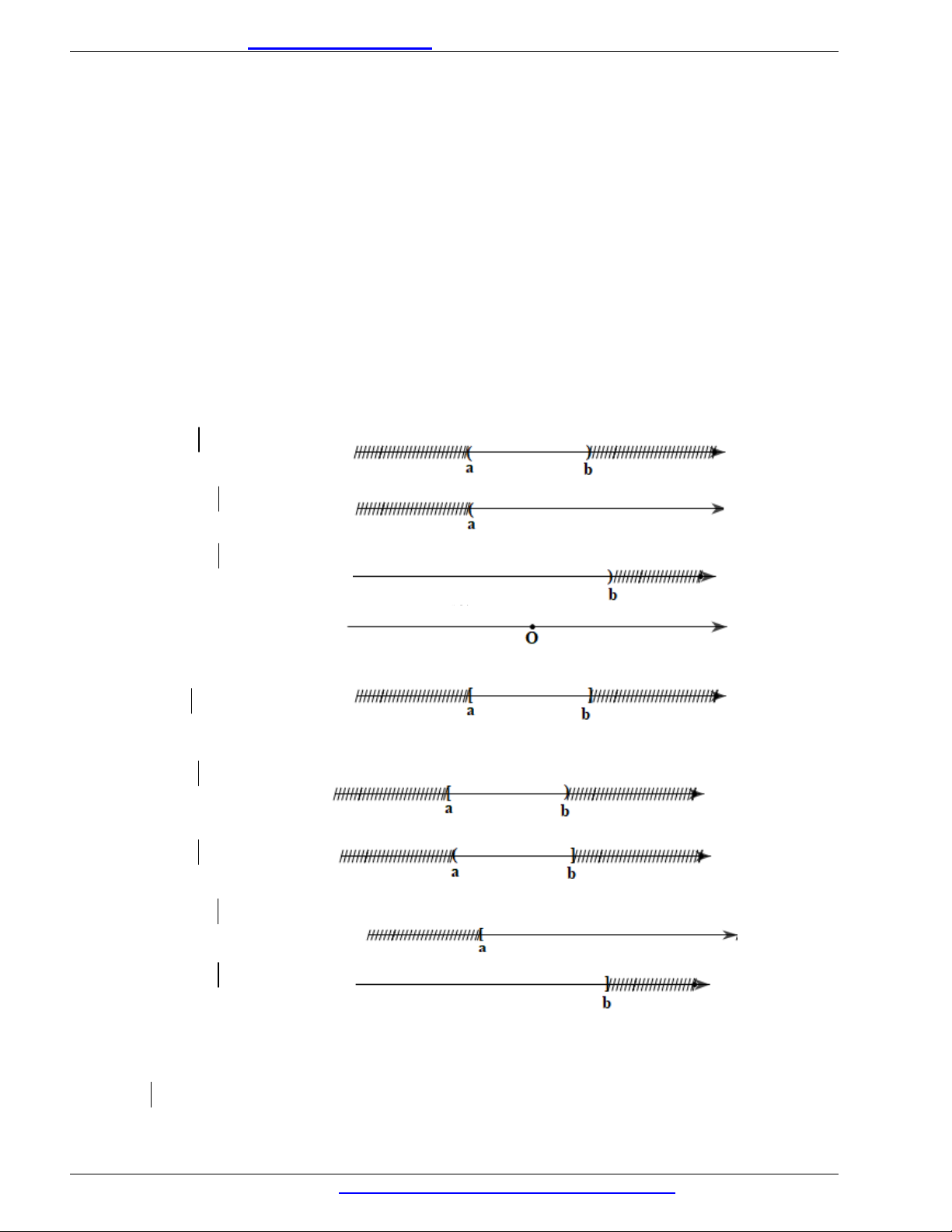
- Phát biểu "
, ( ) x X P x
" là một mệnh đề đúng nếu với bất kì
0 0
,x X P x
đúng và sai néu có một
0 0
,x X P x
sai.
Phát biều "
, ( ) x X P x
" là một mệnh đề đúng nếu có ít nhất một
0
x X
đề
0
P x
đúng và sai nếu với
0
x X
bất kì,
0
P x
sai.
- Phủ định của mệnh đề
P
là một mệnh đề, kí hiệu là P, đúng khi
P
sai và sai khi
P
đúng.
Phủ định của mệnh đề “
, ( ) x X P x
" là mệnh đề "
, ( ) x X P x
".
Phủ định của mệnh đề "
, ( ) x X P x
" là mệnh đề "
, ( ) x X P x
".
B - Ví dụ
Ví dụ 1. Trong các câu sau, câu nào là mệnh đề? Câu nào không là mệnh đề? Xác định tính đúng sai của các
mệnh đề.
a) Hình vuông có hai đường chéo vuông góc với nhau.
b) Sông Hương chảy ngang qua thành phố Huế.
c) Năm 2022 không phải là năm nhuận.
d) Hôm nay trời đẹp quá!
e)
3 2 5 x
g)
4 6 5
Giải
Những câu
, , ,a b c g
là mệnh đề. Các câu
, ,abc
là những mệnh đề đúng, câu
g
là mệnh đề sai.
Câu d là câu cảm thán, không phải là mệnh đề. Câu e không xác định được tính đúng sai, không phải là
mệnh đề (câu e là mệnh đề chứa biến).
Ví dụ 2. Cho mệnh đề
: 2 "P
là số hữu tỉ". Hãy phát biểu mệnh đề phủ định của mệnh đề
P
.
Giải
Mệnh đề
Q
: "
2
không phải là số hữu tỉ" nhận được từ mệnh đề
P
bằng cách thêm cụm từ "không phải"
trước vị ngữ. Mệnh đề
Q
là mệnh đề phủ đinh của mệnh đề
P
.
Vì với mổi số thực chỉ xảy ra một trong hai trường hợp: là số hữu tỉ hoặc là số vô tỉ, không có trường hợp
khác. Do vậy khi viết "
2
không phải là số hữu tì" së cùng nghĩa với "
2
là số vô tỉ". Vì vậy mệnh đề
R
:
"
2
là số vô tỉ" cũng là mệnh để phủ định của mệnh đề
P
.
Vậy cả hai mệnh đề
Q
và
R
đều là các mệnh đề phủ định của mệnh đề
P
.
Ví dụ 3. Cho hai mệnh đề sau:
P
: "Tứ giác
ABCD
là hình thoi" và
Q
: "Tứ giác
ABCD
có hai đường chéo vuông góc".
ÔN TẬP CHƯƠNG 1. MỆNH ĐỀ - TẬP HỢP
•TOÁN 10
•|FanPage: Nguyễn Bảo Vương
Blog: Nguyễn Bảo Vương:
https://www.nbv.edu.vn/
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Hãy phát biểu mệnh đề
P Q
.
Giải
Mệnh đề
P Q
: "Nếu tứ giác
ABCD
là hình thoi thì tứ giác
ABCD
có hai đường chéo vuông góc".
Bài 2. Tập hợp
A - Kiến thức cần nhớ
1. Tập hợp
- Tập hợp là một khái niệm cơ bản của toán học. Chúng ta có thề cho một tập hợp bằng cách liệt kê các phần
tử hoặc chỉ ra tính chất đặc trưng cho các phẩn tử của tập hợp đó.
- Tập hợp không chứa phần tử nào được gọi là tập rỗng, kí hiệu là
.
- Tập hợp
A
được gọi là tập hợp con của tập hợp
B
nếu mọi phần tử của tập hợp
A
đều là phần tử của tập
hợp
B
. Kí hiệu là
A B
.
Tập rô
ng là tập con của mọi tập hợp và tập hợp
A
là tập hợp con của chính nó.
- Hai tập hợp
A
và
B
được gọi là hai tập hợp bằng nhau nếu mỗi phần tử của
A
cũng là phần tử của
B
và
ngược lại. Kí hiệu là
A B
.
2. Các tập con thường dùng của
- Khoảng
( ; ) { }a b x a x b
( ; ) { }a x a x
( ; ) { }b x x b
( ; ) 
- Đoạn
[ ; ] { }a b x a x b
- Nứa khoảng
[ ; ) { }a b x a x b
( ; ] { }a b x a x b
[ ; ) { }a x a x
( ; ] { }b x x b
3. Các phép toán trên tập hợp bao gồm: phép hợp, phép giao và hiệu của hai tập hợp.
- Giao của hai tập hợp
A
và
B
, kí hiệu là
A B
, là một tập hợp chứa các phần tử thuộc cả tập hợp
A
và
tập hợp
B
.
{ }.A B x x A vaøx B
- Hợp của hai tập hợp
A
và
B
, kí hiệu là
A B
, là một tập hợp chứa các phần tử hoặc thuộc tập hợp
A
hoặc thuộc tập hợp
B
.
Điện thoại: 0946798489 TOÁN 10-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
{ hoaëc }. A B x x A x B
- Tập hợp gồm các phần tử thuộc
A
nhưng không thuộc
B
gọi là hiệu của hai tập hợp
A
và
B
. Kí hiệu là
\A B
.
\ { vaø }.A B x x A x B
- Khi
B A
thì
\A B
gọi là phần bù của
B
trong
A
, kí hiệu là A
C B
.
B - Ví dụ
Ví dụ 1. Xác định tính đúng sai của các mệnh đề sau:
a)
6
;
b) 2 ;
c)
0,368
d)
{3}
.
Giải
a)
6
là mệnh đề đúng.
b) 2 là mệnh đề sai.
c)
0,368
là mệnh đề đúng.
d)
{3}
là mệnh đề sai, vì kí hiệu
{3}
là tập hợp chứa phần tử là 3, đây là tập con của
N
, chứ không phải
là một phần tử của
N
(cách viết đúng là
{3}
).
Ví dụ 2. Cho G là tập hợp các số nguyên dương nhỏ hơn 10 là bội của 3 và
H
là tập hợp các nghiệm của
phương trình
2
7 10 0 x x
.
a) Hãy liệt kê các phần tử của hai tâp hợp
G
và
H
.
b) Tìm
( )n H
.
c) Biều diễn hai tập hợp
G
và
H
bằng biều đồ Ven.
Giải
a) Vì
G
là tập hợp các số nguyên dương là bợi của 3 và nhỏ hơn 10 nên
{3;6;9}G
.
Phương trình
2
7 10 0 x x
có hai nghiệm là
2x
và
5x
. Vậy
{2;5}H
.
b) Tử câu a ta thấy tập hợp
H
có 2 phần tử. Vậy
( ) 2n H
.
c) Biều diễn hai tập hợp
G
và
H
bằng biều đồ Ven.
Ví dụ 3. Cho hai tập hợp A, B được mô tả bởi biểu đồ Ven như sau:
a) Hãy chỉ ra các phần tử của tập hợp
A
.
b) Tinh
( )n A B
.
c) Hãy chỉ ra các phần tử thuộc tập hợp
A
mả không thuộc tập hợp
B
.
Giải
a)
{1;2;3;4;5}A
.
b)
{1;2;3;4;5;7;9;11} A B
. Tử đó suy ra
( ) 8 n A B
.
c) Các phần tử thuộc tập hợp
A
mà không thuộc tập hợp
B
là:
3;4;5
.
Ví dụ 4. Biều diễn các tập hợp sau trên trục số.
Blog: Nguyễn Bảo Vương:
https://www.nbv.edu.vn/
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
a)
[3;9] \[ 2;7) A
;
b)
[ 1; ) ( 4;9]  E
c)
[1;5] [4; ); C
d)
\[ 1; ) D
.
Giải
a)
[3;9] \[ 2;7) [7;9]
A
.
b)
[ 1; ) ( 4;9] [ 1;9]

B
.
c)
[1;5] [4; ) [1; )
 
C
.
d)
\[ 1; ) ( ; 1)
 
D
.
PHẦN 2. BÀI TẬP TỰ LUẬN
Câu 1. Tìm mệnh đề phủ định của mệnh đề sau:
2
, 1 0 x x
.
Câu 2. Tìm mệnh đề phủ định của mệnh đề sau:
2
: 7 0x x
.
Câu 3. Tìm mệnh đề phủ định của mệnh đề sau:
2
:3 2 1x x x
.
Câu 4. Cho tập hợp
3;3 15A x x x
. Số phần tử của tập hợp
A
là
Câu 5. Cho hai tập hợp
1;5;9;13;17;21;25A
và
0;1;3;5;10;13B
. Tìm
A B
.
Câu 6. Cho hai tập hợp
1;2;3;5;8A
và
1;0;1;5;9B
. Tìm
A B
.
Câu 7. Cho hai tập hợp
1;3;5;7
A
và
1;2;3;4
B
. Tìm
\A B
Câu 8. Cho mệnh đề
2
:“ , 2 5 0”P x x x
. Tìm mệnh đề phủ định của
P
Câu 9. Cho
;5A 
. Khi đó
?C A
Câu 10. Cho tập hợp
1; 2;3A
,
2
| 2 3 0B x x x
,
| 2 1 5C x x
. Khi đó
\ ?A C B
Câu 11. Cho các tập
A x x
,
| 4
B x x
. Tập
C A B
là :
Câu 12. Cho hai tập hợp khác rỗng
3;5A m
,
2;3 1B m
với
m
. Tìm
m
để
A B
.
Câu 13. Cho các mệnh đề sau:
(1) Mọi số tự nhiên chia hết cho
2
và
3
thì chia hết cho
6
.
(2) Với a:
3 9a a
.
(3) Trong tam giác vuông bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
(4) : 2 1
n
n là số nguyên.
(5)
2
: 0n n
.
(6) Một tam giác là tam giác vuông khi và chỉ khi đường trung tuyến ứng với cạnh huyền bằng
một nửa cạnh huyền.
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
Câu 14. Cho hai tập hợp
( ;6]A m
,
(4;2021 5 )B m
và A, B khác rỗng. Có bao nhiêu giá trị nguyên
của m để
\A B
?
Điện thoại: 0946798489 TOÁN 10-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Câu 15. Cho các tập hợp khác rỗng
2 1; 4
A m m
và
; 1 5;B

. Tìm tất cả các giá trị
thực của
m
để A B
Câu 16. Cho tập hợp
2
| 1 4
A x x
,
2
| 1 0B m x mx m
coù hai nghieäm traùi daáu
. Tập hợp
\A B
có tất cả bao nhiêu tập
hợp con?
Câu 17. Ở lớp 10A, mỗi học sinh đều có thể chơi được ít nhất 1 trong 3 môn thể thao là cầu lông, bóng đá
và bóng chuyền. Có 11 em chơi được bóng đá, 10 em chơi được cầu lông và 8 em chơi được bóng
chuyền. Có 2 em chơi được cả 3 môn, có 5 em chơi được bóng đá và bóng chuyền, có 4 em chơi
được bóng đá và cầu lông, có 4 em chơi được bóng chuyền và cầu lông. Hỏi lớp học có bao nhiêu
học sinh?
Câu 18. Cho các tập hợp sau:
| 1 2
A x x
;
2
| 3 0
B x x x
. Tìm tập hợp
\
C A B A B
Câu 19. Cho hai tập hợp
4 3 2
4 3 0
A x x x x
và
5 3
2 0
B x x x x
Tìm số tập
hợp
X
có ba phần tử trong đó có đúng một phần tử dương thỏa mãn
\
A B X A B
Câu 20. Cho hai tập hợp
4;18
A m
và
2;2 10
B m
khác tập hợp rỗng (
m
là tham số). Tìm tất cả
các giá trị thực của tham số
m
để
B A
.
Câu 21. Trong các mệnh đề sau, có bao nhiêu mệnh đề đúng ?
P: “Với mọi số tự nhiên
n
và
3
n
chia hết cho 3 thì
n
chia hết cho 3”.
Q: “
2
, 1
n n
chia hết cho
4
”.
K: “Cho
, ,a b c
dương thỏa mãn
1abc
. Nếu
1 1 1
a b c
abc
thì có một và chỉ một trong ba
số
, ,a b c
lớn hơn một”.
L : “Nếu phương trình bậc hai
2
0
ax bx c
vô nghiệm thì
a
và
c
cùng dấu.”
Câu 22. Cho các tập
2 2
: 2 1 0
A x x m x m m
,
2 1;3
B m
là các tập khác
và tập
: 3
C x x
,
0;4
D
. Số các giá trị nguyên của
m
sao cho
A B C D
?
Câu 23. Lớp 10A có
21
em thích học Toán,
19
em thích học Văn và có
18
em thích học tiếng Anh. Trong
số đó có
9
em thích học cả Toán lẫn Văn,
7
em thích học cả Văn lẫn tiếng Anh,
6
em thích học
cả Toán lẫn tiếng Anh và có
4
em thích học cả ba môn Toán, Văn, Anh, không có em nào không
thích một trong ba môn học trên. Hỏi trong lớp 10A có bao nhiêu học sinh?
Câu 24. Cho tập
| 2 1 3
A n n
chia heát cho
,
| 1 gB khônn n
chia heát cho 4
,
;2023
C 
. Tìm số phần tử của tập
\
A B C
Câu 25. Cho tập
3;A

,
,
B x x m
. Có bao nhiêu giá trị nguyên của tham số
20;20
m
để tập hợp
\A B
có không quá 10 phần tử?
LỜI GIẢI THAM KHẢO
Câu 1. Tìm mệnh đề phủ định của mệnh đề sau:
2
, 1 0
x x
.
Lời giải
Phủ định của mệnh đề
2
, 1 0
x x
là:
2
, 1 0
x x
.
Câu 2. Tìm mệnh đề phủ định của mệnh đề sau:
2
: 7 0
x x
.
Lời giải