TOÁN 10-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG Điện thoại: 0946798489
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
PHẦN 1. LÝ THUYẾT – VÍ DỤ
Bài 5. Giá trị lượng giác của một góc từ
0
đến
180
A - Kiến thức cần nhớ
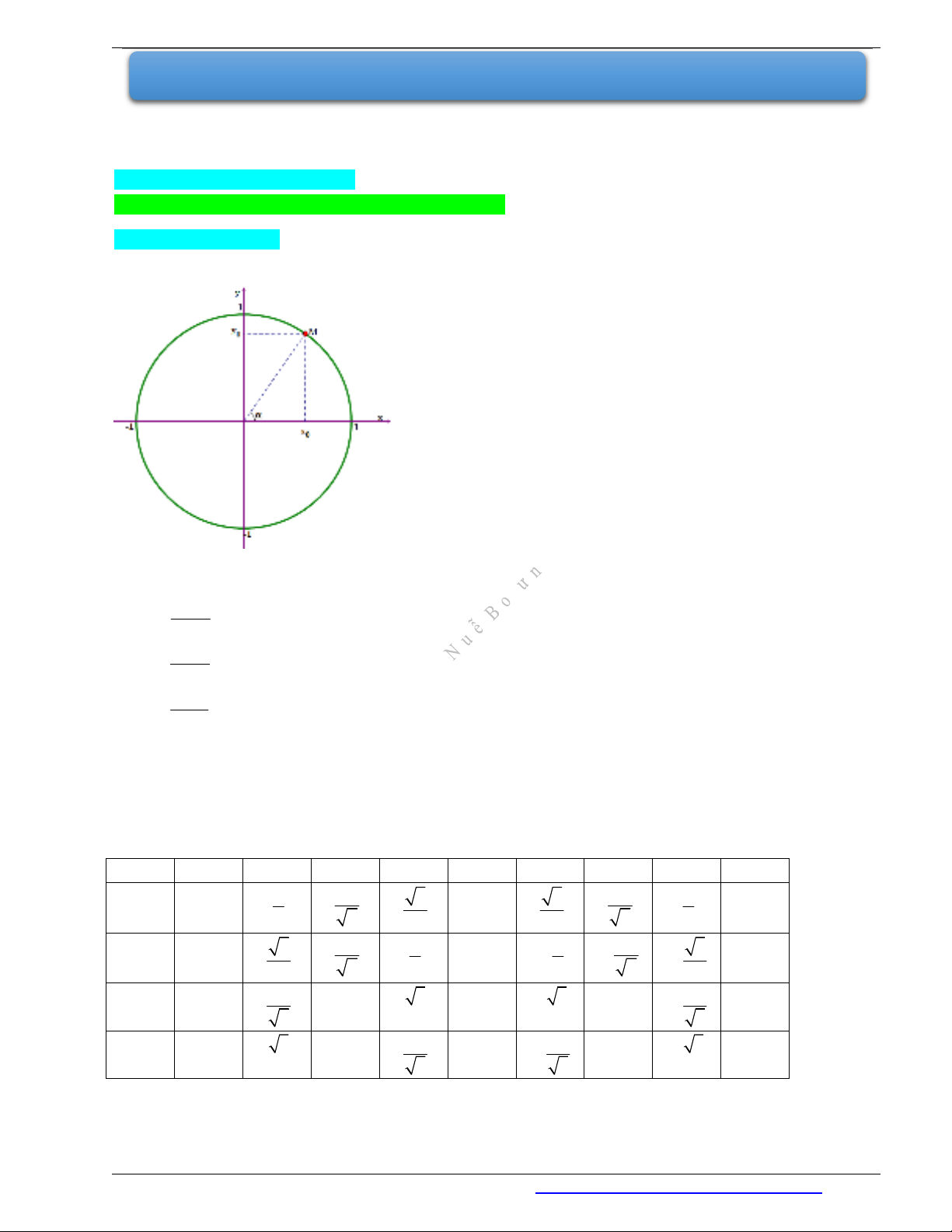
1. Điểm
0 0
;M x y
nầm trên nửa đường tròn đơn vị sao cho
XOM
Khi đó:
0 0
sin , cos
y x
,
sin
tan 90
cos
.
cos
cot 0 , 180
sin
.
1
tan 0 ;90 ;180 .
cot
2. Khi
0
thì
sin 0,cos 1
.
Khi
90
thì
sin 1,cos 0
.
Khi
0 90
thì
0 sin 1,0 cos 1
,
tan 0
và
cot 0
.
Khi
90 180
thì
0 sin 1, 1 cos 0
, tan
0
và
cot 0
.
3. Bảng giá trị lượng giác (GTLG) của một số góc đạc biệt cần nhớ
GTLG
0
30
45
60
90
120
135
150
180
sin
0
1
2
1
2
3
2
1
3
2
1
2
1
2
0
cos
1
3
2
1
2
1
2
0
1
2
1
2
3
2
1
tan
0
1
3
1
3
‖
3
1
0
cot
‖
3
1
1
3
0
1
3
‖
Bảng 3.1. Giá trị lượng giác của một số góc đặc biệt
4. Tính chất
a) Giá trị lượng giác của hai góc phụ nhau:
ÔN TẬP CHƯƠNG 3. HỆ THỨC LƯỢNG TRONG TAM GIÁC
•TOÁN 10
•|FanPage: Nguyễn Bảo Vương
Blog: Nguyễn Bảo Vương:
https://www.nbv.edu.vn/
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
sin 90 cos ,cos 90 sin
tan 90 cot ,cot 90 tan .
b) Giá trị lượng giác của hai góc bù nhau:
sin 180 sin , cos 180 cos
tan 180 tan , cot 180 cot .
c) Hệ thức cơ bản (bài tập 3.3, SGK Toán 10, tập một):
2 2
2
2
2
2
sin cos 1
1
1 tan 90
cos
1
1 cot 0 180 .
sin
tan cot 1 0 180 , 90 .
B - Ví dụ
Ví dụ 1. Không dùng máy tinh, tính giá trị của các biều thức sau:
a)
sin 45 cos135 cos60 sin150 cos30 sin120
A
;
b)
tan135 cot 60 cot 30 tan 60 tan150
B
c)
2sin 60 tan150 cos180 cot 45
C
.
Giải
a) Từ Bảng
3.1
ta thấy
1 1
sin 45 cos135 ,cos 60 sin150
2
2
và
3
cos30 sin120 .
2
Từ đó suy ra
1 1 1 1 3 3 1 1 3
1
2 2 2 2 2 4 4
2 2
A
.
b)
1 1
Do tan135 1,cot 60 ,cot 30 tan 60 3, tan150
3 3
nên
1 1
1 3 3 1
3 3
B
.
c) Cũng từ Bảng
3 1
3.1,sin 60 , tan150 ,cos180 1
23
và
cot 45 1
. Suy ra
3 1
2 ( 1) 1 0.
23
C
Chú ý. Nếu đề ý đến mối liên hệ giữa các góc có trong biểu thức, như các góc bù nhau, các góc phụ nhau,
thì ta có thể giải bài toán theo cách sau:
a) Do
135 180 45 ,150 180 30 ,120 180 60
nên
sin 45 cos 45 cos60 sin30 cos30 sin 60
1 1 1 1 3 3 1 1 3 1.
2 2 2 2 2 4 4
2 2
A
b) Do
135 180 45 ,60 90 30 ,150 180 30
nên
1 1 tan 60 tan 30 1.
B
c) Do
150 180 30
nên
3 1
2sin 60 tan30 cos180 cot 45 2 ( 1) 1 0.
23
C
Điện thoại: 0946798489 TOÁN 10-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Ví dụ 2. Cho góc
,0 180
thoả mãn
1
cos
3
.
a) Tính
tan .
b) Tính giá trị của biểu thức
tan 2cot
P
.
Giải
a) Do
1
cos 0
3
nên
là góc tù và
2
1
tan 1 2 2
cos
.
b) Do
tan cot 1
và tan
2 2
nên
1
cot
2 2
và bởi vậy
1 5
2 2 2
2 2 2
P
Nhận xét. Khi tính tan
từ
cos
nhờ đẳng thức
2
2
1
1 tan
cos
sai lầm thường gặp của học sinh là
mặc định coi 2
1
tan 1
cos
mà quên mất
tan 0
khi
là góc tù.
Bài 6. Hệ thức lượng trong tam giác
A - Kiến thức cần nhớ
Quy ước, kí hiệu. Với tam giác
ABC
, ta thường sử dụng các kí hiệu sau:
, ,a b c
: Độ dài các cạnh
, ,BC CA AB
, ,
abc
h h h
: Độ dài đường cao kẻ từ
, ,A B C
2
abc
p
: Nửa chu vi của tam giác
S
: Diện tích của tam giác
,
R r
: Bán kinh đường tròn ngoại tiếp, bán kính đường tròn nội tiếp
, ,
abc
m m m
: Độ dài đươong trung tuyến kẻ từ
, ,A B C
.
Định lí côsin. Trong tam giác
, ta có
2 2 2
2 cos
a b c bc A
.
Định lí sin. Trong tam giác
ABC
, ta có
2
sin sin sin
a b c
R
A B C
.
Các công thức tính diện tích:
1 1
sin ( )( )( ).
2 2 4
a
abc
S ah ab C pr p p a p b p c
R
B - Ví dụ
Ví dụ 1. Cho tam giác
có
8, 9, 6
a b c
.
a) Tính số đo các góc của tam giác.
b) Tính diện tích, bán kinh đường tròn ngoại tiếp, bán kính đường tròn nội tiếp. độ dài các đường cao của
tam giác.
Giải
a) Áp dụng định lí côsin, ta có
2 2 2
81 36 64 53
cos .
2 2 9 6 108
b c a
Abc
Suy ra
ˆ60 36 39

A
.
Hoàn toàn tương tự, tính được
ˆ
ˆ
78 35 5 , 40 4816
 
B C
.
b) Do
8, 9, 6
a b c
nên tam giác
có nửa chu vi
8 9 6 23
2 2
p
. Suy ra
7 5
,
2 2
p a p b
và
11
2
p c
. Từ đó, theo công thức Heron ta được diện tích của tam giác là
23 7 5 11 8855
2 2 2 2 4
S.
Blog: Nguyễn Bảo Vương:
https://www.nbv.edu.vn/
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Suy ra bán kinh đường tròn nội tiếp
8855
46
S
rp
và bán kinh đường tròn ngoại tiếp
432
4
8855
abc
RS
.
Nhận xét
- Định lí côsin giúp ta giải tam giác trong trường hợp biết ba cạnh của tam giác hoặc biết hai cạnh và góc
xen giữa hai cạnh đó (bài tập
3.8
và
3.9
).
- Từ
53
cos
108
A
, sử dụng hệ thức cơ bản (bài tập 3.3, SGK Toán 10, tập một), tính được
8855
sin
108
A
.
Từ đó, sử dụng công thức
1
sin
2
S bc A
ta cũng thu được
8855
4
S
.
Ví dụ 2. Cho tam giác
có
ˆ15 , 6
A c
và
ˆ
120
B
.
a) Tính độ dài các cạnh
,a b
.
b) Tính độ dài bán kính đường tròn ngoại tiếp tam giác và diện tích của tam giác.
c) Tính độ dài đường cao
a
h
.
Giải
a) Do
ˆˆ
15 , 120
A B
nên
ˆ ˆ
ˆ
180 45
C A B
.
Áp dụng đinh lí sin ta được:
6
.sin .sin15 3 3 1
sin sin 45
6
.sin .sin120 3 6
sin sin 45
c
a A
C
c
b B
C
b) Theo định lí sin, bán kính đường tròn ngoại tiếp của tam giác là
6
3 2.
2sin 2 sin 45
c
R
C
Do
3( 3 1), 3 6, 6
a b c
và
3 2
R
nên
3( 3 1) 3 6 6 9 3( 3 1) .
4 2
4 3 2
abc
SR
c) Từ kết quả của phần b), suy ra
2 9 3( 3 1)
3 3
3( 3 1)
a
S
ha
.
Nhận xét
- Định lí sin giúp ta giải tam giác trong trường hợp biết hai góc và một cạnh của tam giác.
- Ở phần b) cũng có thể sử dụng công thức
1
sin
2
S ab C
để tính diện tích của tam giác.
Ví dụ 3. Cho tam giác
. Chứng minh rằng:
a)
2 2 2
2
2 4
a
b c a
m
;
b)
1 1 1 1
abc
h h h r
.
Giải
a) Gọi
M
là trung điểm của
BC
. Khi đó
a
m AM
. Có hai trường hợp sau xảy ra:
Trường hợp 1.
b c
. Trong trường hợp này
AM
cũng chính là đường cao kẻ từ
A
của tam giác. Do đó
2 2 2 2
2 2 2 2
4 2 4
a
a b b a
m AC CM b
.
Trường hợp 2.
b c
. Không mất tính tổng quát, xét trường hợp
b c
, trường hợp còn lại chứng minh tương
tự.
Điện thoại: 0946798489 TOÁN 10-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Gọi
D
là chân đường cao kẻ từ
A
. Do
b c
nên
D
thuộc tia
MC
.
Áp dụng định lí Pythagore cho tam giác
ADB
, ta có
2 2 2 2 2 2 2 2
( ) 2AB BD AD BM MD AD BM BM MD MD AD
Suy ra
2 2 2
1
2AB BM BM MD AM
Một cách tương tự, áp dụng định lî Pythagore cho tam giác
ADC
, cũng được
2 2 2 2 2
)
2
( 2AC AD MC MD MC MC MD AM
Từ (1) và (2) suy ra
2 2 2 2 2 2 2 2
2( ) 2 2AB AC BM CM BM MD CM MD AM BM CM AM
hay
2 2 2
2
2 4
a
b c a
m
.
b) Từ công thức tinh diện tich tam giác suy ra
1 1 1 1 .
2 2 2
abc
p a b c
r S S S S h h h
Nhận xét
- Công thức
2 2 2
2
2 4
a
b c a
m
cho phép ta tính được độ dài đường trung tuyến của một tam giác, khi biết ba
cạnh của nó. Có thể thu được công thức này bằng cách làm như trong bài
3.16
(Toán 10, tập một).
- Nếu gọi
E
là điểm đối xứng với
A
qua
M
, thì tứ giác
ABEC
là một hình bình hành với hai đường chéo
,BC AE
. Khi đó công thức tính độ dài đường trung tuyến ở phần a) trở thành
2 2 2 2 2 2
BC AE AB BE EC CA
.
Ví dụ 4. Cho tam giác
ABC
có các góc thoả mãn
sin 2 sin cos C B A
. Chứng minh rằng tam giác
ABC
là một tam giác cân.
Giải
Áp dụng các định lí sin và côsin, ta có
2 2 2
2 2 2 2
sin 2 sin cos 2 cos 2 .
2
b c a
C B A c b A c b c b c a a b
bc
Vậy tam giác
ABC
cân tại
C
.
Ví dụ 5. Để đo chiều cao của một tòa nhà, người ta chọn hai điểm
A
và
B
thẳng hàng với chân
C
của tòa
nhà, cách nhau
15 m
. Sử dụng giác kế, từ
A
và
B
tương ứng nhìn thấy đỉnh
D
của tòa nhà dưới các góc
35
và
40
so với phương nằm ngang. Hỏi chiều cao của tòa nhà đo được là bao nhiêu mét?
Giải
Do
40 , 35
CBD BAD
nên
40 35 5
ADB
. Áp dụng định lí
sin
cho tam giác
ABD
ta được
15
sin sin35
sin sin5
AB
BD A
D
.
Từ đó suy ra chiều cao của tòa nhà bằng
15
sin sin 35 sin 40 63, 45( ).
sin 5
h CD BD CBD m