TOÁN 10-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG Điện thoại: 0946798489
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
PHẦN 1. LÝ THUYẾT – VÍ DỤ
CHƯƠNG 4. VECTƠ
Bài 7. CÁC KHÁI NIỆM MỞ ĐẦU
A - Kiến thức cần nhớ
1. Vectơ là một đoạn thẳng có hướng, nghĩa là, trong hai đầu mút của đoạn thẳng, đã chỉ rõ điềm đầu, điềm
cuối.
Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó. Đường thẳng đi qua điểm đầu và
điểm cuối của một vectơ được gọi là giá của vectơ đó.
2. Một vectơ hoàn toàn được xác định khi biết hướng và độ dài của nó.
3. Hai vectơ được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau.
Đối với hai vectơ cùng phương thì chúng cùng hướng hoặc ngược hướng.
4. Hai vectơ được gọi là bằng nhau nếu chúng có cung độ dài và cùng hướng.
5. Vectơ - không là vectơ có điểm đầu và điểm cuối trùng nhau.
Vectơ
0
có độ dài bằng 0 , cùng phương với mọi vectơ, cùng hướng với mọi vectơ.
B - Ví dụ
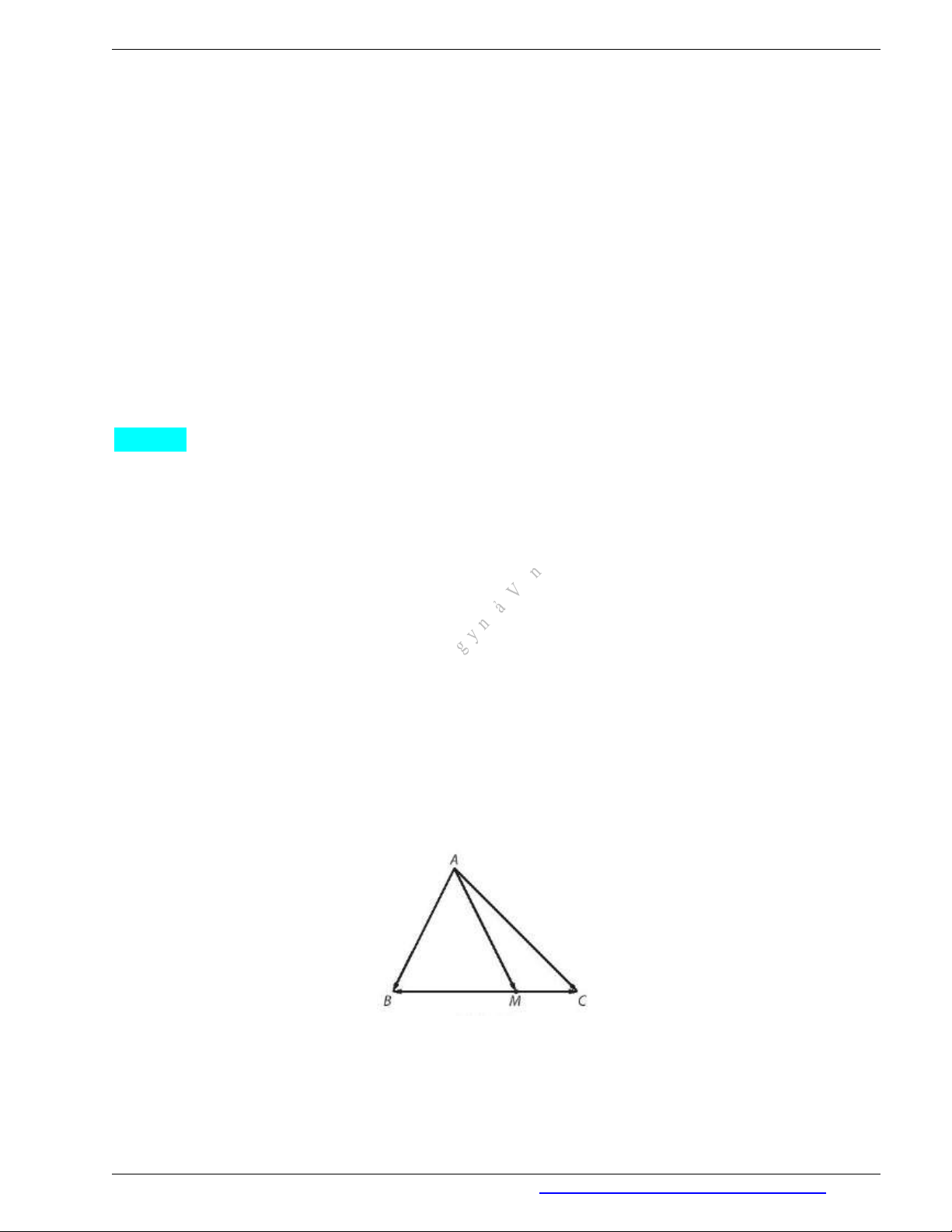
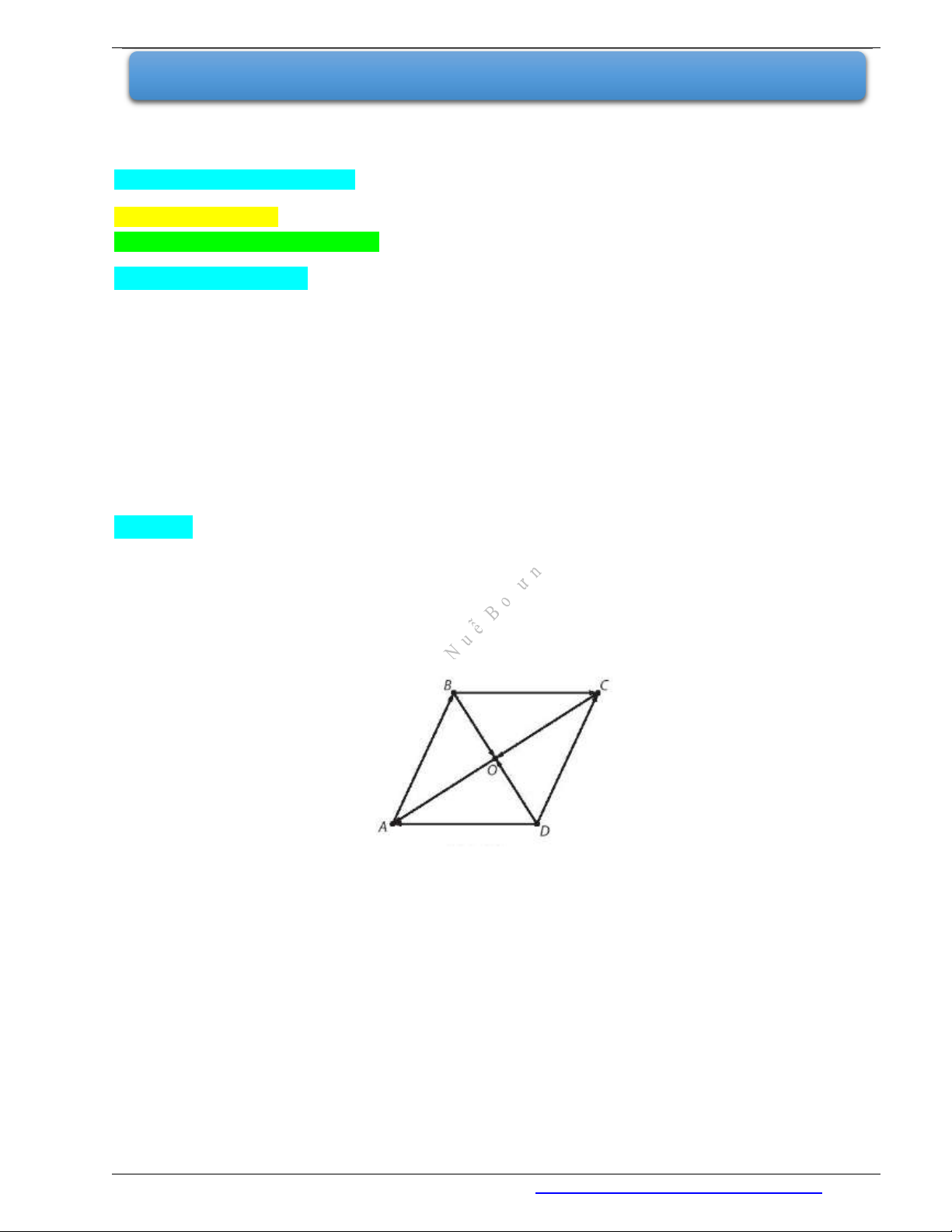
Ví dụ 1. Cho hình thoi
ABCD
. Gọi
O
là giao điểm của hai đường chéo
,AC BD
. Xét các cặp vectơ:
AB
và
,
DC DA
và
,
BC BC
và
,
CD OA
và
,
CO BO
và
DO
.
a) Hãy chỉ ra mối quan hệ về phương, hướng và độ dài của các vectơ trong mỗi cặp trên.
b) Trong các cặp trên, có bao nhiêu cặp gồm hai vectơ bằng nhau?
Giải
a) Do tứ giác
ABCD
là hình thoi, nên các cặp cạnh đối diện song song và bằng nhau, hai đường chéo cắt
nhau tại trung điểm của mỗi đường. Từ đó
- Hai vectơ
AB
và
DC
cùng hướng và cùng độ dài;
- Hai vectơ
DA
và
BC
ngược hướng và cùng độ dài;
- Hai vectơ
BC
và
CD
không cùng phương, nhưng có độ dài bằng nhau;
- Hai vectơ
OA
và
CO
cùng hướng và cùng độ dài;
- Hai vectơ
BO
và
DO
cùng độ dài, nhưng ngược hướng.
b) Theo kết quả của câu a,
- Do hai vectơ
AB
và
DC
cùng hướng và cùng độ dài, nên
AB DC
;
- Do hai vectơ
OA
và
CO
cùng hướng và cùng độ dài, nên
OA CO
;
- Do hai vectơ
DA
và
BC
có cùng độ dài, nhưng ngược hướng nên
DA
và
BC
không bằng nhau. Tương
tự,
BO
và
DO
không bằng nhau;
- Do hai vectơ
BC
và
CD
không cùng phương, vì vậy
BC
và
CD
không bằng nhau.
ÔN TẬP CHƯƠNG 4. VEC TO
•TOÁN 10
•|FanPage: Nguyễn Bảo Vương
Blog: Nguyễn Bảo Vương:
https://www.nbv.edu.vn/
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vậy, trong những cặp vectơ được xét, có 2 cặp gồm hai vectơ bằng nhau, đó là
AB
và
DC
;
OA
và
CO
.
Ví dụ 2. Cho tam giác
ABC
. Vẽ các đường trung tuyến
, ,AD BE CF
của tam giác
( , , ) D BC E CA F AB
. Xét các vectơ có đầu mút được lấy từ các điểm
,A B
, C, D, E, F.
Hãy chỉ ra các bộ ba vectơ khác
0
và đôi một bằng nhau.
Giải
Từ giả thiết suy ra
D
là trung điểm
,BC E
là trung điểm
CA
và
F
là trung điểm
AB
. Từ đó
, ,DE EF FD
là các đường trung bình của tam giác. Do đó, hai đoạn thẳng
,DE BF
song song và bằng nhau, hai đoạn
thằng
,DE FA
song song và bằng nhau. Suy ra các tứ giác
,AEDF FEDB
là hình bình hành. Do đó các
vectơ
, ,
BF DE FA
cùng hướng và cùng độ dài; các vectơ
, ,
AF FB ED
cùng hướng và cùng độ dài. Bởi vậy
BF FA DE
và
AF FB ED
.
Bằng lập luận tương tự, cũng được
vaø
vaø .
BD DC FE CD DB EF
CE EA DF AE EC FD
BÀI 8. TỔNG VÀ HIỆU CỦA HAI VECTƠ
A - Kiến thức cần nhớ
1. Vectơ đối
Vectơ đối của vectơ
a
, ki hiệu
a
, là vectơ ngược hướng và cùng độ dài với vectơ
a
.
2. Quy tắc cộng, trừ hai vectơ
- Quy tắc ba điểm (hay còn được gọi là quy tắc tam giác):
Với ba điểm bất kì
, ,A B C
, ta có:
; .AB BC AC AC AB BC
- Quy tắc hình bình hành: Nếu
ABCD
là hình bình hành thì
AB AD AC
.
3. Tính chất
- Tính chất giao hoán của phép cộng:
, ,
a b b a a b
.
- Tính chất kết hợp của phép cộng:
( ) ( ), , ,
a b c a b c a b c
.
- Tính chất của vectơ
0 : 0 0 ,
a a a a
.
- Tính chất của vectơ đối:
( ) 0,
a a a
.
4. Dấu hiệu nhận biết trung điểm đoạn thẳng, trọng tâm tam giác
M
là trung điểm đoạn thẳng
AB
khi và chỉ khi
0
MA MB
.
- G là trọng tâm tam giác
ABC
khi và chỉ khi
0
GA GB GC
.
B-Ví dụ
Ví dụ 1. Cho hình chữ nhật
ABCD
với
, 2 AB a AD a
.
a) Tính độ dài của vectơ
DC BD AB
.
b) Xác định điểm
M
sao cho
DC BD AB BM
.
Giải
Điện thoại: 0946798489 TOÁN 10-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
a) Do hình chữ nhật
ABCD
có
, 2 AB a AD a
nên độ dài hai đường chéo
,AC BD
bằng
2 2
( 2) 3 a a a
.
Theo tính chất giao hoán và kết hợp phép cộng vectơ, ta có
( ) .
DC BD AB AB BD DC
AB BD DC AD DC AC

Do đó
| | | | 3
 
DC BD AB AC a
.
b) Do
DC BD AB AC
nên
DC BD AB BM
AC BM
.
Theo kết quả bài tập 4.3, SGK Toán 10 tập 1 , đẳng thức
AC BM
tương đương với tứ giác
ABMC
là một
hình bình hành. Từ đó
CM AB DC
. Vậy điểm
M
cần tìm là điểm đối xứng với
D
qua
C
.
Ví dụ 2. Cho lục giác đều
ABCDEF
tâm
O
, độ dài các cạnh bằng 1 .
a) Chứng minh rằng
0. OA OB OC OD OE OF
b) Tính độ dài của các vectơ
,
AB OE AB CD EF
.
Giải
a) Do
O
là tâm của lục giác đều
ABCDEF
nên
O
là trung điềm của các đường chéo
, ,AD BE CF
.
Khi đó
0, 0, 0

OA OD OB OE OC OF
.
Suy ra
0
OA OB OC OD OE OF
.
b) Theo kết quả của bài tập 4.4, ta được
AB OE FO OE FE
Blog: Nguyễn Bảo Vương:
https://www.nbv.edu.vn/
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Từ đó, do độ dài các cạnh của lục giác
ABCDEF
bằng 1 nên
| | | | 1
AB OE EF
.
Ví dụ 3. Trên Hình biểu diên ba lực
1
F
,
2 3
,
F F
cùng tác động vào một vật ở vị trí cân bằng 0 . Cho biết
cường độ của
1 2
,
F F
đều bằng
100 N
và góc tạo bởi
1
F
và
2
F
bằng
120
.
Tính cường độ của lực
3
F
.
Giải
Ta sử dụng các vectơ
, ,

OA OB OC
và
OD
lần lượt biểu diễn cho các lực
1 2 3
, ,
F F F
và hợp lực
F
của
1 2
,
F F
.
Khi đó, do
1 2
FFF
và
1 2
100
F F
, nên tứ giác
AOBD
là hình thoi. Từ đó, do
120
AOB
, suy ra
60
OAD
, do đó tam giác
AOD
đều. Bởi vậy
| | 100
F OD OA
.
Do vật ở vị trí cân bằng nên hai lực
F
và
3
F
ngược hướng và có cường độ bằng nhau, tức là hai vectơ
OD
và
OC
là hai vectơ đối nhau. Suy ra cường độ của lực
3
F
bằng
3
| | 100( ). F F N
BÀI 9. TÍCH CỦA MỘT VECTƠ VỚI MỘT SỐ
A - Kiến thức cần nhớ
1. Tích của vectơ
0
a
với số thực
k
, kí hiệu
ka
, là một vectơ:
- có độ dài bằng
| | | |
k a
;
Điện thoại: 0946798489 TOÁN 10-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
- cùng hướng với
a
khi
0k
và ngược hướng với
a
khi
0k
;
2. Tính chất. Cho hai vectơ
,
a b
và cho hai số thực
k
, t. Khi đó
( ) ( )
k ta kt a
;
( ) ; ( ) ;
k a b ka kb k a b ka kb
( )
k t a ka ta
-
1 ,( 1) ;
a a a a
0 0
ka k
hoặc
0
a
.
3. Hai vectơ
a
và
( 0)
b b
cùng phương khi và chỉ khi tồn tại số thực
k
sao cho
a kb
4. Cho trước vectơ
0
a
. Khi đó với mọi vectơ
b
cùng phương với
a
, tồn tại duy nhất số thực
x
sao cho
b xa
.
5. Cho trước hai vectơ
a
và
b
không cùng phương. Khi đó với mọi vectơ
c
tồn tại duy nhất cặp số
( ; )x y
sao cho
.
6.
M
là trung điểm của
AB
khi và chỉ khi
2 ,
OA OB OM O
.
G
là trọng tâm tam giác
ABC
khi và chỉ
khi
3 ,
OA OB OC OG O
.
B. Ví dụ
Ví dụ 1. Cho tam giác
ABC
. Gọi
M
là trung điểm của
BC
. Gọi
1 2
, ,G G G
theo thứ tự là trọng tâm các tam
giác
, ,ABC ABM ACM
. Chứng minh rằng
G
là trung điềm của
1 2
G G
.
Giải
Do
M
là trung điểm của
1 2
; , ,BC G G G
theo thứ tự là trọng tâm các tam giác
, ,ABC ABM ACM
nên với
mọi điềm
O
, ta có
1 2
2 , 3
3 , 3 .
OB OC OM OA OB OC OG
OA OB OM OG OA OC OM OG
Tử đó suy ra
1 2
3 ( ) ( 2 )
( ) ( ) 6
OG OG OA OB OC OA OM
OA OB OC OA OB OC OG

Suy ra
1 2
2
OG OG OG
. Do đó
G
là trung điểm của
1 2
G G
.
Ví dụ 2. Cho tam giác
ABC
. Trên cạnh
BC
lấy điểm
M
sao cho
2BM MC
.
a) Chứng minh rằng
2 0
MB MC
.
b) Chứng minh rằng
2 3
AB AC AM
.
Giải
a) Do
M
thuộc cạnh
BC
và
2BM MC
nên hai vectơ
,
MB MC
ngược hướng và
| | 2 | |
MB MC
. Suy ra
2
MB MC
và do đó
2 0
MB MC
.
b) Theo quy tắc ba điểm, ta có
;

AB AM MB AC AM MC
.
Từ đó
2 ( ) 2( ) 3 ( 2 ) 3
     
AB AC AM MB AM MC AM MB MC AM
.
Nhận xét
- Điểm
M
trong ví dụ này được gọi là điểm chia đoạn thẳng
BC
theo tỉ số
2
.