Nguyễn Vũ Minh minhnguyen249@yahoo.com Lượng Giác
0914449230 1
Lượng Giác
αααααααα
A. HÀM SỐ LƯỢNG GIÁC VÀ CÁC VẤN ĐỀ CÓ LIÊN QUAN :
1) Hàm số lượng giác :
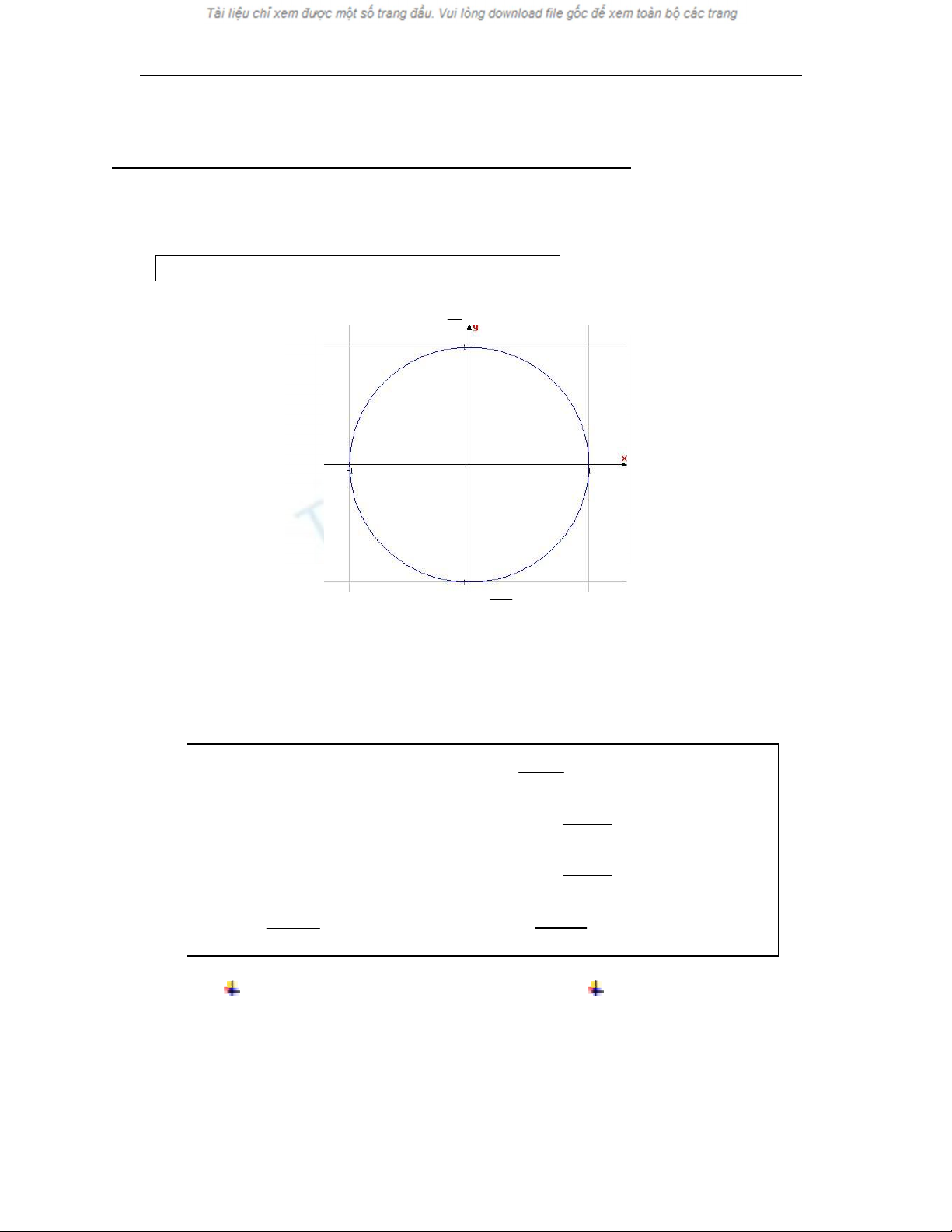
Vòng tròn lượng giác : Vòng tròn tâm ,bán kính R = 1 ,chiều dương ngược chiều
kim đồng hồ ( trong hệ trục Oxy )
4 hàm số lượng giác : y = sinx ( Oy ) , y = cosx ( Ox ) , y = tanx , y = cotx
1 sin ,cos 1
và
tan ,cot
 
2) Tính tuần hoàn :
Sin (x + k.2
) = sinx
Cos (x + k.2
) = cosx Tan (x + k.
) = tanx
Cot (x+k.
) = cotx
Hàm six ,cosx tuần hoàn với chu kì 2
, hàm tanx ,cotx tuần hoàn với chu kì
3) Hệ thức cơ bản :
2 2
;
sin
tan
cos
;
cos
cot
sin
tan .cot 1
1
cot
tan
1
tan
cot
2
2
1
1 tan
cos
; 2
2
1
1 cot
sin
4) Dấu của các giá trị Lượng Giác :
Trong cung phần tư
thứ (1) :
sin 0
cos 0
tan 0
cot 0
x
x
x
x
Trong cung phần tư
thứ (2) :
sin 0
cos 0
tan 0
cot 0
x
x
x
x
O
(1)
(4) (3)
(2)
2
0
3
2
2
Nguyễn Vũ Minh minhnguyen249@yahoo.com Lượng Giác
0914449230 2
Trong cung phần tư
thứ (3) :
sin 0
cos 0
tan 0
cot 0
x
x
x
x
Trong cung phần tư
thứ (3) :
sin 0
cos 0
tan 0
cot 0
x
x
x
x
5) Các cung liên kết :
Hai cung đối nhau :
&
x x
cos( ) cos
sin( ) sin
tan( ) tan
cot( ) cot
x x
x x
x x
x x
Hai cung bù nhau : &
x x
sin( ) sin
cos( ) cos
tan( ) tan
cot( ) cot
x x
x x
x x
x x
Hai cung phụ nhau : &
2
x x
sin cos
2
cos sin
2
tan cot
2
cot tan
2
x x
x x
x x
x x
Hai cung hơn
2
: &
2
x x
sin cos
2
cos sin
2
tan cot
2
cot tan
2
x x
x x
x x
x x
Chú ý : Đối với sin và cos : chẵn
bỏ ; lẻ
bỏ ,thêm dấu
ở
trước
Nguyễn Vũ Minh minhnguyen249@yahoo.com Lượng Giác
0914449230 3
Đối với tan và cot : chẵn hay lẻ
ta bỏ vô tư ko cần thêm gì nữa
B. CÔNG THỨC LƯỢNG GIÁC :
CÔNG THỨC CỘNG :
sin( ) sin .cos cos .sin
cos( ) cos .cos sin .sin
tan tan
tan( ) 1 tan .tan
a b a b a b
a b a b a b
a b
a b a b
HỆ QUẢ :
sin cos 2sin
4
cos sin 2 cos
4
a a a
a a a
CÔNG THỨC NHÂN :
Nhân đôi :
2 2 2 2
2
sin 2 2sin .cos
cos2 cos sin 2cos 1 1 2sin
2tan
tan 2 1 tan
x x x
x x x x x
x
xx
Nhân ba :
3
sin3 3sin 4sin
x x x
; 3
cos3 4cos 3cos
x x x
Tổng thành Tích :
cos cos 2cos .cos
2 2
cos cos 2sin .sin
2 2
sin sin 2sin .cos
2 2
sin sin 2cos .sin
2 2
a b a b
a b
a b a b
a b
a b a b
a b
a b a b
a b
nhận xét :
2
a b
đứng trước,
2
a b
đứng sau
Tích Thành Tổng :
1
cos .cos [cos( ) cos( )]
21
sin .sin [cos( ) cos( )]
2
1
sin .cos [sin( ) sin( )]
2
1
cos .sin [sin( ) sin( )]
2
CÔNG THỨC HẠ BẬC :
2
1 cos2
sin
2
x
x
; 2
1 cos2
cos
2
x
x
C. PHƯƠNG TRÌNH LƯỢNG GIÁC :
Phương trình Lượng Giác cơ bản :
2
sin sin ( )
2
u v k
u v k Z
u v k
cos cos 2 ,( )
u v u v k k Z
Nguyễn Vũ Minh minhnguyen249@yahoo.com Lượng Giác
0914449230 4
tan tan
;( )
cot cot
u v
u v k k Z
u v
Chú ý : khi giải ta cần qui về cơ bản nếu ko gặp dạng này
khi gặp phương trình dạng :
cos cos
u v
đưa về
cos cos( )
u v
;
sin sin
u v
đưa về
sin sin( )
u v
tan tan
u v
đưa về
tan tan( )
u v
;
cot cot
u v
đưa về
cot cot( )
u v
Phương trình bậc 2 ( hoặc cao hơn ) đối với hàm số LG :
Dạng :
2
2
2
2
.sin .sin 0
.cos .cos 0
.tan .tan 0
.cot .cot 0
a x b x c
a x b x c
a x b x c
a x b x c
, Cách giải : đặt
sin ,( 1 1)
cos ,( 1 1)
tan ,( )
cot ,( )
t x t
t x t
t x t R
t x t R
Pt cho sẽ trở thành : 2
. . 0
a t b t c
t x
Phương trình đối xứng với sinx và cosx :
.sin cos
a u b u c
; đk có nghiệm :
2 2 2
a b c
Cách giải : chia 2 vế phương trình cho
2 2
a b
Phương trình cho trở thành :
2 2 2 2 2 2
.sin cos
a b c
u u
a b a b a b
Đặt 2 2 2 2
cos sin
a b
a b a b
, bằng tư duy ta đưa về công
thức :
sin( ) sin .cos cos .sin
cos( ) cos .cos sin .sin
a b a b a b
a b a b a b
sau đó giải bình thường
tức là
2 2 2 2
sin .cos cos .sin sin( )
c c
u u u
a b a b
Nguyễn Vũ Minh minhnguyen249@yahoo.com Lượng Giác
0914449230 5
Phương trình đẳng cấp đối với sinx & cosx :
2 2
.sin .sin .cos .cos
a u b u u c u d
(1)
Cần nhớ : 2
2
sin2 2sin .cos
11 tan
cos
u u u
u
u
Cách giải1 :
o Xét 2
cos 0 sin 1
x x
, nếu VT = VP thì cosx = 0 là 1 nghiệm
của pt, nếu ko thỏa thì cosx = 0 ko fải là nghiệm
o Xét
cos 0
x
, chia 2 vế phương trình (1) cho 2
cos
x
và nhớ
2
2
.(1 tan )
cos
d
d x
x
hay 2 2
(sin cos )
d d x x
, sau đó đưa về
phương trình bậc 2 theo tanx và giải
Cách giải2 :
1 cos2 sin 2 1 cos2
. . .
2 2 2
x x x
a b c d
.sin 2 cos2
A x B x C
( đã học ,
dùng trong biện luận nghiệm nhiều hơn )
Phương trình chứa tổng và tích :
.(sin cos ) sin .cos 0
a u u b u u c
Cách giải : đặt
sin cos 2sin( )
4
t u u u
,đk
2 2
t sau đó bình
phương và rút
sin .cos
u u
theo t và thế vào pt giải bình thường sẽ có nghiệm t
Phương trình quy về dạng tích :
0
. . 0 0
0
A
A B C B
C
Phương trình tổng bình phương :
2 2
0
0
0
A
A B B