TIẾT 92
BÀI TẬP ÔN CUỐI NĂM
A. PHẦN CHUẨN BỊ.
I. Yêu cầu bài dạy.
1. Yêu cầu về kiến thức, kỹ năng, tư duy.
- Hệ thống lại ứng dụng của đại hàm vào việc tìm giá trị lớn nhất, giá trị nhỏ nhất
, khoảng lồi, lõm và điểm uốn của đồ thị hàm số và phương pháp giải bài tập này.
- Rèn luyện kỹ năng nhớ, tính toán, tính nhẩm, phát triển tư duy cho học sinh.
Rèn luyện tính cẩn thận, chính xác, khoa học cho học sinh.
2. Yêu cầu về giáo dục tư tưởng tình cảm.
- Qua bài giảng, học sinh say mê bộ môn hơn và có hứng thú tìm tòi, giải quyết
các vấn đề khoa học.
II. Phần chuẩn bị.
1. Phần thày: SGK, TLHDGD, GA.
2. Phần trò: Vở, nháp, SGK, chuẩn bị trước nội dung bài ở nhà.
B. PHẦN THỂ HIỆN TRÊN LỚP.
I. Kiểm tra bài cũ ( 6’ )
1. Câu hỏi: Nêu quy tắc tìm cự trị của HS theo dấu hiệu II ?. áp dụng tìm cự trị của
hàm số y = x4 – 4x3 + 4x2.
2. Đáp án: - Quy tắc ( SGK )
- áP dụng: TXĐ: D = R; y’ = 4x3 - 12x2 + 8x = 4x(x2 – 3x + 2)
y’ = 0 <=> x = 0 hoặc x = 1 hoặc x = 2.
y” = 12x2 – 24x + 8.
Ta có y”(0) = 8 > 0 => HS đạt cự tiểu tại x = 0 và yCT = 0.
y”(1) = -4 < 0 => HS đạt cự đại tại x = 1 và yCĐ = 1.
y”(2) = 8 => HS đạt cự tiểu tại x = 2 và yCT = 0.
II. Bài mới.
1. Đặt vấn đề: Trong tiết trước chúng ta đã đi củng cố lại phần ứng dụng của đạo
hàm vào tìm khoảng đơn điệu và cự trị của hàm số, nay ta đi củng cố lại phần tìm
giá trị lớn nhất, giá trị nhỏ nhất của hàm số.
2. Bài mới:
PHƯƠNG PHÁP T/
G NỘI DUNG
- Nêu cách tìm giá trị lớn nhất, giá
trị nhỏ nhất của hàm số / (a;b) ?
8’
Phần: GIÁ TRỊ LỚN NHẤT, GIÁ TRỊ
NHỎ NHẤT
A. Lý thuyết.
1/. Tìm giá trị lớn nhất, giá trị nhỏ nhất
của hàm số trên khoảng.
2/. Tìm giá trị lớn nhất, giá trị nhỏ nhất
- Nêu cách tìm giá trị lớn nhất, giá
trị nhỏ nhất của hàm số / [a;b] ?
- áp dụng quy tắc tìm gí trị lớn
nhất, nhỏ nhất của hàm số / [a;b]
vào hàm số này?.
- GV gọi HS len thực hiện tương
tự.
18
’
của hàm số trên đoạn.
B. Bài tập.
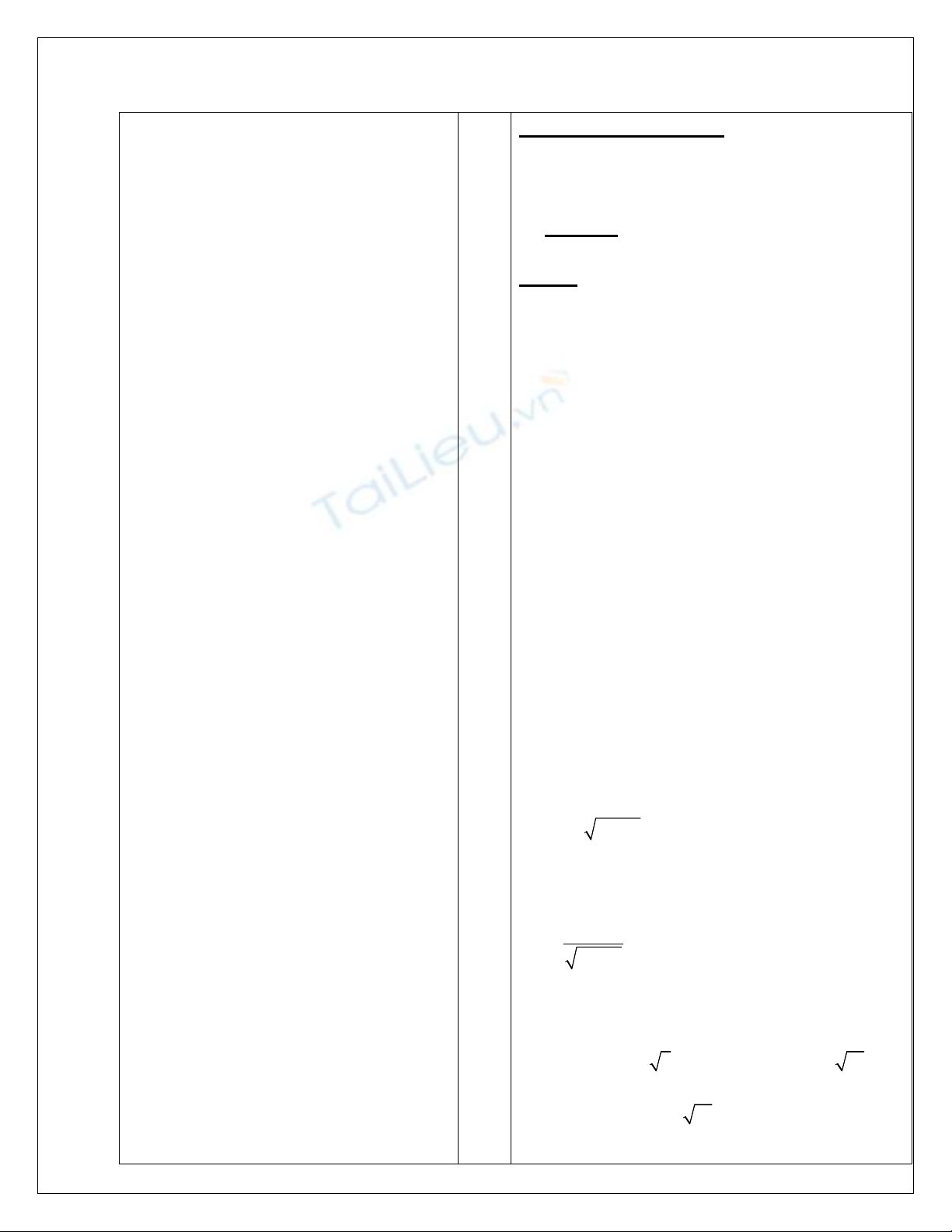
Bài 1: Tìm giá trị lớn nhất, nhỏ nhất của
các HS ?
a/. y = x.ex-1 trên [-2; 2]
TXĐ: D = R nên HS cũng XĐ/ [-2; 2]
y’ = ex-1 + x.ex-1 = ex-1.( x+ 1) XĐ/ D
y’ = 0 <=> x= -1
y(-2) = -2.e-3 = - 2/e3
y(-1) = -e-2 = -1/e2
y(2) = 2e
=> GTLN/[-2; 2] là yMax = y(2) = 2e
=> GTNN/ [-2; 2] là ymin = y(-1) = e-2
b/. y = 2
4
x
trên [-1; 3]
TXĐ: D = R nên HS cũng XĐ/ [-1; 3]
y’ = 2
4
x
x
XĐ/ D.
y’ = 0 <=> x = 0.
Ta có: y(-1) =
5
; y(0) = 2; y(3) =
13
Vậy yMax = y(3) =
13
; ymin = y(0) = 2.
- GV gọi HS đứng tại chỗ thực hiện
tương tự .
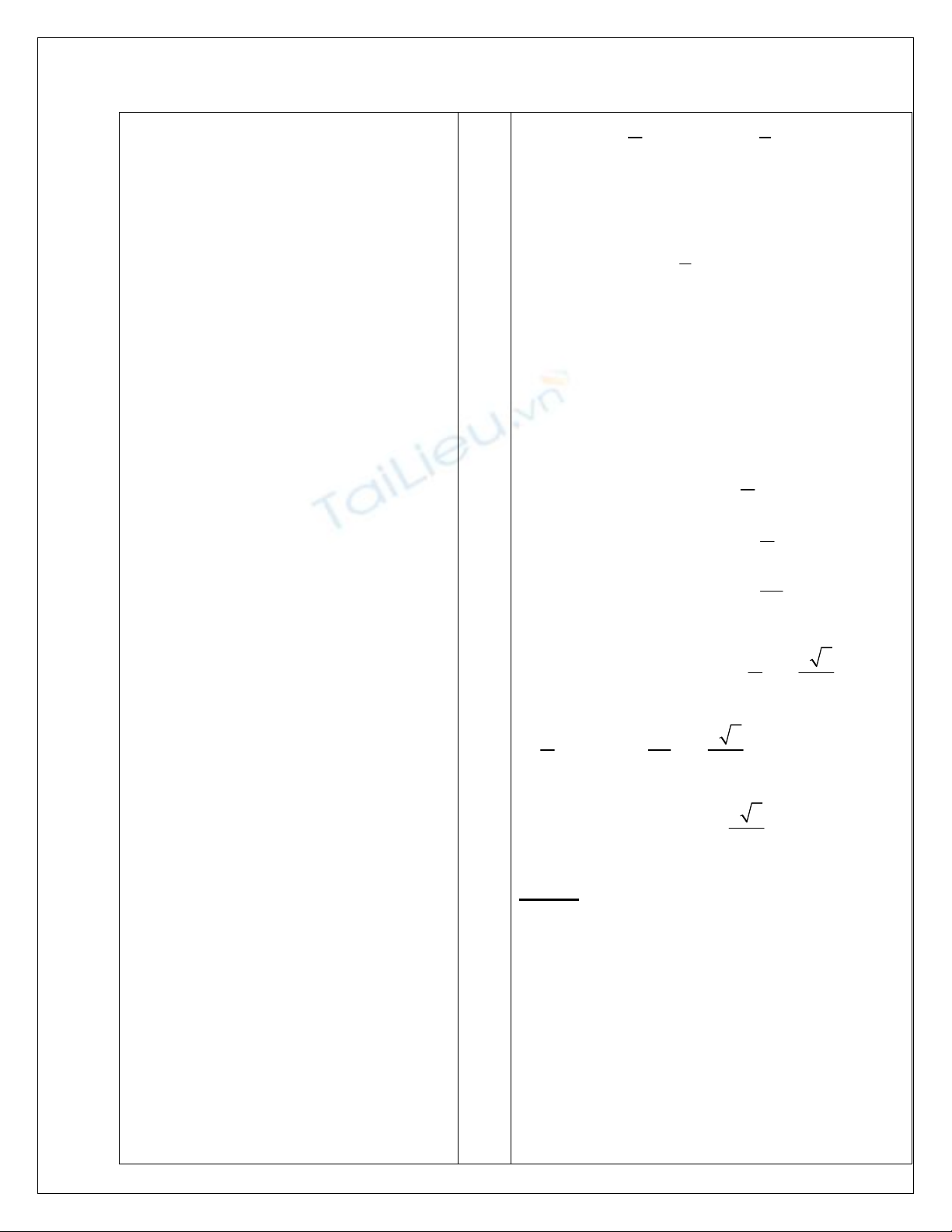
c/. y = Cos(
2
-x) + Sinx -
4
3
Sin3x trên [0;
]
Ta có y = 2Sinx -
4
3
Sin3x.
TXĐ: D = R nên HS cũng XĐ/ [0;
]
y’ = 2Cosx – 4.Sin2x.Cosx
= 2Cosx.(1-Sin2x) = 2Cosx.Cos2x XĐ/ D
y’ = <=>
02
4
2 0 3
4
Cosx x R
Cos x
Ta có: y(0) = y(
) = 0; y(
4
) =
2 2
3
y(
2
) = 2/3; y(
3
4
) =
2 2
3
Vậy trên [0;
]: yMax =
2 2
3
, ymin = 0.
Bài 2: Nhà máy cá hộp sản xuất những
hình trụ tròn xoay đựng cá ( hai đầu đều
kín ) với thể tích V(cm3) không đổi và
muốn tốc ít vật liệu làm vỏ nhất thì các
kích thước phải như thế nào ?
- Xác định diện tích nguyên liệu
làm lên phần diện tích hình hộp.
Phần diện tích đó phụ thuộc vào
đâu?
=> Cách giải ?
- Xác định dạng bài toán và
phương pháp giải ?
10
’
Giải:
Muốn tốn ít vật liệu nhất thì diện tích toàn
phần của hình trụ phải nhỏ nhất.
- Gọi chiều cao của hình trụ là x cm ( x >
0 )
Bán kính đáy là y cm ( y > 0 )
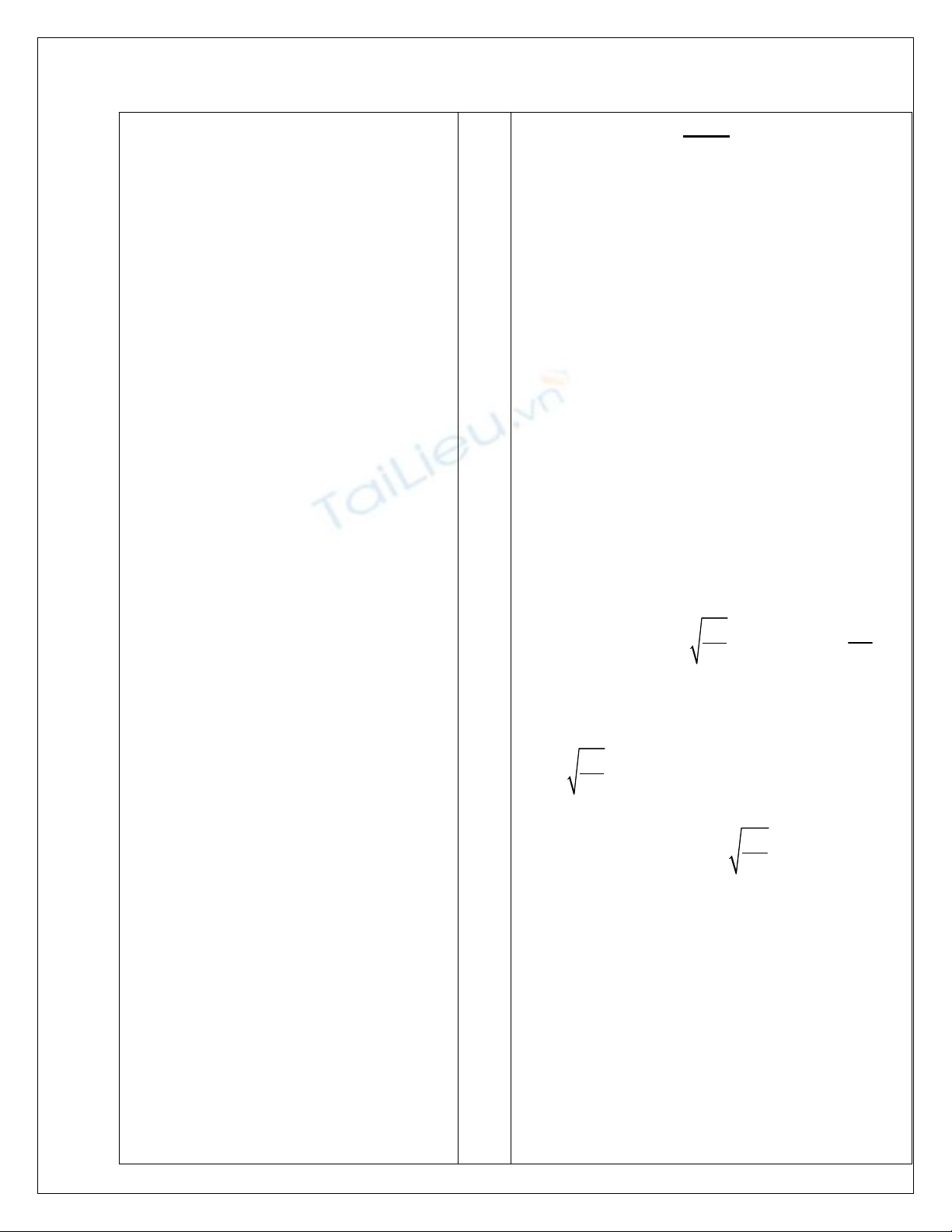
Ta có Stp = 2
yx + 2
y2
Mà V =
y2x => x = V/(
y2)
Nên Stp = 2V/y + 2
y2
=> Stp’ = -2V/(y2) + 4
y.
Stp’ = 0 <=> y = 3
2
V
=> Stp” =
3
4
V
y
+
4
Stp”( 3
2
V
) = 12
> 0
=> Stp nhỏ nhất khi y = 3
2
V
=> x = 2y
Vậy muốn tốn ít nguyên liệu nhất thì hộp
phải có đường kính đáy bằng đường cao.