
Nguyen DInh Phuong
Bài 12 M ngả
M c tiêu:ụ
K t thúc bài h c này, b n có th :ế ọ ạ ể
S d ng m ng m t chi uử ụ ả ộ ề
S d ng m ng hai chi u.ử ụ ả ề
Các b c trong bài h c này đ c trình bày chi ti t, rõ ràng và c n th n. Đi u này giúp ta hi u rõ vướ ọ ượ ế ẩ ậ ề ể ề
công c l p trình. Th c hi n theo các b c sau th t c n th n.ụ ậ ự ệ ướ ậ ẩ ậ
Ph n I – Trong th i gian 1 gi 30 phút đ u:ầ ờ ờ ầ
12.1 M ngả
Các m ng có th đ c phân làm hai d ng d a vào chi u c a m ng: M ng m t chi u và m ng đaả ể ượ ạ ự ề ủ ả ả ộ ề ả
chi u. Trong bài này, chúng ta s t p trung vào cách t o và s d ng các m ng.ề ẽ ậ ạ ử ụ ả
12.1.1 S s p x p m t m ng m t chi uự ắ ế ộ ả ộ ề
M ng m t chi u có th đ c s d ng đ l u tr m t t p các giá tr có cùng ki u d li u. Xét m tả ộ ề ể ượ ử ụ ể ư ữ ộ ậ ị ể ữ ệ ộ
t p đi m c a sinh viên trong m t môn h c. Chúng ta s s p x p các đi m này theo th t gi mậ ể ủ ộ ọ ẽ ắ ế ể ứ ự ả
d n. ầ
Các b c s p x p m ng m t chi u theo th t gi m nh sau:ướ ắ ế ả ộ ề ứ ự ả ư
1. Nh p vào s l ng các đi m. ậ ố ượ ể
Đ th c hi n đi u này, m t bi n ph i đ c khai báo và giá tr c a bi n ph i đ c nh p. Mã l nhể ự ệ ề ộ ế ả ượ ị ủ ế ả ượ ậ ệ
nh sau:ư
int n;
printf(“\n Enter the total number of marks to be entered : ”);
scanf(“%d”, &n);
2. Nh p vào t p các đi m. ậ ậ ể
Đ nh p vào t p các giá tr cho m t m ng, m ng ph i đ c khai báo. Mã l nh nh sau,ể ậ ậ ị ộ ả ả ả ượ ệ ư
int num[100];
S ph n t c a m ng đ c xác đ nh b ng giá tr đã nh p vào bi n n. n ph n t c a m ng ph iố ầ ử ủ ả ượ ị ằ ị ậ ế ầ ử ủ ả ả
đ c kh i t o giá tr . Đ nh p n giá tr , s d ng vòng l p ượ ở ạ ị ể ậ ị ử ụ ặ for. M t bi n nguyên c n đ c khai báoộ ế ầ ượ
đ s d ng nh là ch s c a m ng. Bi n này giúp truy xu t t ng ph n t c a m ng. Sau đó giá trể ử ụ ư ỉ ố ủ ả ế ấ ừ ầ ử ủ ả ị
c a các ph n t m ng đ c kh i t o b ng cách nh n các giá tr nh p vào t ng i dùng. Mã l nhủ ầ ử ả ượ ở ạ ằ ậ ị ậ ừ ườ ệ
nh sau:ư
int l;
for(l = 0; l < n; l++)
{
printf(“\n Enter the marks of student %d : ”, l + 1);
scanf(“%d”, &num[l]);
M ngả169
King.P
}
Vì các ch s c a m ng luôn b t đ u t 0 nên chúng ta c n kh i t o bi n ỉ ố ủ ả ắ ầ ừ ầ ở ạ ế l là 0. M i khi vòng l pỗ ặ
đ c th c thi, m t giá tr nguyên đ c gán đ n m t ph n t c a m ng.ượ ự ộ ị ượ ế ộ ầ ử ủ ả
3. T o m t b n sao c a m ng.ạ ộ ả ủ ả
Tr c khi s p x p m ng, t t h n là nên gi l i m ng g c. Vì v y m t m ng khác đ c khai báoướ ắ ế ả ố ơ ữ ạ ả ố ậ ộ ả ượ
và các ph n t c a m ng th nh t có th đ c sao chép vào m ng m i này. Các dòng mã l nh sauầ ử ủ ả ứ ấ ể ượ ả ớ ệ
đ c s d ng đ th c hi n đi u này:ượ ử ụ ể ự ệ ề
int desnum[100], k;
for(k = 0; k < n; k++)
desnum[k] = num[k];
4. S p x p m ng theo th t gi m d n. ắ ế ả ứ ự ả ầ
Đ s p x p m t m ng, các ph n t trong m ng c n ph i đ c so sánh v i nh ng ph n t còn l i.ể ắ ế ộ ả ầ ử ả ầ ả ượ ớ ữ ầ ử ạ
Cách t t nh t đ s p x p m t m ng, theo th t gi m d n, là ch n ra giá tr l n nh t trong m ngố ấ ể ắ ế ộ ả ứ ự ả ầ ọ ị ớ ấ ả
và hoán v nó v i ph n t đ u tiên. M t khi đi u này đ c th c hi n xong, giá tr l n th hai trongị ớ ầ ử ầ ộ ề ượ ự ệ ị ớ ứ
m ng có th đ c hoán v v i ph n t th hai c a m ng, ph n t đ u tiên c a m ng đ c b quaả ể ượ ị ớ ầ ử ứ ủ ả ầ ử ầ ủ ả ượ ỏ
vì nó đã là ph n t l n nh t. T ng t , các ph n t c a m ng đ c lo i ra tu n t đ n khi ph nầ ử ớ ấ ươ ự ầ ử ủ ả ượ ạ ầ ự ế ầ
t l n th n đ c tìm th y. Trong tr ng h p m ng c n s p x p theo th t tăng d n giá tr l nử ớ ứ ượ ấ ườ ợ ả ầ ắ ế ứ ự ầ ị ớ
nh t s đ c hoán v v i ph n t cu i cùng c a m ng.ấ ẽ ượ ị ớ ầ ử ố ủ ả
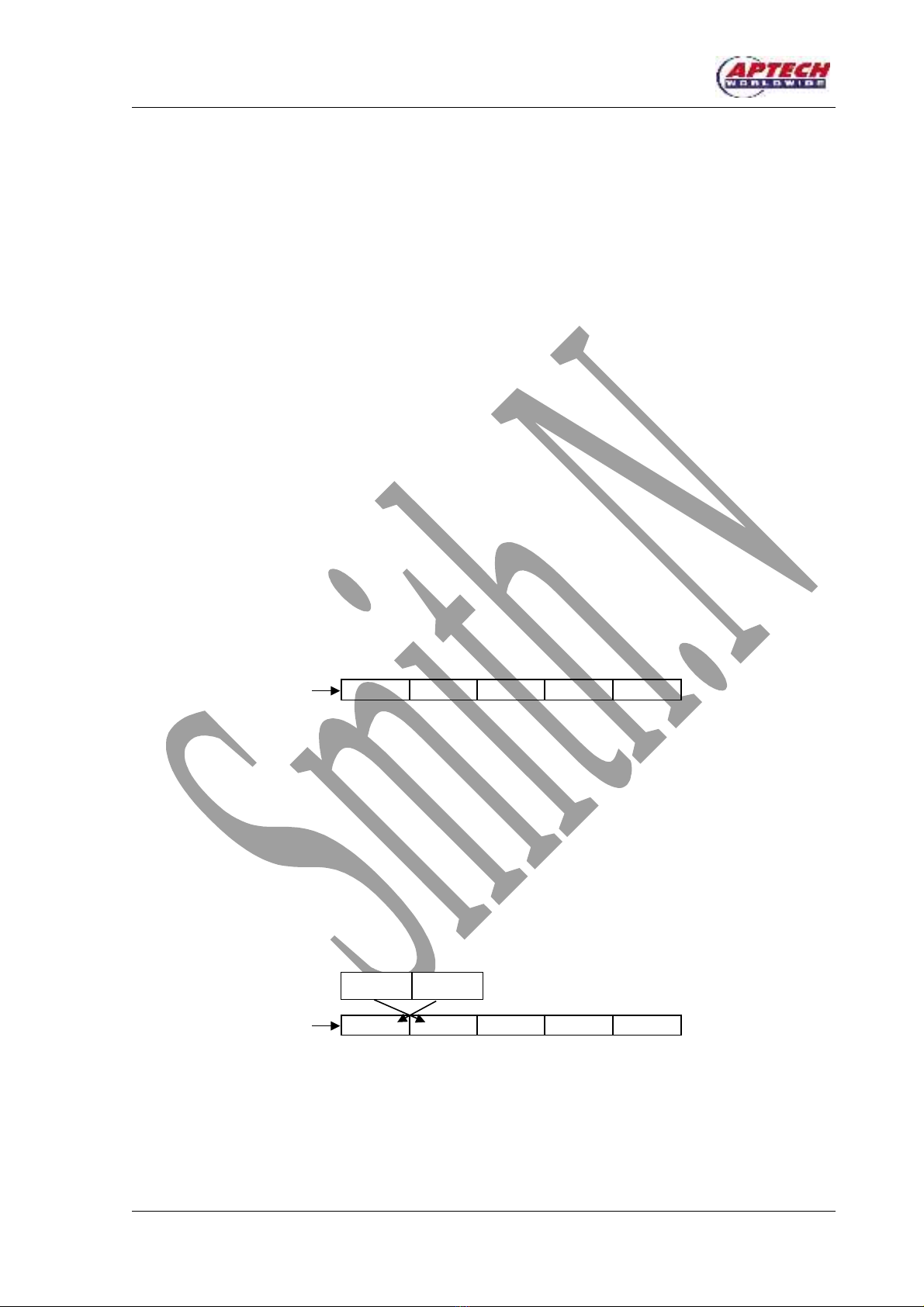
Quan sát ví d m t dãy s đ hi u đ c gi i thu t. Hình 12.1 trình bày m t m ng s nguyên c nụ ộ ố ể ể ượ ả ậ ộ ả ố ầ
đ c s p x p.ượ ắ ế
10 40 90 60 70
Hình 12.1: M ng num v i ch s i (5 ph n t )ả ớ ỉ ố ầ ử
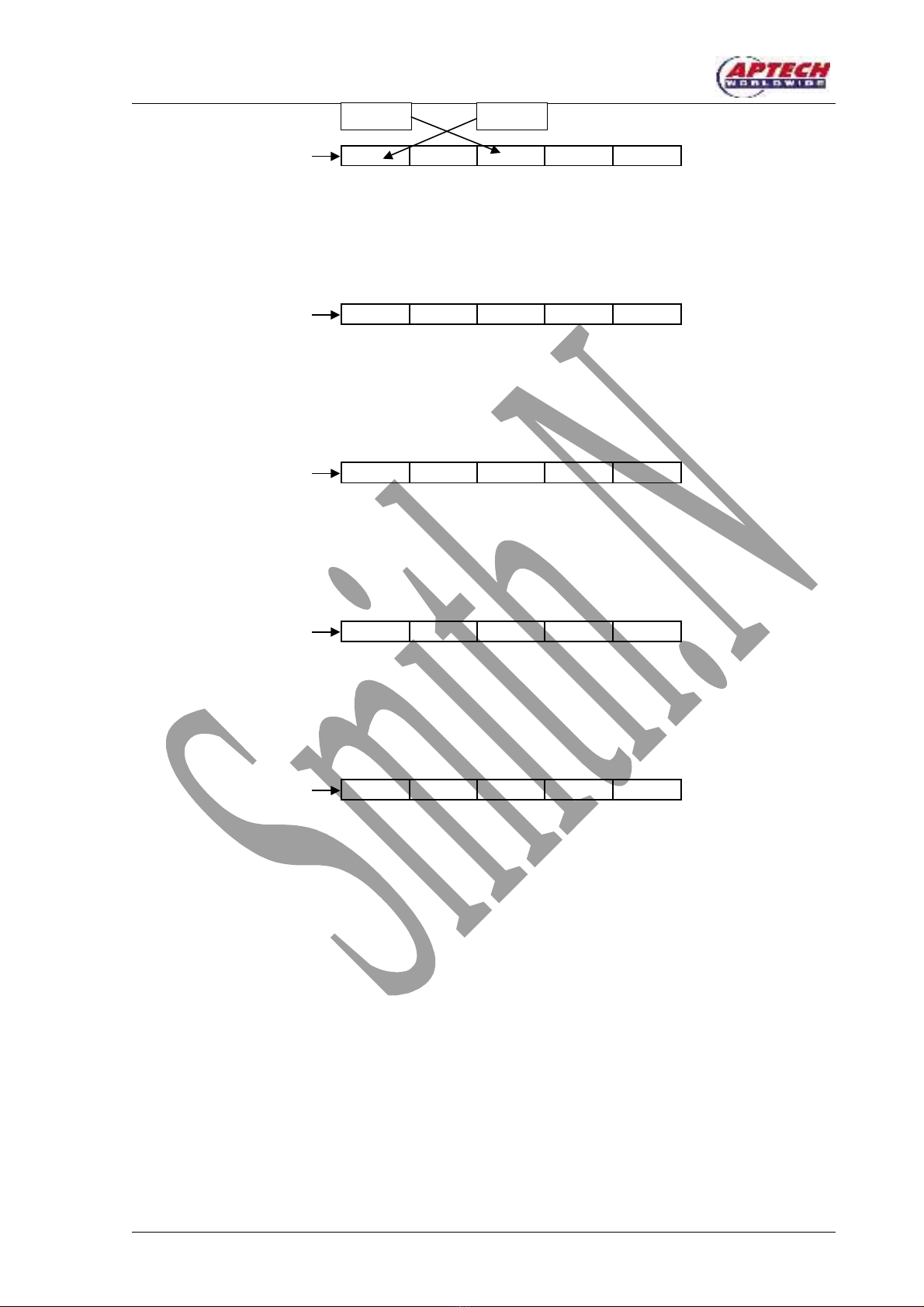
Đ s p x p m ng này theo th t gi m d n,ể ắ ế ả ứ ự ả ầ
a. Chúng ta c n tìm ph n t l n nh t và hoán v nó vào v trí ph n t đ u tiên. Xem nh đây làầ ầ ử ớ ấ ị ị ầ ử ầ ư
l n th c hi n th nh t. Đ đ a giá tr l n nh t v v trí đ u tiên, chúng ta c n so sánh ph n t thầ ự ệ ứ ấ ể ư ị ớ ấ ề ị ầ ầ ầ ử ứ
nh t v i các ph n t còn l i. Khi ph n t đang đ c so sánh l n h n ph n t đ u tiên thì hai ph nấ ớ ầ ử ạ ầ ử ượ ớ ơ ầ ử ầ ầ
t này c n ph i đ c hoán v . ử ầ ả ượ ị
Kh i đ u, l n th c hi n đ u tiên, ph n t ví trí th nh t đ c so sánh v i ph n t v trí thở ầ ở ầ ự ệ ầ ầ ử ở ứ ấ ượ ớ ầ ử ở ị ứ
hai. Hình 12.2 bi u di n s hoán v t i v trí th nh t.ể ễ ự ị ạ ị ứ ấ
40 10 90 60 70
Hình 12.2: Đ o v trí ph n t th nh t v i ph n t th haiả ị ầ ử ứ ấ ớ ầ ử ứ
Ti p đó, ph n t th nh t đ c so sánh v i ph n t th ba. Hình 12.3 bi u di n s hoán v gi aế ầ ử ứ ấ ượ ớ ầ ử ứ ể ễ ự ị ữ
ph n t th nh t và ph n t th ba.ầ ử ứ ấ ầ ử ứ
170 L p trình c b n Cậ ơ ả
num
i=0 i=4
i=0 i=4
num
10
40
Nguyen DInh Phuong
90 10 40 60 70
Hình 12.3 Đ o v trí ph n t th nh t v i ph n t th baả ị ầ ử ứ ấ ớ ầ ử ứ
Quá trình này đ c l p l i cho đ n khi ph n t th nh t đ c so sánh v i ph n t cu i cùng c aượ ặ ạ ế ầ ử ứ ấ ượ ớ ầ ử ố ủ
m ng. M ng k t qu sau l n th c hi n đ u tiên đ c trình bày trong hình 12.4 bên d i.ả ả ế ả ầ ự ệ ầ ượ ướ
90 40 10 60 70
Hình 12.4: M ng sau l n th c hi n đ u tiênả ầ ự ệ ầ
b. B qua ph n t đ u tiên, chúng ta c n tìm ph n t l n th hai và hoán v nó v i ph n t thỏ ầ ử ầ ầ ầ ử ớ ứ ị ớ ầ ử ứ
hai c a m ng. Hình 12.5 bi u di n m ng sau khi đ c th c hi n l n hai.ủ ả ể ễ ả ượ ự ệ ầ
90 70 10 60 40
Hình 12.5: M ng sau l n th c hi n th haiả ầ ự ệ ứ
c. Ph n t th ba ph i đ c hoán v v i ph n t l n th ba c a m ng. Hình 12.6 bi u di n m ngầ ử ứ ả ượ ị ớ ầ ử ớ ứ ủ ả ể ễ ả
sau khi hoán v ph n t l n th ba.ị ầ ử ớ ứ
90 70 60 10 40
Hình 12.6: M ng sau l n th c hi n th baả ầ ự ệ ứ
d. Ph n t th t ph i đ c hoán v v i ph n t l n th t c a m ng. Hình 12.7 bi u di n m ngầ ử ứ ư ả ượ ị ớ ầ ử ớ ứ ư ủ ả ể ễ ả
sau khi hoán v ph n t l n th t .ị ầ ử ớ ứ ư
90 70 60 40 10
Hình 12.7: M ng sau l n th c hi n th tả ầ ự ệ ứ ư
e. Hình 12.7 cũng bi u di n m ng đã đ c s p x p.ể ễ ả ượ ắ ế
Đ l p trình cho bài toán này, chúng ta c n hai vòng l p, m t đ tìm ph n t l n nh t trong m ngể ậ ầ ặ ộ ể ầ ử ớ ấ ả
và m t vòng l p kia đ l p quá trình th c hi n n l n. Th c ch t quá trình ph i l p n-1 l n cho m tộ ặ ể ặ ự ệ ầ ự ấ ả ặ ầ ộ
ph n t c a m ng b i vì ph n t cu i cùng s không còn ph n t nào đ so sánh v i nó. Vì v y,ầ ử ủ ả ở ầ ử ố ẽ ầ ử ể ớ ậ
chúng ta khai báo hai bi n i và j đ thao tác v i hai vòng l p ế ể ớ ặ for. Vòng l p ặfor v i ch s i đ cớ ỉ ố ượ
dùng đ l p l i quá trình xác đ nh ph n t l n nh t trong ph n còn l i c a m ng. Vòng l p ể ặ ạ ị ầ ử ớ ấ ầ ạ ủ ả ặ for v iớ
ch s j đ c dùng đ tìm ph n t l n th i c a m ng trong các ph n t t ph n t th i+1 đ nỉ ố ượ ể ầ ử ớ ứ ủ ả ầ ử ừ ầ ử ứ ế
ph n t cu i cùng c a m ng. Theo cách đó, ph n t l n th nh t th i trong ph n còn l i c aầ ử ố ủ ả ầ ử ớ ứ ấ ứ ầ ạ ủ
m ng s đ c đ a vào v trí th i.ả ẽ ượ ư ị ứ
Đo n mã l nh khai báo ch s và vòng l p th c hi n n - 1 l n v i i nh là ch s :ạ ệ ỉ ố ặ ự ệ ầ ớ ư ỉ ố
int i,j;
for(i = 0; i < n - 1; i++)
{
M ngả171
num
i=0 i=4
num
i=0 i=4
num
i=0 i=4
num
i=0 i=4
i=0 i=4
num
40
90

King.P
Đo n mã l nh cho vòng l p t ph n t th i + 1 đ n ph n t th n c a m ng:ạ ệ ặ ừ ầ ử ứ ế ầ ử ứ ủ ả
for(j = i + 1; j < n; j++)
{
Đ hoán v hai ph n t trong m ng chúng ta c n s d ng m t bi n t m. B i vì đây là th i đi mể ị ầ ử ả ầ ử ụ ộ ế ạ ở ờ ể
m t ph n t c a m ng đ c sao chép thành m t ph n t khác, giá tr trong ph n t th hai s bộ ầ ử ủ ả ượ ộ ầ ử ị ầ ử ứ ẽ ị
m t. Đ tránh m t giá tr c a ph n t th hai, giá tr c n ph i đ c l u l i trong m t bi n t m.ấ ể ấ ị ủ ầ ử ứ ị ầ ả ượ ư ạ ộ ế ạ
Đo n mã l nh đ hoán v ph n t th i v i ph n t l n nh t trong ph n còn l i c a m ng là:ạ ệ ể ị ầ ử ứ ớ ầ ử ớ ấ ầ ạ ủ ả
if(desnum[i] < desnum[j])
{
temp = desnum[i];
desnum[i] = desnum[j];
desnum[j] = temp;
}
}
}
Các vòng l p for c n đ c đóng l i và vì v y hai d u ngo c đóng xu t hi n trong đo n mã l nhặ ầ ượ ạ ậ ấ ặ ấ ệ ạ ệ
trên.
5. Hi n th m ng đã đ c s p x p.ể ị ả ượ ắ ế
Ch s i có th đ c dùng đ hi n th các giá tr c a m ng nh các câu l nh trình bày bên d i:ỉ ố ể ượ ể ể ị ị ủ ả ư ệ ướ
for(i = 0; i < n; i++)
printf("\n Number at [%d] is %d", i, desnum[i]);
Theo cách đó các ph n t c a m t m ng đ c s p x p. Hãy xem ch ng trình hoàn thi n d iầ ử ủ ộ ả ượ ắ ế ươ ệ ướ
đây.
1. G i trình so n th o mà b n có th vi t ch ong trình C.ọ ạ ả ạ ể ế ư
2. T o m t t p tin m i.ạ ộ ậ ớ
3. Đ a vào mã l nh sau:ư ệ
void main()
{
int n;
int num[100];
int l;
int desnum[100], k;
int i, j, temp;
printf("\nEnter the total number of marks to be entered : “);
scanf(“%d”, &n);
clrscr();
for (l = 0; l < n; l++)
{
printf(“\n Enter the marks of student %d : ”, l + 1);
scanf(“%d”, &num[l]);
}
for(k = 0; k < n; k++)
desnum[k] = num[k];
172 L p trình c b n Cậ ơ ả
Nguyen DInh Phuong
for(i = 0; i < n - 1; i++)
{
for(j = i + 1; j < n; j++)
{
if(desnum[i] < desnum[j])
{
temp = desnum[i];
desnum[i] = desnum[j];
desnum[j] = temp;
}
}
}
for(i = 0; i < n; i++)
printf("\n Number at [%d] is %d", i, desnum[i]);
}
Đ xem k t qu , th c hi n theo các b c li t kê d i đây:ể ế ả ự ệ ướ ệ ướ
4. L u t p tin v i tên arrayI.C.ư ậ ớ
5. Biên d ch t p tin, arrayI.C.ị ậ
6. Th c thi ch ng trình, arrayI.C.ự ươ
7. Tr v trình so n th o.ở ề ạ ả
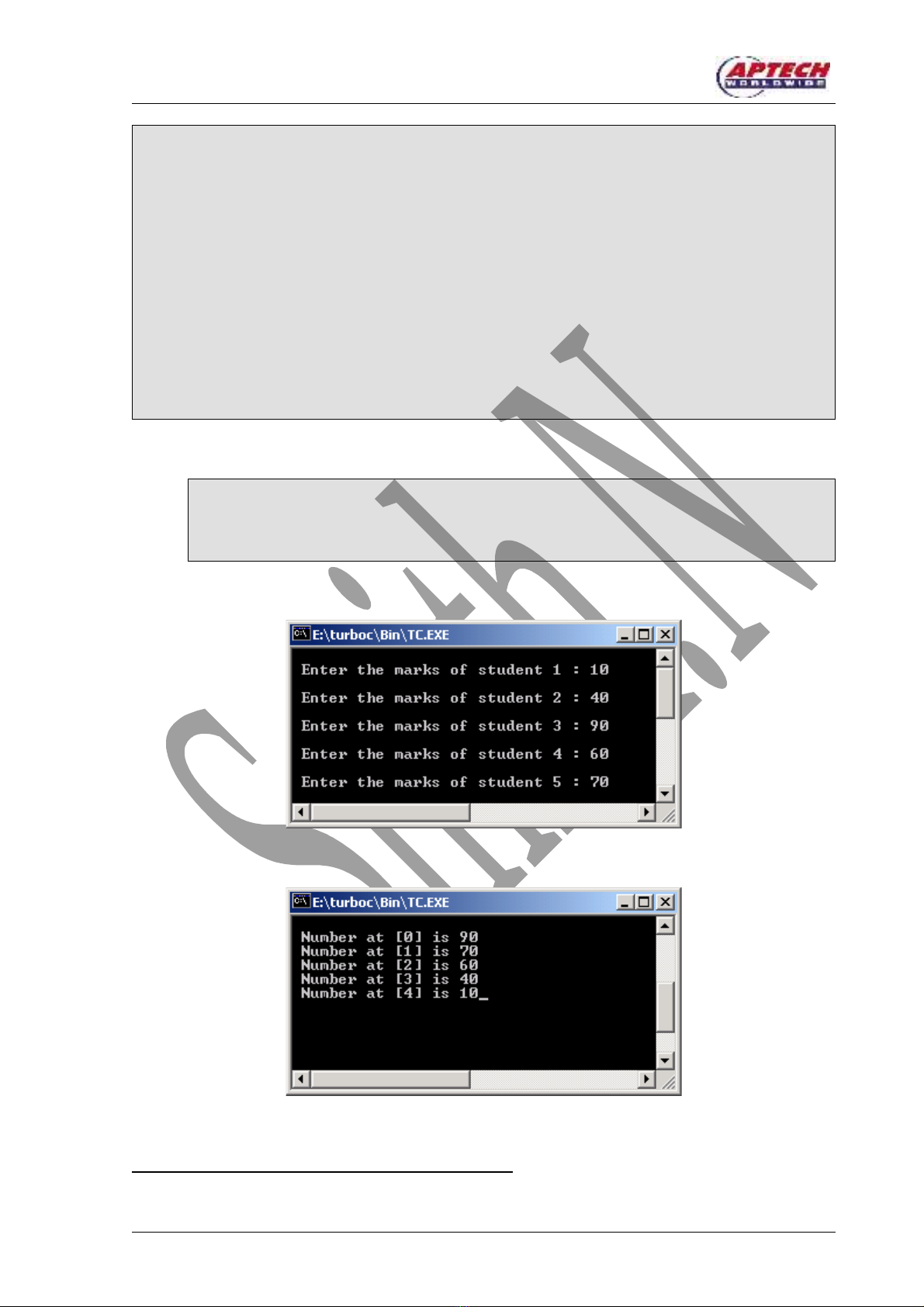
Ví d v k t qu th c thi c a ch ng trình trên đ c trình bày trong hình 12.8 và 12.9.ụ ề ế ả ự ủ ươ ượ
Hình 12.8: K t qu xu t I c a arrayI.C - Nh p vào các giá trế ả ấ ủ ậ ị
Hình 12.9 : K t qu xu t II c a arrayI.C – Xu t ra các giá trế ả ấ ủ ấ ị
12.1.2 C ng ma tr n s d ng các m ng hai chi uộ ậ ử ụ ả ề
M ngả173


























