
1
B GIÁO DC VÀ ĐÀO TO
ĐI HC ĐÀ NNG
H TH L SƯƠNG
NGHIÊN CU VÀ NG DNG PHN MM TOÁN HC
TRONG DY VÀ HC THNG KÊ
Chuyên ngành: Phương pháp Toán sơ cp
Mã s: 60.46.40
TÓM TT LUN VĂN THC SĨ KHOA HC
Đà Nng, Năm 2012
2
Công trình ñưc hoàn thành ti
ĐI HC ĐÀ NNG
Ngưi hưng dn khoa hc: PGS.TSKH. TRN QUC CHI N
Phn bin 1: PGS.TS. NGUY!N CHÁNH TÚ
Phn bin 2: PGS.TS. TRN ĐO DÕNG
Lun văn ñưc bo v ti Hi ñng bo v chm Lun
văn tt nghip Thc sĩ Khoa hc hp ti Đi hc Đà Nng vào
ngày 01 tháng 07 năm 2012.
Có th tìm hiu lun văn ti:
- Trung tâm Thông tin - Hc liu, Đi hc Đà Nng
- Thư vin Trưng Đi hc Sư Phm,Đi hc Đà Nng.

3
M" ĐU
1. LÝ DO CHN Đ TÀI.
Môn Xác sut thng kê ñưc ñánh giá là mt môn khó vi c
ngưi dy ln ngưi hc. Câu hi ñt ra là: làm th nào ñ vic dy và
hc môn Xác sut thng kê tr nên thun li hơn? Có hiu qu hơn?
Maple là mt phn mm Toán hc có kh năng ng d ng hu ht
các ni dung c!a môn Toán không nh"ng trong nhà trưng ph# thông mà
còn trong các trưng ñi hc và cao ñ$ng. Vi kh năng tính toán, minh
ha c!a mình, Maple là công c rt tt, giúp cho giáo viên, hc sinh và
sinh viên thun li cho vic tìm hiu và hc tp môn Toán.
Trên cơ s ñó, tôi ñã chn ñ tài “Nghiên cu và ng d ng
phn mm toán hc trong dy và hc thng kê”.
2. ĐI TƯ#NG VÀ PHM VI NGHIÊN CU.
2.1. Đi tưng.
- Các tài liu v xác sut thng kê và tài liu v maple.
2.2. Phm vi nghiên c$u.
- Các ng d ng c!a maple trong vic dy thng kê.
3. MC TIÊU VÀ NHIM V.
3.1. M%c tiêu.
- Giúp ngưi hc n%m ñưc các tính năng cơ bn c!a maple
và các ng d ng c!a nó trong hc phn thng kê.
3.2. Nhi&m v%.
- H thng mt s kin thc cơ bn c!a xác sut thng kê và
maple ñ làm cơ s cho vic nghiên cu ng d ng c!a maple trong
ging dy phn thng kê.
4. PHƯƠNG PHÁP NGHIÊN CU.
- T#ng hp và phân tích theo cu trúc logic c!a các tài liu thu
thp ñưc.
4
- So sánh, ñi chiu các tài liu liên quan.
- Thit k chương trình.
5. K T QU' D( KI N.
- S& tr thành mt tài liu tham kho b# ích cho ngưi dy và
ngưi hc trong phn hc thng kê thuc môn hc Toán kinh t và
Lý thuyt xác sut thng kê.
6. Ý NGHĨA KHOA HC VÀ Ý NGHĨA TH(C TI!N.
6.1. Ý nghĩa khoa hc.
- Góp mt phn nh trong vic nghiên cu maple ñ nh'm ci tin
phương pháp dy hc trong trưng ph# thông, cao ñ$ng và ñi hc.
6.2. Ý nghĩa th*c ti+n.
- Vn d ng trong công vic ging dy c!a bn thân trong
trưng cao ñ$ng.
7. THC NGHIM SƯ PHM.
- Tính linh ñng và mm d(o: ngưi hc b) thu hút bi nh"ng
thông tin và quá trình x* lý thông tin trên máy tính, t+ ñó truy tìm
nguyên nhân vn ñ.
- Tính h thng: ngưi hc có th ñiu ch,nh nhn thc c!a
mình trong h thng kin thc ñ n%m ñưc vn ñ, ñiu hòa nh"ng
mâu thun gi"a s- hoang mang bi ri trưc vn ñ mi và tính tò
mò mun khám phá.
8. C,U TRÚC C-A LUN VĂN.
Ngoài phn m ñu, kt lun và tài liu tham kho trong lun
văn gm có các chương như sau :
CHƯƠNG 1. T0NG QUAN V1 XÁC SU2T TH3NG KÊ
CHƯƠNG 2. GI4I THI5U V1 MAPLE
CHƯƠNG 3. 6NG DNG MAPLE TRONG DY TH3NG KÊ

5
CHƯƠNG 1
T.NG QUAN V XÁC SU,T THNG KÊ
1.1. XÁC SU,T.
1.1.1.Nh/ng khái ni&m cơ b0n v1 xác sut.
Đ2nh nghĩa 1.1.1.1 Khi quan sát mt hin tưng t- nhiên hay làm
mt thí nghim và chú ý ñn kt qu c!a hin tưng hay thí nghim
ñó. Khi ñó ta nói r'ng ñã th-c hin mt phép th*.
- Kt qu ñơn gin nht ñưc gi là bin c sơ cp.
- Tp hp gm tt c các bin c sơ cp ñưc gi là không
gian các bin c sơ cp. Ta thưng dùng:
ω
ñ ký hiu bin c sơ cp;
Ω
ñ ký hiu không gian bin c sơ cp;
A, B, C,… ñ ký hiu bin c.
1.1.2. Xác sut c3a bi4n c.
Đ2nh nghĩa 1.1.2.1.( Đ)nh nghĩa xác sut theo c# ñin)
Gi s* phép th* có n bin c ñng kh năng có th xy ra,
trong ñó có m trưng hp ñng kh năng thun li cho bin c A.
Khi ñó xác sut c!a A, ký hiu P(A) ñưc ñ)nh nghĩa b'ng công thc
sau:
= =
1.1.3. Bi4n ngu nhiên và hàm phân phi.
Đ2nh nghĩa 1.1.3.1 Cho không gian xác sut
Ω
F
. Hàm s
Ω →
ñưc gi là bin ngu nhiên nu X là hàm ño ñưc trên
σ
- ñi s Borel, tc là
ω ω
ω
−
∈Ω < ∈
∀ ∈
F
! " # .
Đ2nh nghĩa 1.1.3.2 Gi s* X là bin ngu nhiên xác ñ)nh trên
Ω
F
, nhn giá tr) trên
. Hàm s
6
$ %
= = < ∈
ñưc gi là hàm phân phi c!a bin ngu nhiên X.
Đ2nh nghĩa 1.1.3.3. Bin ngu nhiên X ñưc gi là bin ngu nhiên
ri rc nu tp hp các giá tr) c!a X có h"u hn hoc vô hn ñm
ñưc các phn t*.
Bng phân b xác sut ca X
ñây
&
> =
≠ ≠
∑
Hàm phân phi xác sut c!a X lúc này ñưc xác ñ)nh bi
< <
= = =
∑ ∑
Đ2nh nghĩa 1.1.3.4. Bin ngu nhiên X ñưc gi là bin ngu nhiên
liên t c nu hàm phân phi c!a nó liên t c, tương ñương vi tn ti
mt hàm s
→
kh tích không âm sao cho vi mi
∈
,
−∞
=
∫
trong ñó F(t) là hàm phân phi c!a X. Khi ñó, f(x) ñưc gi là hàm
mt ñ c!a X.
1.1.4. Phân v2 m$c xác sut
α
.
Đ2nh nghĩa 1.1.4.1 Phân v) mc xác sut
α
c!a bin ngu nhiên liên
t c X là s
α
sao cho
α
α
=
<
(*)
X
P
x
1
p
1
x
2
p
2
x
i
p
i
…
…
…
…
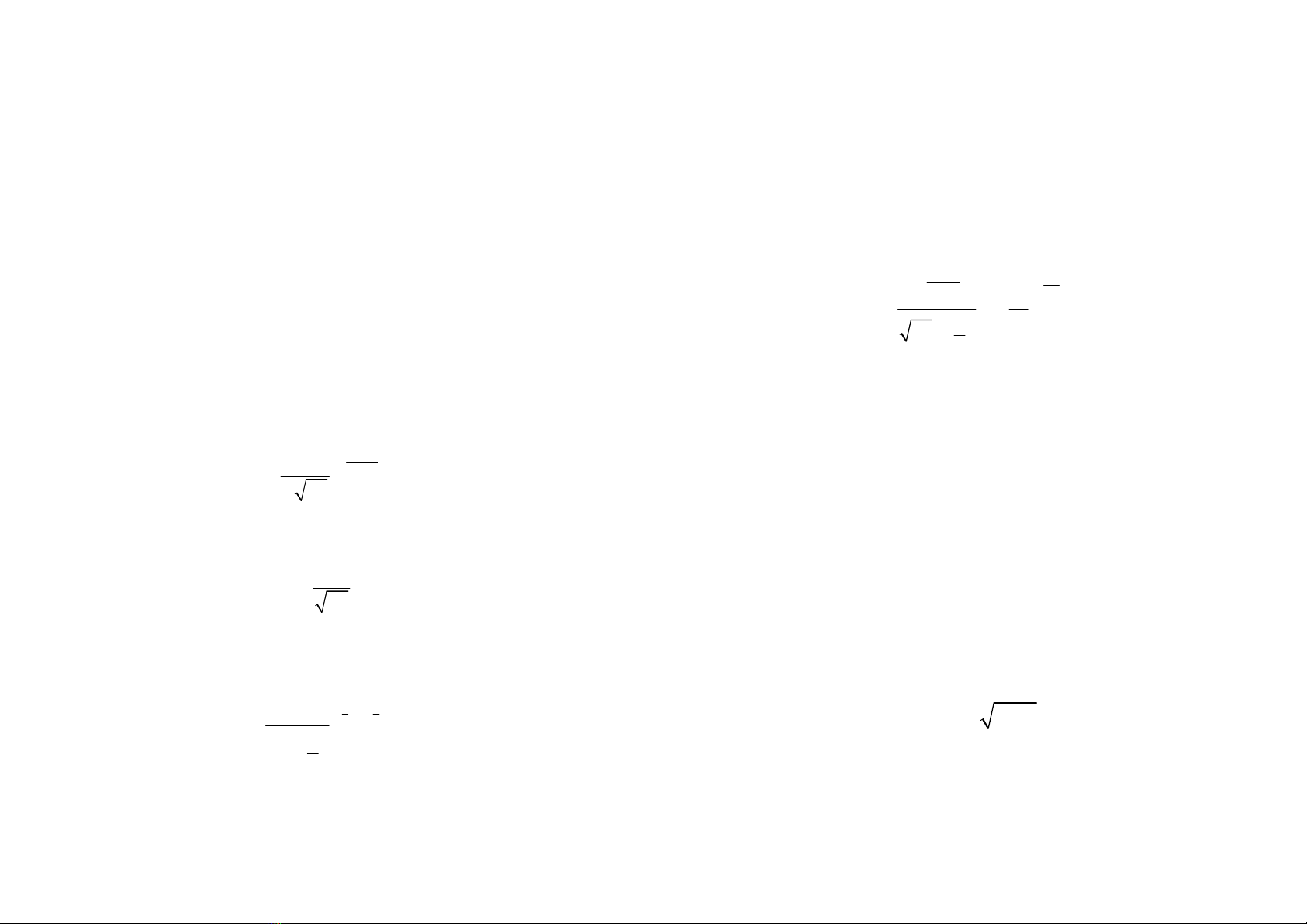
7
H thc (*) tương ñương vi
α
α
−∞
=
∫
Như vy,
α
là cn trên c!a tích phân sao cho tích phân b'ng
α
(hay
α
là v) trí cnh phi c!a hình thang cong sao cho din tích
hình thang cong b'ng
α
).
Mc khác, t+ h thc (*) suy ra
α
α
α
α
−
=
=
.
1.1.5. M5t s phân phi xác sut quan trng.
Đ2nh nghĩa 1.1.5.1 (Phân phi nh) thc)
Đ2nh nghĩa 1.1.5.2 (Phân phi Poisson).
Đ2nh nghĩa 1.1.5.3 (Phân phi chu7n).
Bin ngu nhiên X ñưc gi là có phân phi chu7n vi các
tham s
&
µ σ σ
>
(còn vit
'
µ σ
), nu hàm mt ñ c!a
nó có dng
'
'
'
'
µ
σ
σ π
−
−
∈
=
Phân phi N(0,1) còn ñưc gi là phân phi chu7n chính t%c, khi
ñó hàm mt ñ c!a nó có dng
'
'
'
π
−
∈
=
Đ2nh nghĩa 1.1.5.4 (Phân phi khi bình phương).
Bin ngu nhiên liên t c X ñưc gi là có phân phi khi bình
phương n bc t- do nu có hàm mt ñ.
' '
'
&
''
& &
− −
>
Γ
≤
=
8
Trong ñó
&
∞− −
Γ =
∫ gi là hàm Gamma.
Ký hiu
'
χ
.
Đ2nh nghĩa 1.1.5.5 (Phân phi Student).
Bin ngu nhiên liên t c X ñưc gi là có phân phi Student n
bc t- do nu nó có hàm mt ñ
''
'
'
π
+
−
+
Γ
+ ∀ ∈
Γ
=
Ký hiu
1.1.6. Các tham s ñ6c trưng c3a bi4n ngu nhiên.
Đ2nh nghĩa 1.1.6.1 Gi s* X là mt bin ngu nhiên xác ñ)nh trên
mt không gian xác sut
Ω
F
, ta gi s
Ω
=
∫
là kì vng (hay giá tr) trung bình c!a X).
Đ2nh nghĩa 1.1.6.2 Gi s* X là bin ngu nhiên và tn ti E(X). Khi
ñó, ñi lưng
2
( ) ( ( ))
= −
D X E X E X
h"u hn ñưc gi là phương sai c!a X.
Đ2nh nghĩa 1.1.6.3 Gi s* X là bin ngu nhiên và tn ti D(X). Khi
ñó ñi lưng
σ
=
ñưc gi ñ lch chu7n c!a X.
Đ2nh nghĩa 1.1.6.4 Mod c!a bin ngu nhiên X, ký hiu X
mod
là giá
tr) c!a bin ngu nhiên mà ti ñó phân phi ñt giá tr) ln nht.
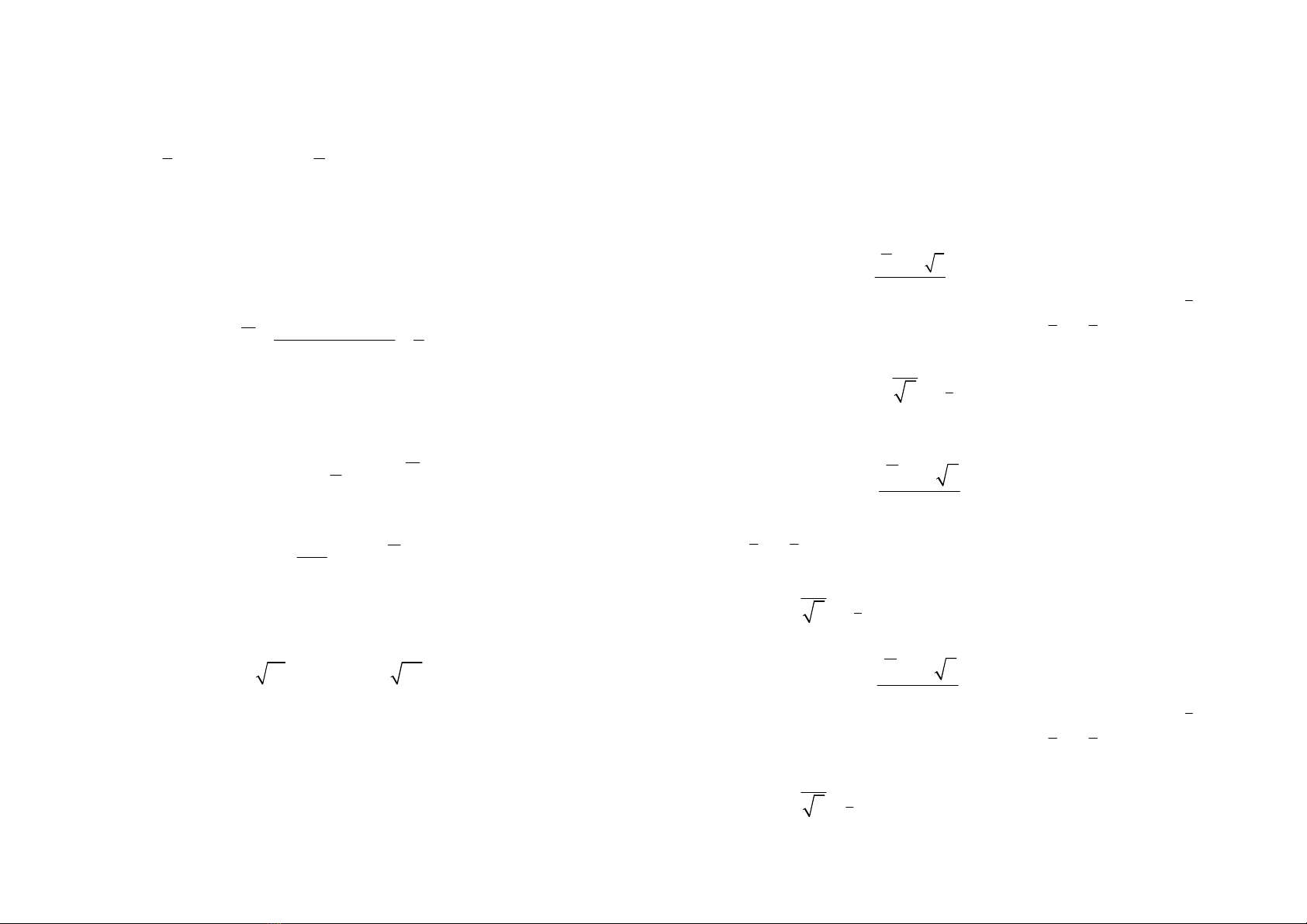
9
Đ2nh nghĩa 1.6.5 Med (s trung v)) c!a bin ngu nhiên X, ký hiu
X
med
là giá tr) c!a bin ngu nhiên mà ti ñó giá tr) c!a hàm phân
phi b'ng
'
, nghĩa là
'
=
.
1.2. THNG KÊ.
1.2.1. Lý thuy4t mu.
1.2.2 Các tham s ñ6c trưng.
Đ2nh nghĩa 1.2.2.1 Gi s* cho (X
1
, X
2
, …, X
n
) là mu ngu nhiên t+
phân phi F(x). Ta gi :
1 2
1
1
...
=
+ + +
= =
∑
n
n
i
i
n
X X X
X X
n
là trung bình mu.
Đ2nh nghĩa 1.2.2.2 Gi s* cho (X
1
, X
2
, …, X
n
) là mu ngu nhiên t+
phân phi F(x). Ta gi
2
2
1
( )
1
S ( )
=
= −
∑
n
i
i
X
X X
n
là phương sai chưa ñiu ch,nh và gi
2
'
2
1
( )
1
S ( )
1
=
= −
−∑
n
i
i
X
X X
n
là phương sai có ñiu ch,nh.
Đ2nh nghĩa 1.2.2.3 Gi s* cho (X
1
, X
2
, …, X
n
) là mu ngu nhiên t+
phân phi F(x). Ta gi
2 ' '2
= =
S S S
S
là ñ lch tiêu chu7n mu và ñ lch tiêu chu7n ñiu ch,nh mu.
10
1.2.3. Ưc lưng.
Bài toán ưc lưng kho0ng ñi vi bi4n ngu nhiên có phân phi
chu7n.
Ưc lưng khong kỳ vng ca bin ngu nhiên có phân phi
chun.
o Trưng hp phương sai ñã bit.
Chn thng kê
(
&
µ
σ
−
=
Th-c hin phép th* ñ có mu c th
(
)
1 2
, ,...,
n
x x x
, tính ñưc
x
, ta
tìm ñưc khong ưc lưng c!a kỳ vng là
)
ε ε
− +
.
Vi ñ chính xác
'
(
α
σ
ε
−
= .
o Trưng hp phương sai chưa bit.
*&
≥
.
Chn thng kê
+
(
&
µ
−
=
Khi ñó, ta cũng tìm ñưc khong ưc lưng c!a kỳ vng là
)
ε ε
− +
.
Vi
+
'
(
α
ε
−
=
*&
<
.
Chn thng kê +
(
µ
−
= −
Th-c hin phép th* ñ có mu c th
(
)
1 2
, ,...,
n
x x x
, tính ñưc
x
, ta
tìm ñưc khong ưc lưng c!a kỳ vng là
)
ε ε
− +
.
Vi
+
'
α
ε
−
−
=


























