Ứng dụng Autodesk Alias Studio để xây dựng bề mặt Class-A trong
thiết kế ngược các chi tiết chất lượng cao
Lê Văn Dũng 1
Trường Cơ khí - Ô Tô, Đại học Công nghiệp Hà Nội
Tóm tắt: Bài báo trình bày quy trình ứng dụng công nghệ Class-A Surface
Modeling bằng phần mềm Autodesk Alias Studio cho thiết kế ngược các chi tiết chất
lượng cao trong công nghiệp ô tô và sản phẩm tiêu dùng. Quy trình được xây dựng từ
dữ liệu quét 3D của chi tiết cản sau trên mô hình xe Porsche Macan 2013, qua các giai
đoạn xác định patch layout, dựng đường curve cơ sở, tạo bề mặt chính và bề mặt
chuyển tiếp, đến xuất dữ liệu sang các phần mềm kỹ thuật như CATIA, NX. Việc kiểm
soát liên tục hình học (G0, G1, G2), sử dụng các công cụ đánh giá chất lượng bề mặt
(Curvature Evaluation, Zebra Analysis, Deviation Map) giúp đảm bảo chi tiết đạt tiêu
chuẩn Class-A, phù hợp cho sản xuất hàng loạt. Kết quả thiết kế ngược cho thấy kết
quả tốt với đạt sai lệch dưới 0.2mm so với dữ liệu quét gốc và 100% ranh giới patch
đạt liên tục G2.
Từ khóa:`CAS, Class-A Surface, thiết kế ngược, Autodesk Alias, Bézier
1. Introduction
Trong bối cảnh toàn cầu hóa và sự phát triển mạnh mẽ của ngành công nghiệp
chế tạo, đặc biệt là trong lĩnh vực ô tô và các sản phẩm tiêu dùng cao cấp, chất lượng
bề mặt của các chi tiết sản phẩm ngày càng được xem là yếu tố then chốt quyết định
giá trị thương hiệu và năng lực cạnh tranh trên thị trường
[
1
] [
2
]
. Các hãng sản xuất lớn
không chỉ đòi hỏi độ chính xác về kích thước, mà còn yêu cầu sự hoàn hảo về mặt
thẩm mỹ, tính liên tục hình học và độ liền lạc tuyệt đối giữa các vùng bề mặt.
Class-A Surface`đại diện cho tiêu chuẩn chất lượng cao nhất của bề mặt ba chiều
trong thiết kế công nghiệp, được định nghĩa bởi ba yếu tố cốt lõi: (1) Độ chính xác
hình học tuyệt đối với khả năng liên tục G0 (vị trí), G1 (tiếp tuyến), G2 (độ cong) hoàn
hảo giữa các patch bề mặt; (2) Chất lượng thẩm mỹ vượt trội, đảm bảo phản xạ ánh
sáng mượt mà, không xuất hiện vết gãy, gợn sóng hay bất thường trên bề mặt; (3) Khả
năng sản xuất tối ưu, phù hợp với các công nghệ gia công hiện đại.
[
4
]
Trong lĩnh vực công nghiệp hiện đại, việc số hóa và phục dựng các chi tiết phức
tạp bằng thiết kế ngược (reverse engineering) đang ngày càng trở nên phổ biến, đặc
biệt trong các dự án phục chế linh kiện, nội địa hóa sản xuất và phát triển sản phẩm
mới
[
5,14
]
. Tuy nhiên, các sản phẩm thiết kế ngược truyền thống thường chỉ đáp ứng
được yêu cầu kỹ thuật mà chưa đạt được chất lượng thẩm mỹ cao do bề mặt không đạt
tiêu chuẩn Class-A. Để giải quyết vấn đề này, việc tích hợp các tiêu chí Class-A
Surface vào toàn bộ chu trình thiết kế ngược đã trở thành xu hướng tất yếu.
Autodesk Alias Studio đã khẳng định vị thế là phần mềm hàng đầu được tin dùng
bởi hầu hết các tập đoàn ô tô lớn nhất thế giới. Điển hình như các thương hiệu danh
tiếng BMW, Mercedes-Benz, Audi, Porsche, Volkswagen từ Đức; Ford Motor
Company và General Motors từ Mỹ; Toyota, Honda, Nissan từ Nhật Bản; Hyundai-Kia
từ Hàn Quốc; cùng với Volvo, Tesla và nhiều hãng xe cao cấp khác đều sử dụng Alias
làm công cụ chuẩn cho thiết kế tạo hình ngoại thất và phát triển bề mặt Class-A
[
6
]
. Các
nhà thiết kế tại các trung tâm R&D hàng đầu như BMW (Munich), Mercedes-Benz
(Stuttgart), Audi (Ingolstadt), Ford (Dearborn), và GM (Detroit) đều sử dụng Alias để
hỗ trợ toàn diện quy trình kiểm tra chất lượng hình học, đảm bảo các tiêu chí khắt khe
về liên tục G0, G1, G2, và kết nối liền mạch với các nền tảng CAD/CAM/PLM hiện
đại
[
7
]
.
Bài báo này trình bày quy trình tích hợp toàn diện các tiêu chí bề mặt Class-A
vào chu trình thiết kế ngược bằng Autodesk Alias Studio, nhằm tạo ra các mô hình số
không chỉ đảm bảo độ chính xác hình học từ dữ liệu quét 3D mà còn đạt giá trị thẩm
mỹ tối ưu, sẵn sàng cho sản xuất hàng loạt và truyền thông thương hiệu. Quy trình này,
đã được kiểm chứng tại các studio thiết kế danh tiếng và các trung tâm Advanced
Design của các OEM lớn, hứa hẹn sẽ mang lại giá trị thực tiễn trong thiết kế và phát
triển sản phẩm tại Việt Nam, đặc biệt trong việc tạo ra các sản phẩm có bề mặt đạt chất
lượng thẩm mỹ và kỹ thuật cao.
2. Cơ sở lý thuyết
2.1. Đường cong Bézier
Đường cong Bézier là một đường cong tham số (parametric curve) được sử dụng
phổ biến trong đồ họa máy tính và các lĩnh vực liên quan
[
3
]
. Đường cong Bézier được
đặt theo tên của kỹ sư người Pháp Pierre Bézier (1910–1999), người đã sử dụng nó
vào những năm 1960 để thiết kế các đường cong cho phần thân xe của hãng Renault
[
8
]
.
Một tập hợp rời rạc các điểm điều khiển được dùng để xác định nên một đường cong
mượt, liên tục thông qua một công thức toán học. Thông thường, đường cong này
được thiết kế nhằm xấp xỉ một hình dạng thực tế – đặc biệt trong trường hợp khó có
biểu diễn toán học chính xác hoặc biểu diễn đó quá phức tạp để xử lý trực tiếp.
Công thức toán học:
Trong đó:
B
(
t
)
: là vị trí của một điểm trên đường cong tại thời điểm ttt
Pi
: là các điểm điều khiển (control points), xác định hình dạng tổng thể
của đường cong
bi, n(t)
: là các đa thức cơ sở Bernstein, dùng làm trọng số để kết hợp các
điểm
Đa thức Bernstein được tính theo công thức:
bi, n (t)=(n
j)ti(1−t)n−12
Với:
(
n
j
)
=n!
i !(n−i)!:
là hệ số nhị thức (binomial coefficient)
t
∈
[0,1]: là tham số chạy liên tục từ 0 đến 1, điều khiển sự dịch chuyển
trên đường cong
Hình 1. Bézier curve với 4 điểm điều khiển
2.2. Bề mặt Bézier
Bề mặt Bézier là một dạng spline toán học được ứng dụng phổ biến trong đồ họa
máy tính, thiết kế có sự hỗ trợ của máy tính (CAD), và mô hình phần tử hữu hạn
(FEM). Tương tự như đường cong Bézier, bề mặt Bézier được xác định bởi một lưới
các điểm điều khiển. Mặc dù có nhiều điểm tương đồng với phép nội suy, điểm khác
biệt nổi bật là bề mặt không nhất thiết đi qua các điểm điều khiển trung tâm; thay vào
đó, hình dạng của nó được hướng về các điểm này như thể chịu ảnh hưởng bởi các
"lực hút" hình học. Nhờ khả năng biểu diễn bề mặt một cách mượt mà, dễ điều chỉnh
và chính xác, bề mặt Bézier trở thành một công cụ trực quan và hiệu quả trong các ứng
dụng thiết kế yêu cầu chất lượng hình học cao, đặc biệt là trong mô hình hóa bề mặt
Class-A
[
12
]
.
Một bề mặt Bézier cho trước có bậc (n,m) được xác định bởi một tập hợp (n+1)
(m+1) điểm điều khiển
ki , j
với i=0,...,n và j=0,...,m. Nó ánh xạ hình vuông đơn vị thành
một bề mặt trơn liên tục được nhúng trong không gian chứa các điểm
ki , j
- ví dụ, nếu
tất cả các
ki , j
đều là các điểm trong không gian bốn chiều, thì bề mặt sẽ nằm trong
không gian bốn chiều.
Một bề mặt Bézier hai chiều có thể được định nghĩa là một bề mặt tham số, trong
đó vị trí của một điểm p dưới dạng một hàm của các tọa độ tham số u, v được cho bởi:
[
4
]
P
(
u,v
)
=∑
i=0
n∑
j=0
m
ki , j . Bi
n
(
u
)
. Bi
m
(
v
)
(3)
P2
P3
P4
P0
Hình 2. Bề mặt Bézier bậc 4 theo phương uuu và bậc 3 theo phương
3. Quy trình tạo Surface Class-A từ file dữ liệu quét 3D
Dữ liệu quét ban đầu là một bản sao kỹ thuật số thô của mô hình vật lý, thường ở
dạng lưới tam giác hoặc đám mây điểm. Ví dụ như trong ngành công nghiệp ô tô,
nguồn gốc của dữ liệu này tương tự như là các mô hình đất sét (clay models) được tạo
ra thủ công bởi các nhà thiết kế
[
13,14
]
. Dữ liệu này chỉ là một bản ghi kỹ thuật số
"thô" của mô hình vật lý. Đặc điểm của loại dữ liệu này là sự thiếu hụt hoàn toàn các
thuộc tính hình học quan trọng: nó không có tính liên tục G0, G1, G2 và cấu trúc rời
rạc, không đồng nhất. Hơn nữa, dữ liệu quét luôn chứa sai số và nhiễu do quá trình thu
thập, dẫn đến bề mặt lởm chởm, không phẳng. Do những hạn chế này, dữ liệu quét ban
đầu không thể đáp ứng trực tiếp các yêu cầu về mặt thẩm mỹ lẫn kỹ thuật cho quy
trình sản xuất.
Trong bài báo này, tôi sử dụng dữ liệu quét 3D của chi tiết cản sau trên mô hình
xe Porsche Macan 2013 (Hình 3, 4) làm chi tiết thực hành. Đây là một chi tiết có hình
dạng phức tạp với nhiều đường cong và yêu cầu về kỹ thuật thẩm mỹ cao, rất phù hợp
để kiểm chứng hiệu quả của quy trình Class-A Surface Modeling trong ứng dụng thực
tế.
(a) (b)
Hình 3. Hình ảnh thực tế chi tiết cản sau trên mô hình xe Porsche Macan(a), dữ
liệu quét được hiển thị trên phần mềm Alias Studio(b)
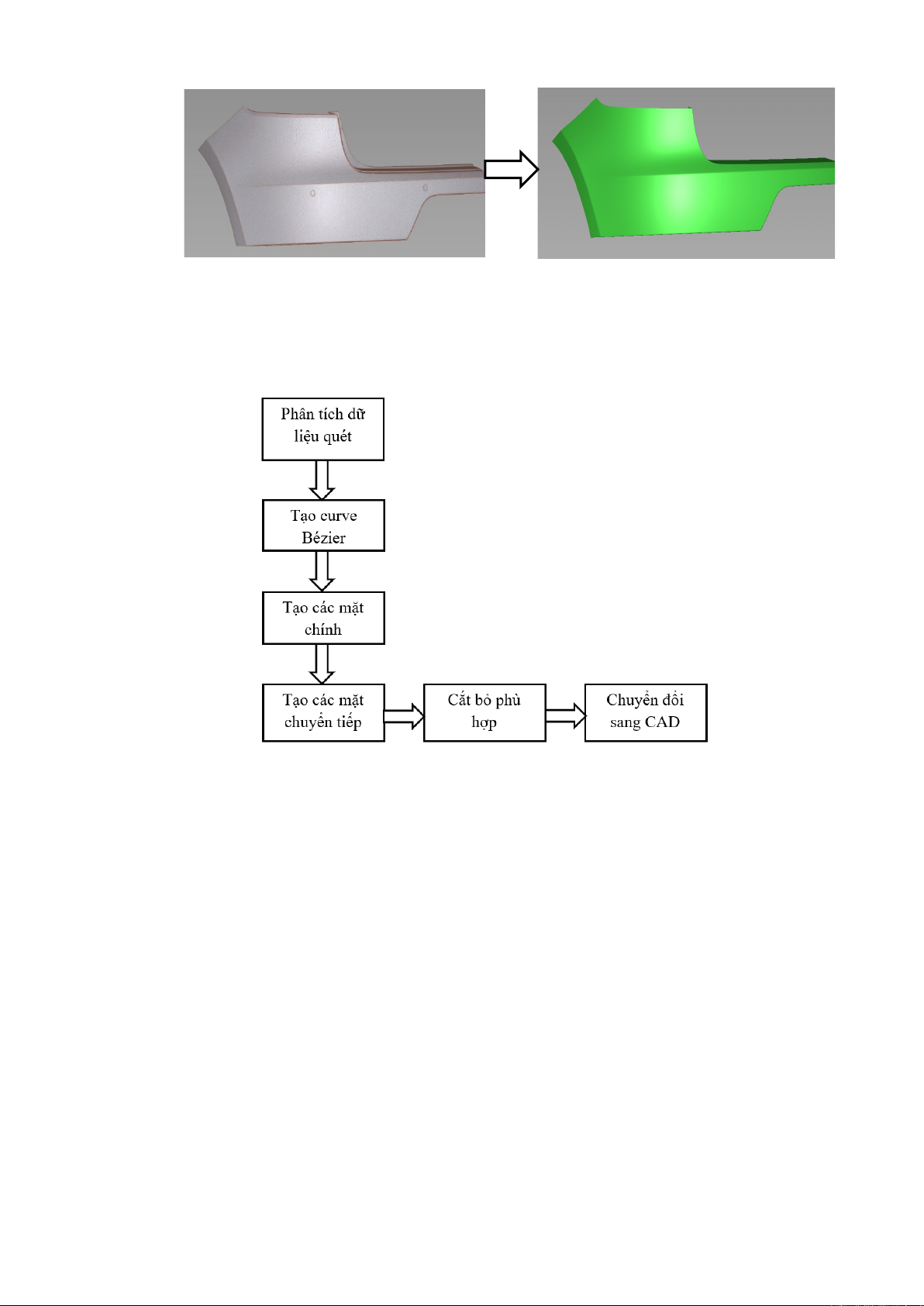
Dữ liệu quét Class A surface
Hình 4. Mô hình hóa bề mặt từ dữ liệu quét 3D
Dưới đây là sơ đồ tổng quát quy trình chuyển đổi từ dữ liệu quét 3D thành bề mặt
Class A (Hình 4) đã được được sử dụng trong bài báo này:
Hình 4. Quy trình tạo bề mặt Class A
4. RESULTS AND DISCUSSION
4.1. Nhận định Patch Layout trong quy trình tạo Surface Class-A
Trong giai đoạn đầu tiên của quy trình, nhận định patch layout là bước nền tảng
nhằm xác định cách chia nhỏ bề mặt tổng thể thành các vùng (patch) hợp lý. Việc bố
trí các patch hợp lý sẽ giúp kiểm soát tốt hơn hình học, giảm thiểu các lỗi cong, đồng
thời tối ưu hóa quá trình dựng và chỉnh sửa bề mặt.
Về mặt toán học, việc đánh giá độ cong của bề mặt được dựa trên các đặc trưng
của hình học vi phân. Tại mỗi điểm trên bề mặt trơn
S(u, v)
, tồn tại hai giá trị độ cong
chính
k1
và
k2
, đại diện cho độ cong cực đại và cực tiểu tại điểm đó, tương ứng với hai
phương chính vuông góc trong mặt tiếp tuyến
[
10
]
. Từ hai độ cong này, các đại lượng
hình học quan trọng được xác định như (4) and (5):
-Độ cong Gaussian (K):
K=k1.k 2
(4)