
Tuyển tập Hội nghị Khoa học thường niên năm 2024. ISBN: 978-604-82-8175-5
232
ỨNG DỤNG THUẬT TOÁN TIẾN HÓA VI PHÂN
TỰ THÍCH ỨNG AEpDE TRONG BÀI TOÁN TỐI ƯU
TIẾT DIỆN KẾT CẤU DÀN THÉP
Nguyễn Thị Thanh Thúy1, Nguyễn Mạnh Cường2
1Trường Đại học Thủy lợi, email: thuynt@tlu.edu.vn
2Viện Khoa học Công nghệ Xây dựng - IBST
1. GIỚI THIỆU CHUNG
Kết cấu thép được sử dụng phổ biến trong
công trình xây dựng dân dụng và công nghiệp
nhờ tính năng chịu lực tốt và khả năng tái chế
cao, đáp ứng nhu cầu phát triển bền vững. Tối
ưu hóa kết cấu thép mang lại hiệu quả kinh tế
đáng kể, đặc biệt khi giá thành vật liệu thép
ngày càng tăng cao. Bài toán tối ưu kết cấu
thép chủ yếu tập trung vào việc tối ưu tiết diện
thanh, một bài toán phức tạp với nhiều biến số
và yêu cầu phân tích kết cấu nhiều lần để
kiểm tra các điều kiện ràng buộc.
Trước những năm 1950, các bài toán này
thường được giải quyết bằng các phương
pháp cổ điển như phương pháp dựa trên độ
dốc (gradient), với sự hỗ trợ hạn chế từ các
công cụ tính toán. Các phương pháp này
thường chỉ áp dụng cho các bài toán kết cấu
đơn giản như bài toán dàn có số lượng thanh
hạn chế. Từ những năm 1950 trở đi, sự phát
triển của máy tính điện tử đã giúp các
phương pháp như quy hoạch tuyến tính trở
nên phổ biến. Đến thập niên 1970 và 1990,
các thuật toán metaheuristic như thuật toán di
truyền (GA), tiến hóa vi phân (DE) [1]...
được phát triển và ứng dụng rộng rãi, áp
dụng cho nhiều bài toán khác nhau như: hệ
giàn [2], hệ khung [3], nhà cao tầng [4].
Để tăng hiệu quả tối ưu hóa, các phương
pháp như phát triển các thuật toán mới hoặc
cải tiến thuật toán hiện có giúp nhanh chóng
tìm được nghiệm tối ưu và giảm bớt thời gian
cũng như tài nguyên tính toán. Trong nghiên
cứu này, tác giả trình bày hai thuật toán cải
tiến của DE là EpDE và AEpDE, áp dụng vào
tối ưu hóa một bài toán dàn phẳng để đánh giá
hiệu quả của chúng so với thuật toán gốc.
2. PHƯƠNG PHÁP NGHIÊN CỨU
Bài báo sử dụng phương pháp nghiên cứu
tổng hợp lý thuyết và lập trình bằng ngôn
ngữ python để điều khiển quá trình tối ưu tiết
diện kết cấu dàn thép.
Sau đây trình bày một số các nội dung
chính về thuật toán tối ưu DE và các thuật
toán cải tiến EpDE [3] và AEpDE [5].
2.1. Thuật toán tiến hóa vi phân DE
Thuật toán Tiến hóa Vi phân (Differential
Evolution - DE) là một phương pháp tối ưu
hóa dựa trên quần thể được sử dụng rộng rãi
trong các bài toán tối ưu hóa số học và kỹ
thuật. Với ưu điểm dễ dàng cài đặt và thực
hiện, DE đặc biệt phù hợp với các bài toán tối
ưu phức tạp nhờ khả năng tìm kiếm toàn cục
mạnh mẽ. Các bước thực hiện DE như sau:
(1) Quần thể ban đầu được tạo ra ngẫu nhiên
trong không gian tìm kiếm. Mỗi cá thể trong
quần thể đại diện cho một nghiệm tiềm năng
của bài toán. (2) Tạo vector đột biến: với mỗi
cá thể mục tiêu, một vector đột biến được tạo
ra bằng cách cộng một vector khác biệt (hiệu
của hai vector ngẫu nhiên trong quần thể) với
một vector thứ ba. (3) Lai ghép để tạo vector
thử nghiệm bằng cách kết hợp vector mục
tiêu và vector đột biến. (4) Chọn lọc theo
nguyên tắc: Vector thử nghiệm được so sánh
với vector mục tiêu và vector nào có giá trị
hàm mục tiêu tốt hơn sẽ được chọn cho thế
hệ tiếp theo. Quá trình tiến hóa qua nhiều thế

Tuyển tập Hội nghị Khoa học thường niên năm 2024. ISBN: 978-604-82-8175-5
233
hệ: đột biến, lai ghép và chọn lọc được lặp lại
cho đến khi đạt được tiêu chí dừng, ví dụ như
số thế hệ tối đa hoặc độ hội tụ mong muốn.
2.2. Thuật toán tiến hóa vi phân cải tiến
EpDE
EpDE là một biến thể đã được phát triển
và ứng dụng thành công trong đó sử dụng kỹ
thuật đột biến 'DE/ pbest/1' [5] để tạo ra cá
thể đột biến V bằng cách sử dụng một cá thể
ngẫu nhiên Xpbest trong số p100% cá thể tốt
nhất. Giá trị p ꞓ(0,1]- được kiểm soát một
cách hợp lý trong quá trình tối ưu để sử dụng
hiệu quả chiến lược khám phá tối ưu toàn cục
'DE/rand/1' ở giai đoạn đầu và chiến lược
'DE/best/1' với khả năng hội tụ nhanh và tìm
kiếm cục bộ tốt được áp dụng trong giai đoạn
sau của quá trình tối ưu. p được tính theo
công thức sau:
1
1
k
Btotal _ generation
pk A NP
NP, A và B là các tham số có thể kiểm soát
giá trị p trong quá trình tối ưu hóa. A kiểm
soát số cá thể tốt nhất được sử dụng lúc đầu.
B ảnh hưởng đến tốc độ giảm của giá trị p.
2.3. Thuật toán tiến hóa vi phân tự thích
ứng AEpDE
Giá trị p đề xuất trong EpDE phụ thuộc
vào số thế hệ tối đa được xác định trước
(total_generation) do đó sự thay đổi của giá
trị p không phản ánh chính xác tốc độ hội tụ
quần thể. Vì thế trong AEpDE, p đã được đề
xuất theo công thức để có thể thay đổi cùng
với mức độ đa dạng của quần thể:
1
0
TD t
BTD
pANP
D là số lượng biến thiết kế; xij là biến thiết
kế thứ jth của cá thể thứ ith; và TD(t) là chỉ số
đa dạng quần thể ở thế hệ tth biểu thị độ lệch
chuẩn trung bình của mỗi cá thể trong quần
thể [5].
2.4. Bài toán tối ưu tiết diện kết cấu
dàn thép
Trong bài toán tối ưu hóa tiết diện kết cấu
thanh dàn, mục tiêu là tối thiểu hóa tổng khối
lượng của toàn bộ thanh trong kết cấu. Bài
toán này thường có các điều kiện ràng buộc
liên quan đến ứng suất và chuyển vị theo quy
định của tiêu chuẩn thiết kế, đảm bảo rằng
các thanh không vượt quá giới hạn an toàn
cho phép. Phương pháp hàm phạt được áp
dụng để chuyển bài toán có ràng buộc thành
bài toán không ràng buộc, bằng cách thêm
hàm phạt vào hàm mục tiêu để xử lý vi phạm
ràng buộc, như mô tả trong tài liệu [5].
3. KẾT QUẢ NGHIÊN CỨU
Tác giả đã tiến hành lập trình với mã nguồn
gồm các khối điều khiển chương trình tối ưu
hóa gồm các mô đun là các hàm con như sau:
Nhập số liệu đầu vào cho hệ dàn; Các đặc
trưng vật liệu, tọa độ nút, thanh dàn, điều kiện
liên kết và tải trọng nút. Module phân tích kết
cấu dựa trên phần tử hữu hạn [6]. Mô đun tính
toán tối ưu gồm khởi tạo, tạo đột biến, lai
ghép, lựa chọn và kiểm tra các điều kiện ràng
buộc về ứng suất và chuyển vị từ đó tìm được
nghiệm quá trình tối ưu và cho thấy đường
cong hội tụ của từng thuật toán.
Bài toán áp dụng là bài toán dàn 10 thanh
được sử dụng rộng rãi làm bài toán chuẩn về
nghiên cứu tối ưu trong các tài liệu với các số
liệu như sau:
Hình 1. Số liệu và hình học
của kết cấu dàn 10 thanh
E = 6.89104 MPa;
= 2770kg/m3; Tại nút
2 và nút 4 chịu P1 = 445.4kN; chuyển vị cho
phép của nút [u] = 50.8mm; ứng suất cho
phép của thanh là [
] = 172.25MPa. Không
xét đến ràng buộc do mất ổn định do oằn. Tiết
diện thanh từ 64.62 mm2 đến 25806.4mm2.
Tuyển tập Hội nghị Khoa học thường niên năm 2024. ISBN: 978-604-82-8175-5
234
Bài toán tối ưu có 10 biến thiết kế, biến
liên tục, quần thể ban đầu được khởi tạo ngẫu
nhiên, chọn số cá thể ban đầu NP = 30, số thế
hệ chọn 600. Mỗi thuật toán chạy 10 lần để
lấy kết quả khối lượng dàn tốt nhất, trung
bình và kém nhất.
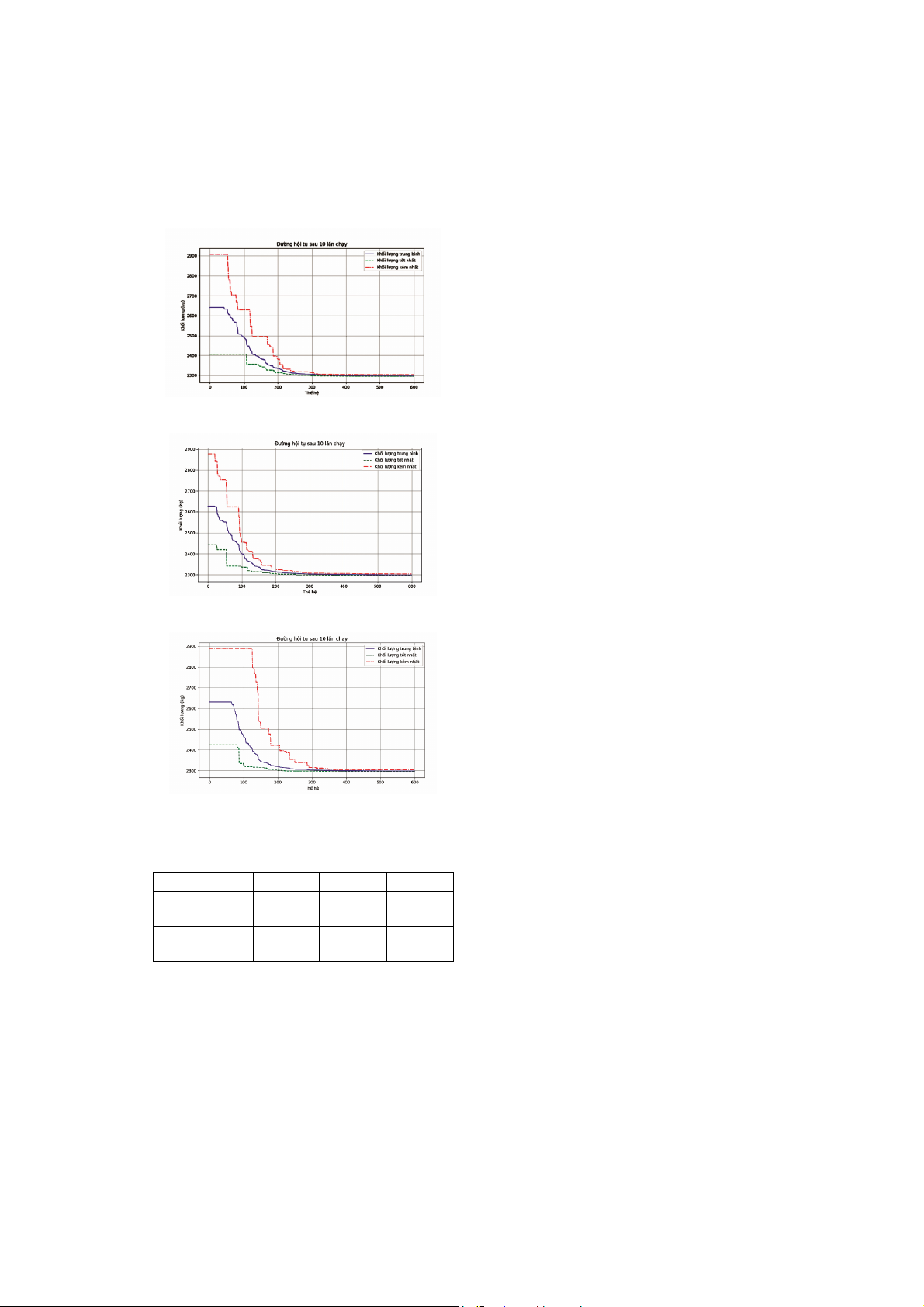
Kết quả về đường cong hội tụ của mỗi
thuật toán như sau:
Hình 2. Đường cong hội tụ cho DE
Hình 3. Đường cong hội tụ cho EpDE
Hình 4. Đường cong hội tụ cho AEpDE
Bảng 1. Các kết quả khối lượng dàn
sau 10 lần chạy của các thuật toán
Thuật toán DE EpDE AEpDE
Khối lượng tốt
nhất (kg) 2295.4 2295.4 2295.4
Khối lượng
trung bình (kg) 2300.32 2298.03 2299.05
4. KẾT LUẬN
Bài báo trình bày các thuật toán DE cải
tiến là EpDE và AEpDE khi áp dụng vào bài
toán tối ưu tiết diện dàn phẳng. Kết quả cho
thấy giá trị tổng khối lượng của dàn do các
thuật toán tính toán xấp xỉ nhau. Tuy nhiên,
hai thuật toán cải tiến cho thấy sự hội tụ
nhanh hơn so với thuật toán DE, đặc biệt
AEpDE cho tốc độ hội tụ nhanh nhất. Điều
này chỉ ra rằng đối với bài toán dàn, chiến
lược p-best có thể tìm kiếm nghiệm tối ưu
toàn cục tốt hơn với tốc độ hội tụ nhanh hơn.
Tuy nhiên, AEpDE chưa thể hiện được ưu
điểm trội hơn so với EpDE về khả năng tìm
kiếm nghiệm tối ưu toàn cục. Nghiên cứu chỉ
ra rằng cần tiếp tục phát triển và ứng dụng
các thuật toán này vào các công trình quy mô
lớn hơn để đánh giá một cách toàn diện khả
năng của chúng.
5. TÀI LIỆU THAM KHẢO
[1] Q.A Vu, T.S. Cao, H.H. Nguyen, V.H.
Truong, M.H. Ha. 2023. An efficient
differential evolution-based method for
optimization of steel frame structures using
direct analysis. Structures 51, 67-78.
[2] T.S. Cao, T.T.T. Nguyen, V.S. Nguyen,
V.H. Truong, H.H. Nguyen. 2023.
Performance of six metaheuristic algorithms
for multi-objective optimization of nonlinear
inelastic steel trusses. Buildings 13 (4), 868.
[3] V.H. Truong, H.M. Hung, P.H. Anh, T.D.
Hoc. 2020. Optimization of steel moment
frames with panel-zone design using an
adaptive differential evolution. Journal of
Science and Technology in Civil
Engineering (JSTCE) - HUCE, 14(2), 65-75.
[4] H.A. Pham, D.X. Nguyen, V.H. Truong.
2021. An efficient differential-evolution-
based moving compensation optimization
approach for controlling differential column
shortening in tall buildings. Expert Systems
with Applications 169, 114531.
[5] Nguyễn Thị Thanh Thúy. 2023. Luận án
Tiến sĩ. Trường Đại học Thủy lợi.

























![Quyển ghi Xác suất và Thống kê [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251030/anh26012006/135x160/68811762164229.jpg)
