
1
19 Phương pháp chứng minh Bất đẳng thức
PHẦN 1
CÁC KIẾN THỨC CẦN LƯU Ý
1/Định nghĩa
0
0
A B A B
A B A B
2/Tính chất
+ A>B AB
+ A>B và B >C CA
+ A>B
A+C >B + C
+ A>B và C > D
A+C > B + D
+ A>B và C > 0
A.C > B.C
+ A>B và C < 0
A.C < B.C
+ 0 < A < B và 0 < C <D
0 < A.C < B.D
+ A > B > 0
An > Bnn
+ A > B
A n > B n với n lẻ
+ A > B
A n > B n với n chẵn
+ m > n > 0 và A > 1
Am > A n
+ m > n > 0 và 0 <A < 1
Am < A n
+A < B và A.B > 0
B
A
11
3/Một số hằng bất đẳng thức
+ A 2
0 với
A ( dấu = xảy ra khi A = 0 )
+ An
0 với
A ( dấu = xảy ra khi A = 0 )
+ 0A với
A
(dấu = xảy ra khi A = 0 )
+ - A < A = A
+
A B A B
( dấu = xảy ra khi A.B > 0)
+ BABA ( dấu = xảy ra khi A.B < 0)

2
PHẦN II
CÁC PHƯƠNG PHÁP CHỨNG MINH BẤT ĐẲNG THỨC
Phương pháp 1 : Dùng định nghĩa
Kiến thức : Để chứng minh A > B. Ta lập hiệu A –B > 0
Lưu ý dùng hằng bất đẳng thức M2
0 với M
Ví dụ 1 x, y, z chứng minh rằng :
a) x2 + y2 + z2
xy+ yz + zx
b) x2 + y2 + z 2
2xy – 2xz + 2yz
c) x2 + y2 + z2+3
2 (x + y + z)
Giải:
a) Ta xét hiệu : x2 + y2 + z2- xy – yz – zx =
2
1.2 .( x2 + y2 + z2- xy – yz –
zx)
=
2
1
0)()()( 222 zyzxyx đúng với mọi x;y;z
R
Vì (x-y)2
0 vớix ; y Dấu bằng xảy ra khi x=y
(x-z)2
0 vớix ; z Dấu bằng xảy ra khi x=z
(y-z)2
0 với z; y Dấu bằng xảy ra khi z=y
Vậy x2 + y2 + z2
xy+ yz + zx. Dấu bằng xảy ra khi x = y =z
b)Ta xét hiệu: x2 + y2 + z 2- ( 2xy – 2xz +2yz ) = x2 + y2 + z 2- 2xy +2xz –
2yz
= ( x – y + z)20
đúng với mọi x;y;z
R
Vậy x2 + y2 + z 2
2xy – 2xz + 2yz đúng với mọi x;y;z
R
Dấu bằng xảy ra khi x+y=z
c) Ta xét hiệu: x2 + y2 + z 2+3 – 2( x+ y +z ) = x2- 2x + 1 + y2 -2y +1 + z 2-
2z +1
= (x-1)2+ (y-1) 2+(z-1)2
0. Dấu(=)xảy ra khi x=y=z=1
Ví dụ 2: chứng minh rằng :
a)
2
22
22
baba ; b)
2
222
33
cbacba c) Hãy tổng quát bài
toán
Giải:
a) Ta xét hiệu
2
22
22
baba
=
4
2
4
22222 bababa
=
abbaba 222
4
12222 =
0
4
12 ba
Vậy
2
22
22
baba . Dấu bằng xảy ra khi a=b
b)Ta xét hiệu

3
2
222
33
cbacba =
0
9
1222 accbba .Vậy
2
222
33
cbacba
Dấu bằng xảy ra khi a = b =c
c)Tổng quát
2
21
22
2
2
1........
n
aaa
n
aaa nn
Tóm lại các bước để chứng minh A
B theo định nghĩa
Bước 1: Ta xét hiệu H = A - B
Bước 2:Biến đổi H=(C+D) 2hoặc H=(C+D) 2+….+(E+F) 2
Bước 3:Kết luận A B
Ví dụ 1: Chứng minh m,n,p,q ta đều có : m 2+ n 2+ p 2+ q2+1 m(n+p+q+1)
Giải:
01
4444
2
2
2
2
2
2
2
m
m
qmq
m
pmp
m
nmn
m
01
2222
2222
m
q
m
p
m
n
m (luôn đúng)
Dấu bằng xảy ra khi
01
2
0
2
0
2
0
2
m
q
m
p
m
n
m
2
2
2
2
m
m
q
m
p
m
n
1
2
qpn
m
Ví dụ 2: Chứng minh rằng với mọi a, b, c ta luôn có : )(
444 cbaabccba
Giải: Ta có : )(
444 cbaabccba , 0,,
cba
0
0)2(
)2()2(
0222
222
0222222
0
222
2
22
2
22
2
22
22222
2222222222
2
22
2
22
2
22
222
22
2
2222
2
2222
2
22
222444
222444
acabacbcbcabaccbba
abaacba
abcaccbacbcbbaaccbba
abcacbbca
caaccbcbbaba
abcacbbcacba
abcacbbcacba
Đúng với mọi a, b, c.
Phương pháp 2 : Dùng phép biến đổi tương đương
Kiến thức:

4
Ta biến đổi bất đẳng thức cần chứng minh tương đương với bất đẳng thức
đúng hoặc bất đẳng thức đã được chứng minh là đúng.
Nếu A < B
C < D , với C < D là một bất đẳng thức hiển nhiên, hoặc đã biết là đúng
thì có bất đẳng thức A < B .
Chú ý các hằng đẳng thức sau:
22
22BABABA
BCACABCBACBA 222
222
2
3223
333 BABBAABA
Ví dụ 1: Cho a, b, c, d,e là các số thực chứng minh rằng
a) ab
b
a
4
2
2
b) baabba 1
22
c)
edcbaedcba 22222
Giải:
a) ab
b
a
4
2
2abba 44 22 044 22 baa
02 2 ba
(BĐT này luôn đúng). Vậy ab
b
a
4
2
2 (dấu bằng xảy ra khi 2a=b)
b) baabba 1
22
)(21(2 22 baabba
012122 2222 bbaababa
0)1()1()( 222 baba Bất đẳng thức cuối đúng.
Vậy baabba 1
22 . Dấu bằng xảy ra khi a=b=1
c)
edcbaedcba 22222
edcbaedcba 44 22222
044444444 22222222 cacadadacacababa
02222 2222 cadacaba
Bất đẳng thức đúng vậy ta có điều phải chứng minh
Ví dụ 2: Chứng minh rằng:
4488221010 babababa
Giải:
4488221010 babababa
128448121210221012 bbabaabbabaa
0
22822228 abbababa
a2b2(a2-b2)(a6-b6)
0
a2b2(a2-b2)2(a4+ a2b2+b4)
0
Bất đẳng thứccuối đúng vậy ta có điều phải chứng minh
Ví dụ 3: cho x.y =1 và x
y Chứng minh yx
yx
22
22
Giải: yx
yx
22
22 vì :x
y nên x- y
0
x2+y2
22 ( x-y)
x2+y2- 22 x+ 22 y
0
x2+y2+2- 22 x+ 22 y -2
0
x2+y2+( 2)2- 22 x+ 22 y -2xy
0 vì x.y=1 nên 2.x.y=2
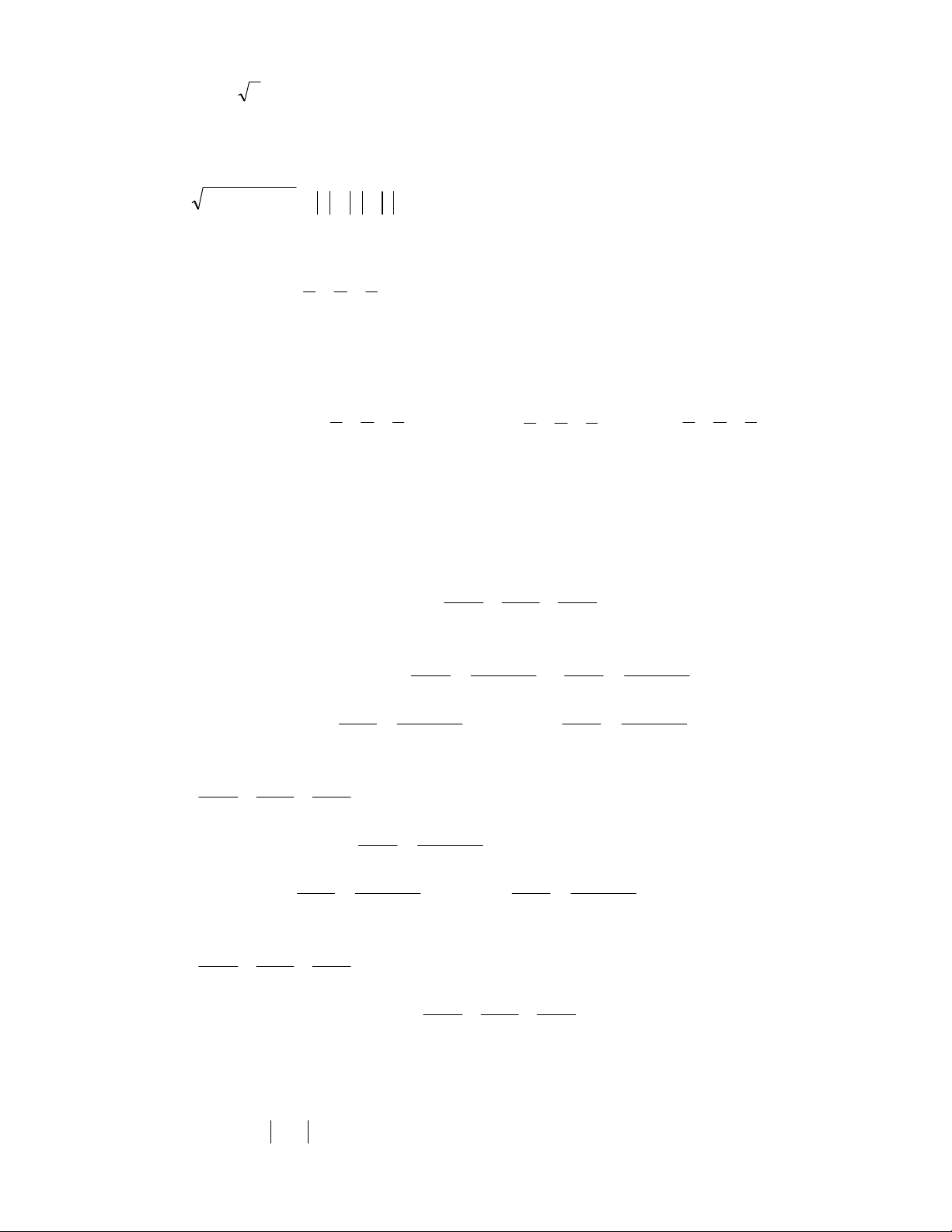
5
(x-y- 2)2
0 Điều này luôn luôn đúng . Vậy ta có điều phải chứng
minh
Ví dụ 4: Chứng minh rằng:
a/ P(x,y)= 01269 222 yxyyyx Ryx
,
b/ cbacba 222 (gợi ý :bình phương 2 vế)
c/ Cho ba số thực khác không x, y, z thỏa mãn:
zyx
zyx
zyx
111
1..
Chứng minh rằng :có đúng một trong ba số x,y,z lớn hơn 1
Giải: Xét (x-1)(y-1)(z-1)=xyz+(xy+yz+zx)+x+y+z-1
=(xyz-1)+(x+y+z)-xyz( zyx
111 )=x+y+z - ( 0)
111 zyx (vì zyx
111 < x+y+z
theo gt)
2 trong 3 số x-1 , y-1 , z-1 âm hoặc cả ba sỗ-1 , y-1, z-1 là dương.
Nếu trường hợp sau xảy ra thì x, y, z >1
x.y.z>1 Mâu thuẫn gt x.y.z=1
bắt buộc phải xảy ra trường hợp trên tức là có đúng 1 trong ba số x ,y ,z là số lớn
hơn 1
Ví dụ 5: Chứng minh rằng : 21
c
a
c
c
b
b
b
a
a
Giải:
Ta có : )1(
11
c
b
a
a
b
a
a
c
b
a
b
a
cbaba
Tương tự ta có : )2(
c
b
a
b
c
b
b
, )3(
c
b
a
c
c
a
c
Cộng vế theo vế các bất đẳng thức (1), (2), (3), ta được :
1
c
a
c
c
b
b
b
a
a (*)
Ta có : )4(
c
b
a
ca
b
a
a
baa
Tương tự : )5(
c
b
a
ba
c
b
b
, )6(
c
b
a
bc
a
c
c
Cộng vế theo vế các bất đẳng thức (4), (5), (6), ta được :
2
c
a
c
c
b
b
b
a
a (**)
Từ (*) và (**) , ta được : 21
c
a
c
c
b
b
b
a
a (đpcm)
Phương pháp 3: Dùng bất đẳng thức phụ
Kiến thức:
a) xyyx 2
22
b) xyyx 22 dấu( = ) khi x = y = 0





![Bài tập so sánh hơn và so sánh nhất của tính từ [kèm đáp án/mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250808/nhatlinhluong27@gmail.com/135x160/77671754900604.jpg)
![Tài liệu tham khảo Tiếng Anh lớp 8 [mới nhất/hay nhất/chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250806/anhvan.knndl.htc@gmail.com/135x160/54311754535084.jpg)




![Tài liệu Lý thuyết và Bài tập Tiếng Anh lớp 6 [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250802/hoihoangdang@gmail.com/135x160/18041754292798.jpg)




