
CÁC DẠNG BIỂU ĐỒ THỂ HIỆN SỰ
TƯƠNG QUAN CỦA DỮ LIỆU
1

•Với bộ dữ liệu có từ hai biến định lượng trở lên, ta có thể hình dung mối tương
quan của các biến thông qua hình ảnh trực quan từ các dạng:
•biểu đồ phân tán (scatter plots)
•biểu đồ bong bóng (bubble chart)
•ma trận phân tán (scatterplot matrix)
•biểu đồ tương quan (correlogram).
•Ngoài ra, khi bộ dữ liệu có số lượng biến quá nhiều, việc giảm kích thước thông
qua phân tích thành phần chính (PCA) được xem là phương pháp hữu hiệu.
Giới thiệu
2

1. Biểu đồ phân tán (scatter plots)
•Biểu đồ phân tán (scatter plots hay scatter diagram) là một loại biểu đồ sử
dụng tọa độ Descartes để hiển thị giá trị và mối quan hệ giữa hai biến định
lượng cho một tập dữ liệu.
•Dữ liệu được hiển thị dưới dạng tập hợp các điểm, mỗi điểm có giá trị của
một biến xác định vị trí trên trục hoành và giá trị của biến khác xác định vị trí
trên trục tung.
3
1. Biểu đồ phân
tán (scatter
plots)
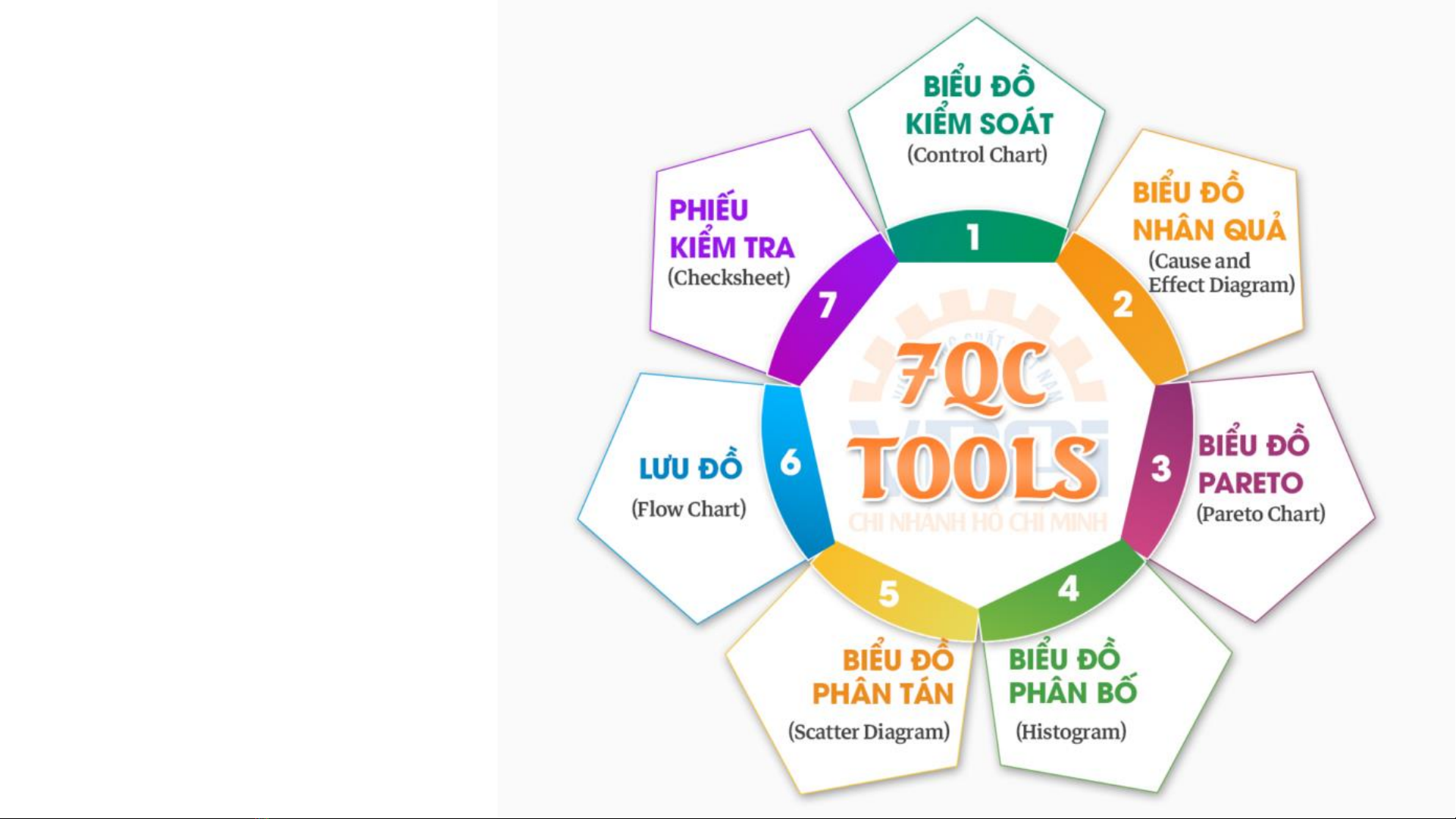
•Biểu đồ phân tán là một
trong 7 công cụ cơ bản
của kiểm soát chất
lượng trong doanh
nghiệp (Hình 1)
4
•Hình 1. 7 công cụ kiểm
soát chất lượng (Nguồn:
Viện Năng suất Việt
Nam - VNPI)

1. Biểu đồ phân tán (scatter plots)
•Biểu đồ phân tán có thể được dùng khi 2 biến định lượng độc lập hoặc có
một biến phụ thuộc vào biến còn lại.
•Trong trường hợp phụ thuộc, biến phụ thuộc (biến được dự đoán) thường
được vẽ dọc theo trục tung, biến độc lập (biến dùng để đưa ra dự đoán)
được vẽ dọc theo trục hoành.
•Trong trường hợp cả 2 biến độc lập với nhau, mỗi biến được vẽ ở một trục.
•Biểu đồ phân tán sẽ chỉ minh họa mức độ tương quan (không phải quan hệ
nhân quả) giữa hai biến.
5


























