CHƯƠNG 3: PHƯƠNG PHP PHN T HU HN
FINITE ELEMENT METHOD (FEM)
3.1. Khinim vê phương php PTHH
3.2. Nidung phương php PTHH –mô hnh chuynv
3.3. Rirchasơ đôtnh
3.4. Hmchuynv – hmdng
3.5. Xây dng phương trnh cân bng –Ma trnđô cng
phntư
3.6. Phpchuyntrctađô
3.7. Ghpniccphntư – thitlpma trnđô cng va
vectơ titrng ntcatonhê ktcu
e
K
1
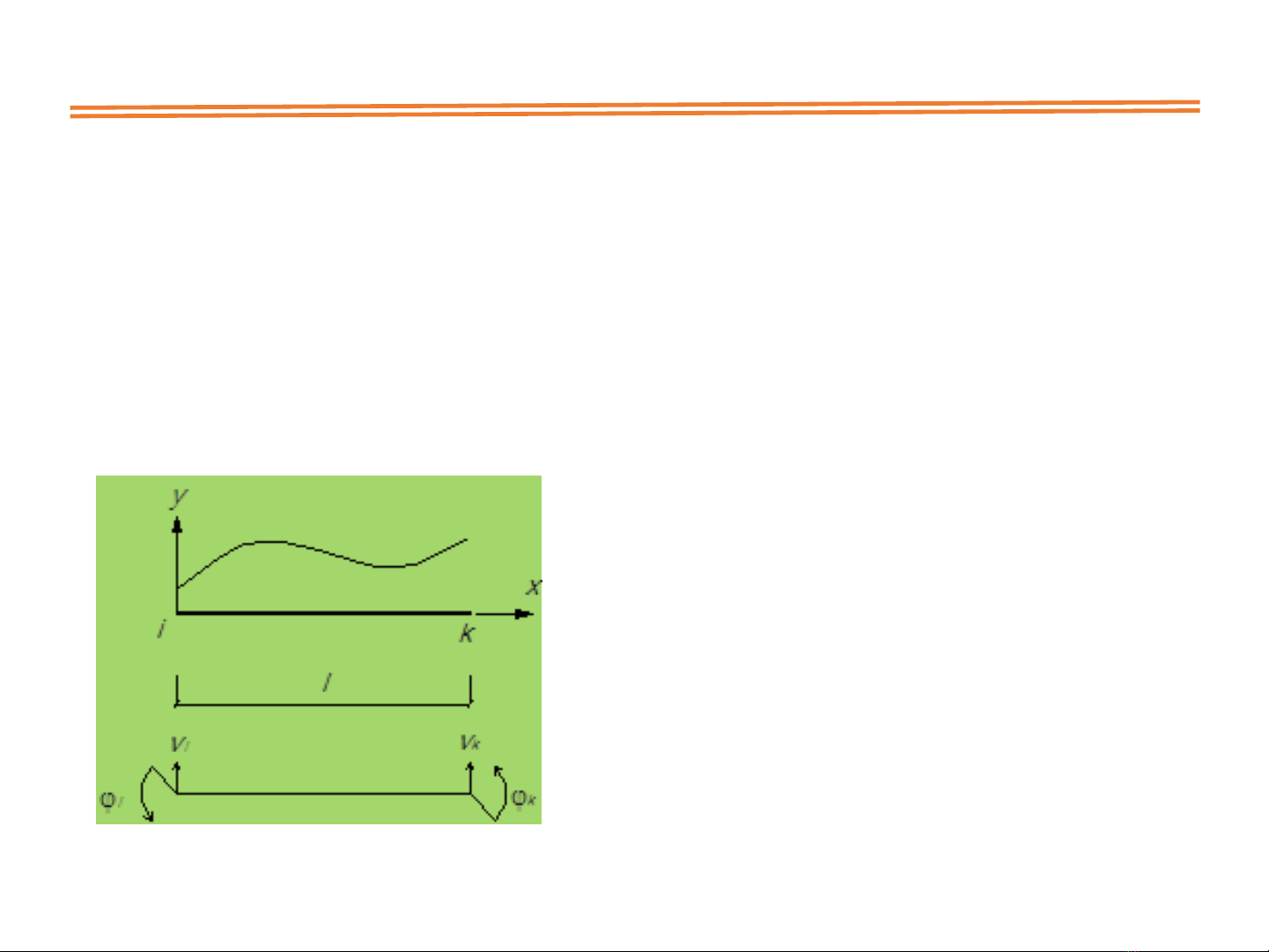
3.1. KHI NIỆM VỀ PP PHN T HU HN
Thcchtcaphương php PTHH l tmcch đưa vicgiicc
phương trnh vi phân đêtmnhm trên tonbôktcuvê vic
giiccphương trnh đisôđêtmcc giatr cahmtimtsô
đimnt.
(1) Đưa vicgiiPT vi phân (1)
đêtmhmvê vicgii
PT đisô(2) đêtm gia tr
cahm v vađohmca
n ticcnt :
(2)
,
(x) (x )
Z F v , v , x F(q)
i i k k
Z f v , , v , f (q)
(x)
v
i i k k
v , , v ,
2
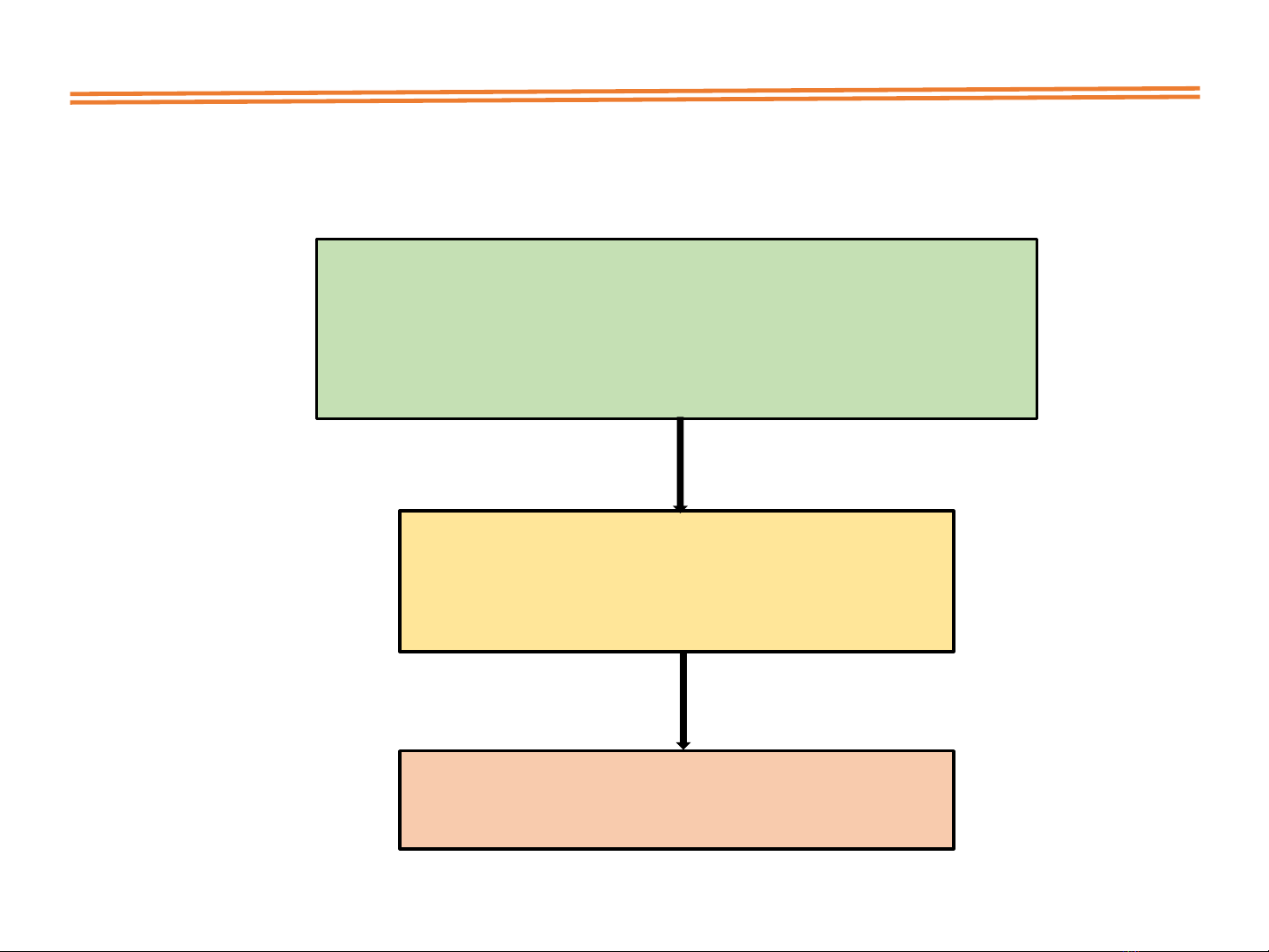
3.1. KHI NIỆM VỀ PP PHN T HU HN
Trnh tư gii
Rirchaktcu liên tcthnh ccphn
tưhuhn. Xcđnh cc thông sôđc
trưng va phương trnh gii cho tng phntư
Ghpniccphntưvohêta
đôchung. Giihê phương trnh
xcđnh chuynv tint
Xcđnh trng thitiv tr btky
trong ktcu
3
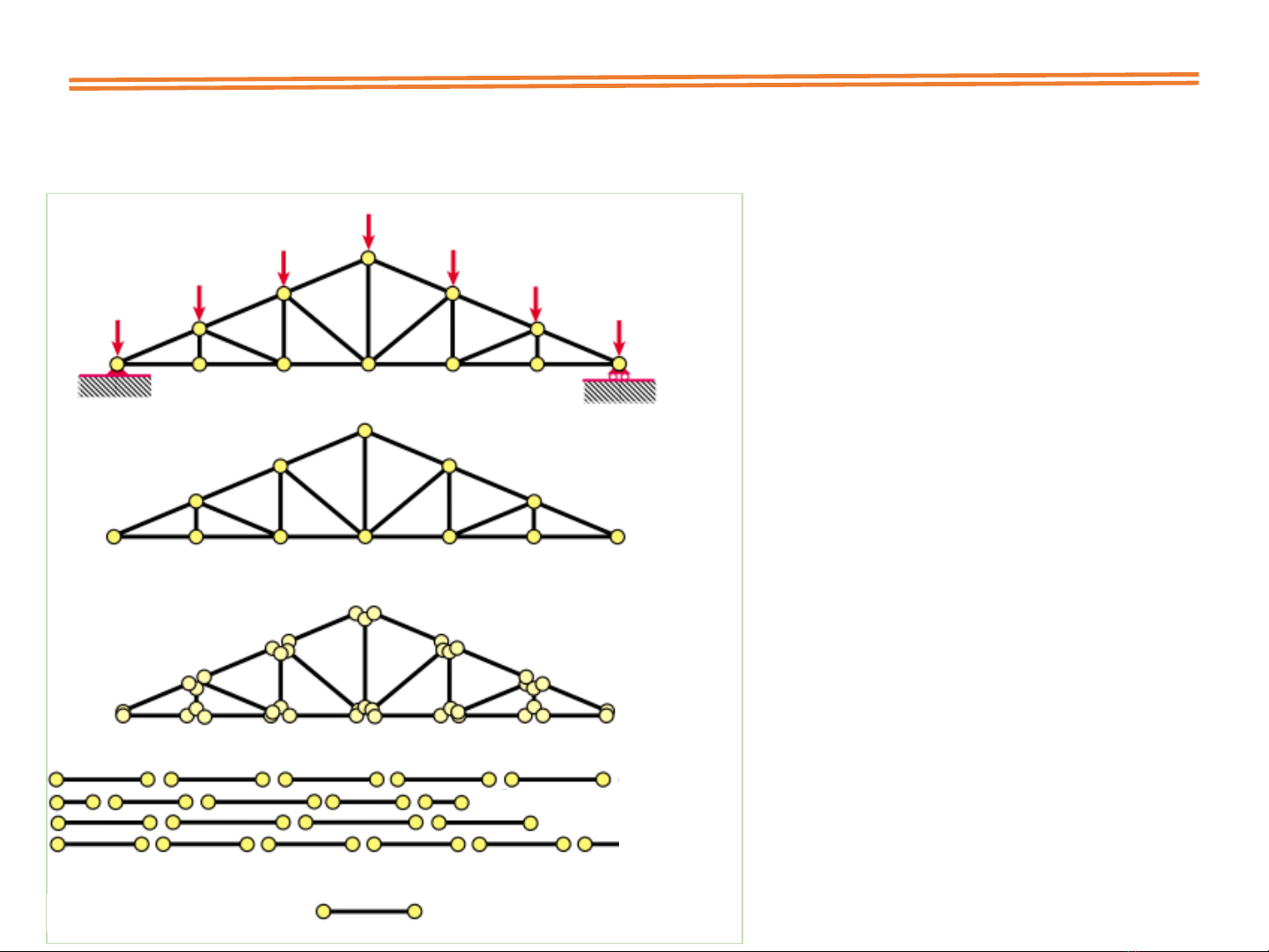
3.1. KHI NIỆM VỀ PP PHN T HU HN
Rirchahê thnh ccphntư
Mô Mô hnh PTHH
Loibocc liên kt
vatitrng
ThodiccPT
Đnh v,đưa vêhêta
đôriêng caPT
PT mu
4
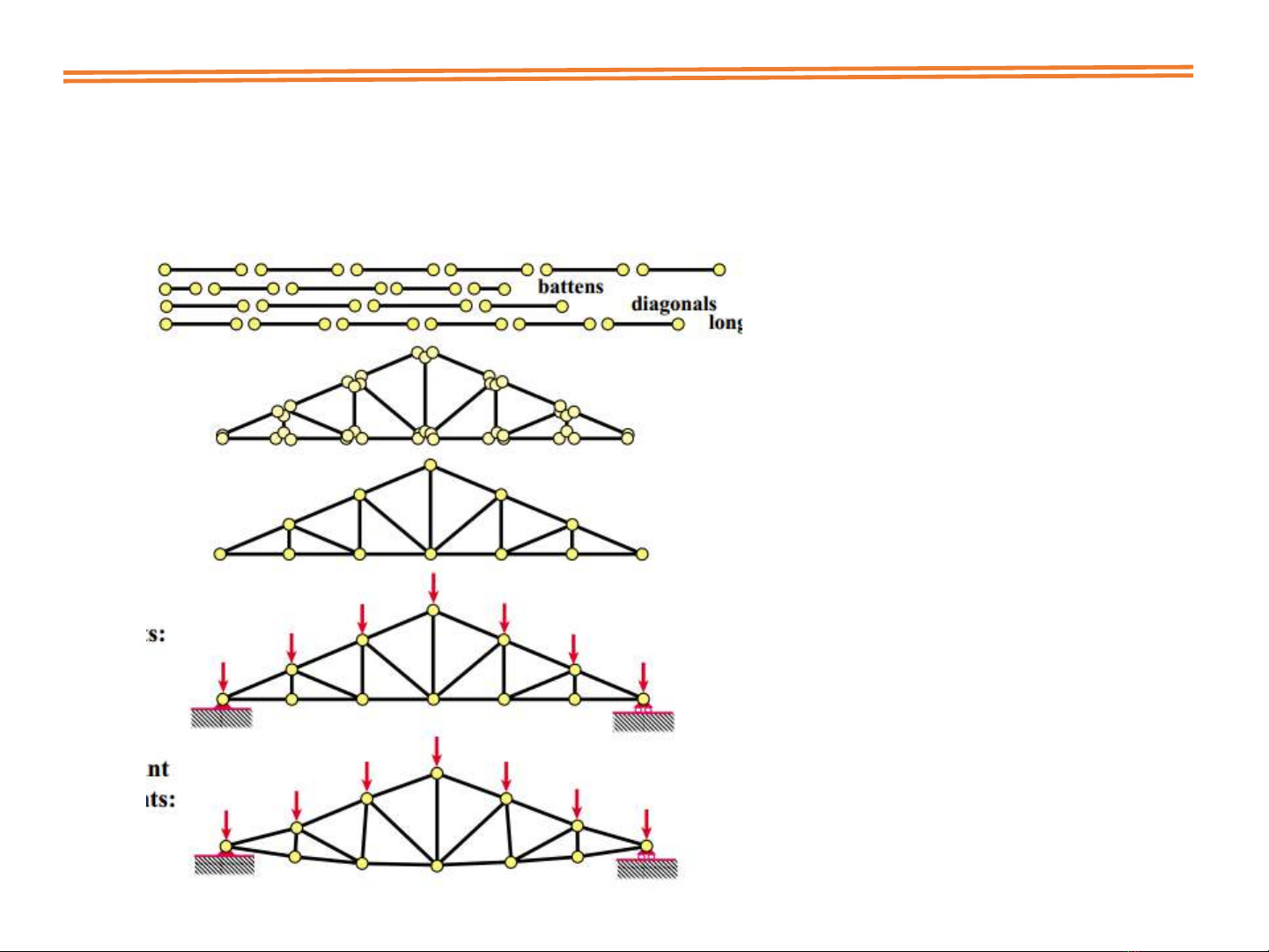
3.1. KHI NIỆM VỀ PP PHN T HU HN
Ghpniva gii
Dng PT
Đưa vêhêtađôchung
GhpniccPT vohê
Đttitrng valiên kt
Giihê phương trnh
xcđnh chuynv ti
nt
5