1
Chương 8.
PHƯƠNG PHÁP CHUYỂN VỊ VÀ CÁCH
TÍNH HỆ PHẲNG SIÊU ĐỘNG
Phương pháp lực: ẩn số là các lực.
Phương pháp chuyển vị: ẩn số là các chuyển vị.
Đôi khi còn gọi
là phương pháp biến dạng.
Bài 1. KHÁI NIỆM
1. Khái niệm
1.1
Các giả thiết
1.1.1 Nút tuyệt đối cứng: Khi đó các đầu thanh cùng chung
nút sẽ có những chuyển vị như nhau.
1.1.2 Đối với các thanh chịu uốn, ta bỏ qua ảnh hưởng của
biến dạng trượt so với biến dạng uốn.
1.1.3 Đối với các thanh chịu uốn, ta bỏ qua ảnh hưởng của
biến dạng đàn hồi dọc trục so với biến dạng uốn. Biến dạng
dọc trục vì nhiệt không được bỏ qua.
Từ giả thiết này và giả thiết chuyển vị của
hệ được xem là nhỏ
==>
Khoảng cách giữa hai nút ở 2 đầu thanh theo phương ban
đầu của cấu kiện là không thay đổi (trừ trường hợp nhiệt
và cấu
kiện có 2 đầu khới với độ cứng khác nhau vô cùng).
Phương pháp chuyển vị áp dụng thích hợp cho:
Dầm
Khung
2
Bài 1. KHÁI NIỆM
1. Khái niệm
1.1
Khái niệm về hệ xác định động và hệ siêu động
Có thể so sánh với định nghĩa hệ siêu tĩnh và hệ tĩnh định.
Hệ xác định động là hệ khi chịu chuyển vị cưỡng bức, t
a có thể
xác định được chuyển vị tại các nút theo các
điều kiện động học
(hình học).
Hệ siêu động là hệ khi chịu chuyển vị cưỡng bức,
nếu chỉ dùng
các điều kiện động học (hình học) thì không đủ để xác định tất
cả các chuyển vị tại các nút của hệ, mà cần bổ
sung thêm các
điều kiện cân bằng.
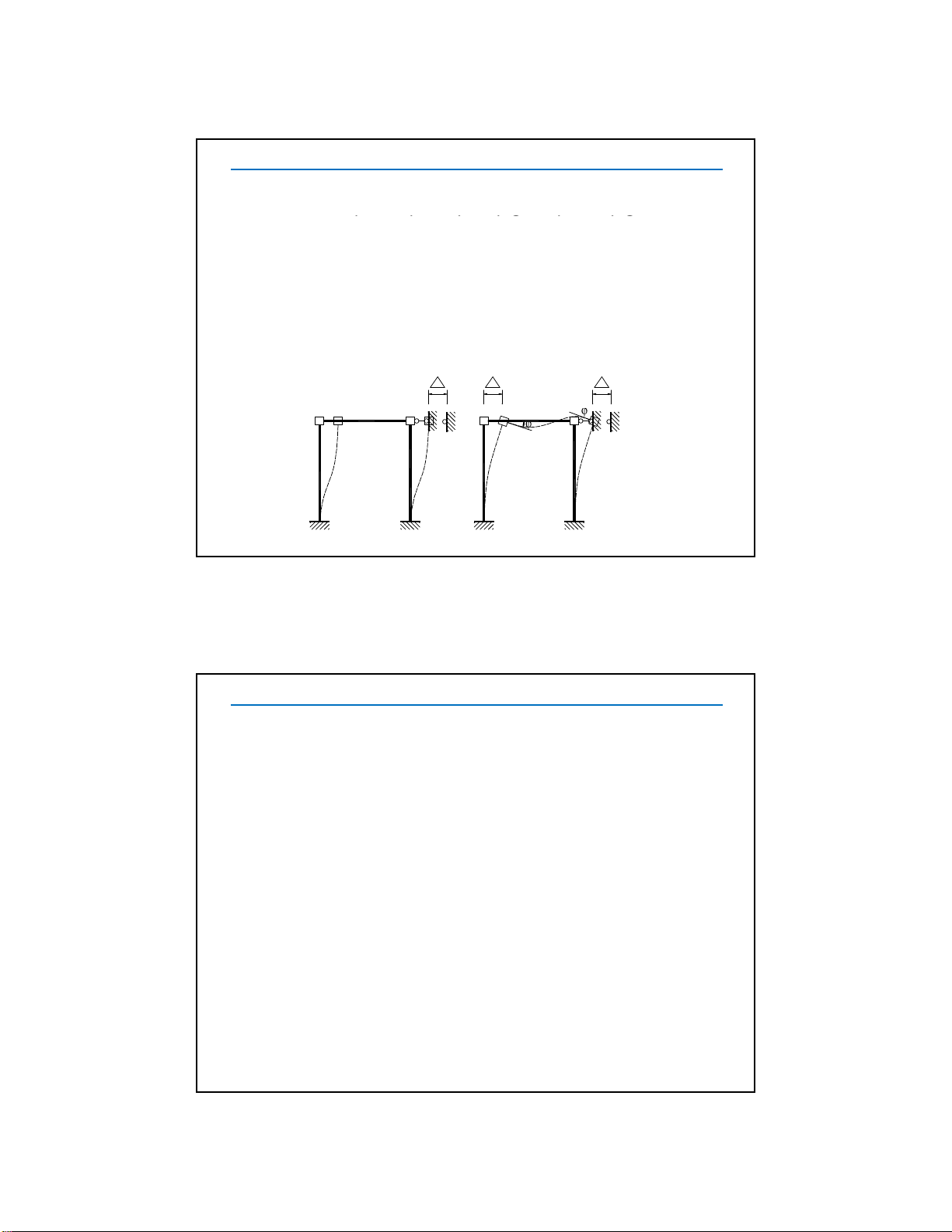
1.2. Khái niệm về hệ xác định động và hệ siêu động
A B A B
A
B
a) Hệ xác định động b) Hệ siêu động
Bài 1. KHÁI NIỆM
1. Khái niệm
1.3. Bậc siêu động
Bậc siêu động là số chuyển vị
độc lập chưa biết của các nút
trong hệ.
1 2
n n n
n
1
là số chuyển vị xoay độc lập của các nút (= số nút trong hệ).
n
2
là số chuyển vị thẳng độc lập của các nút.
3
Bài 2. CÁCH TÍNH HỆ SIÊU ĐỘNG
CHỊU TẢI TRỌNG BẤT ĐỘNG
1. Nội dung phương pháp chuyển vị
Tính trên hệ cơ bản (hệ thực + một số liên kết thêm vào).
Bổ sung vào hệ cơ bản các điều kiện để hệ cơ bản làm
việc giống hệ thực.
Bài 2. CÁCH TÍNH HỆ SIÊU ĐỘNG
CHỊU TẢI TRỌNG BẤT ĐỘNG
2. Hệ cơ bản của phương pháp chuyển vị
Là hệ suy ra từ hệ siêu động đã cho bằng cách đặt thêm vào hệ
những liên kết phụ nhằm ngăn cản chuyển vị xoay và chuyển vị
thẳng của các nút trong hệ.
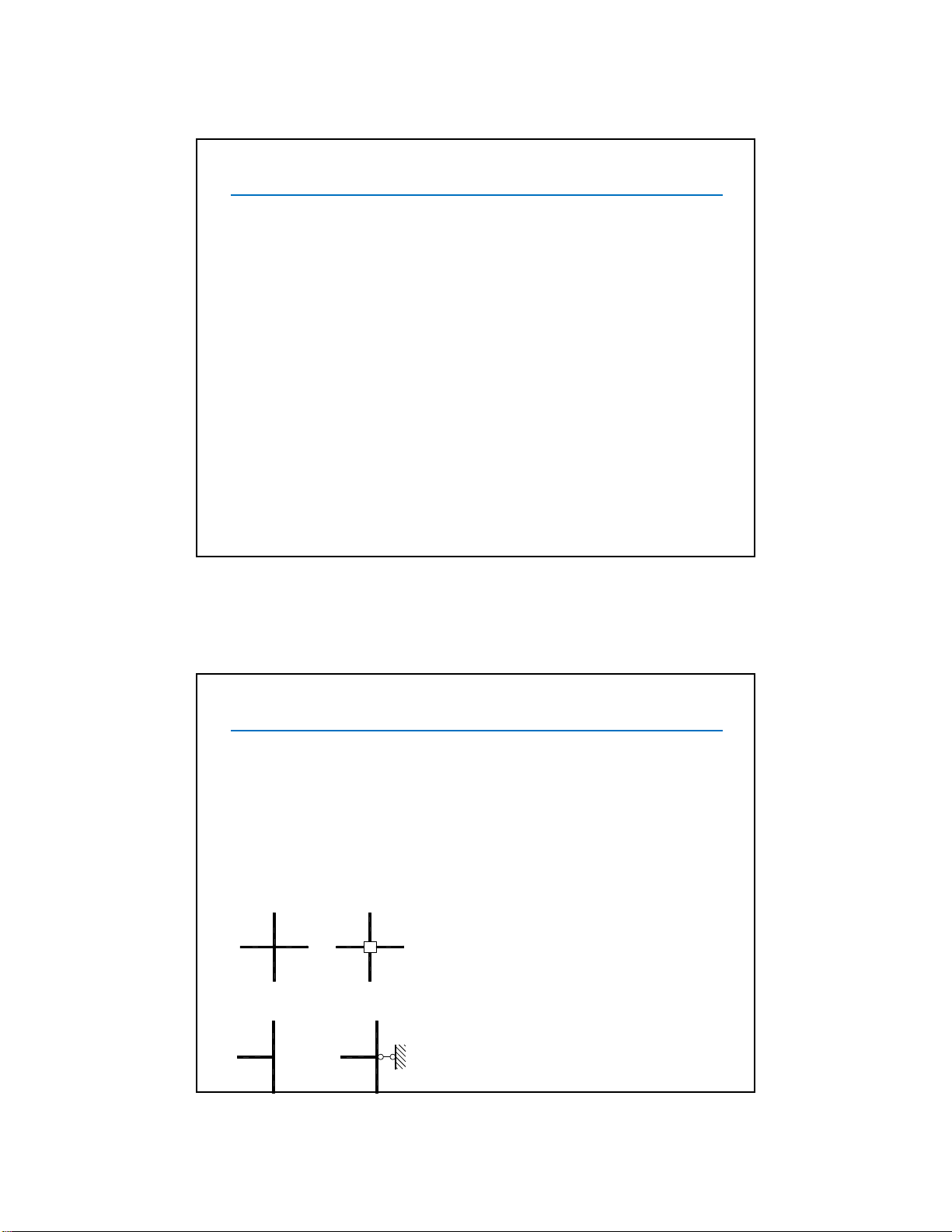
2 loại liên kết phụ:
Liên kết mômen: không xoay n
hưng vẫn có thể chuyển vị thẳng.
Ký hiệu:
Liên kết lực: ngăn cản chuyển vị thẳng. Ký hiệu:
4
Bài 2. CÁCH TÍNH HỆ SIÊU ĐỘNG
CHỊU TẢI TRỌNG BẤT ĐỘNG
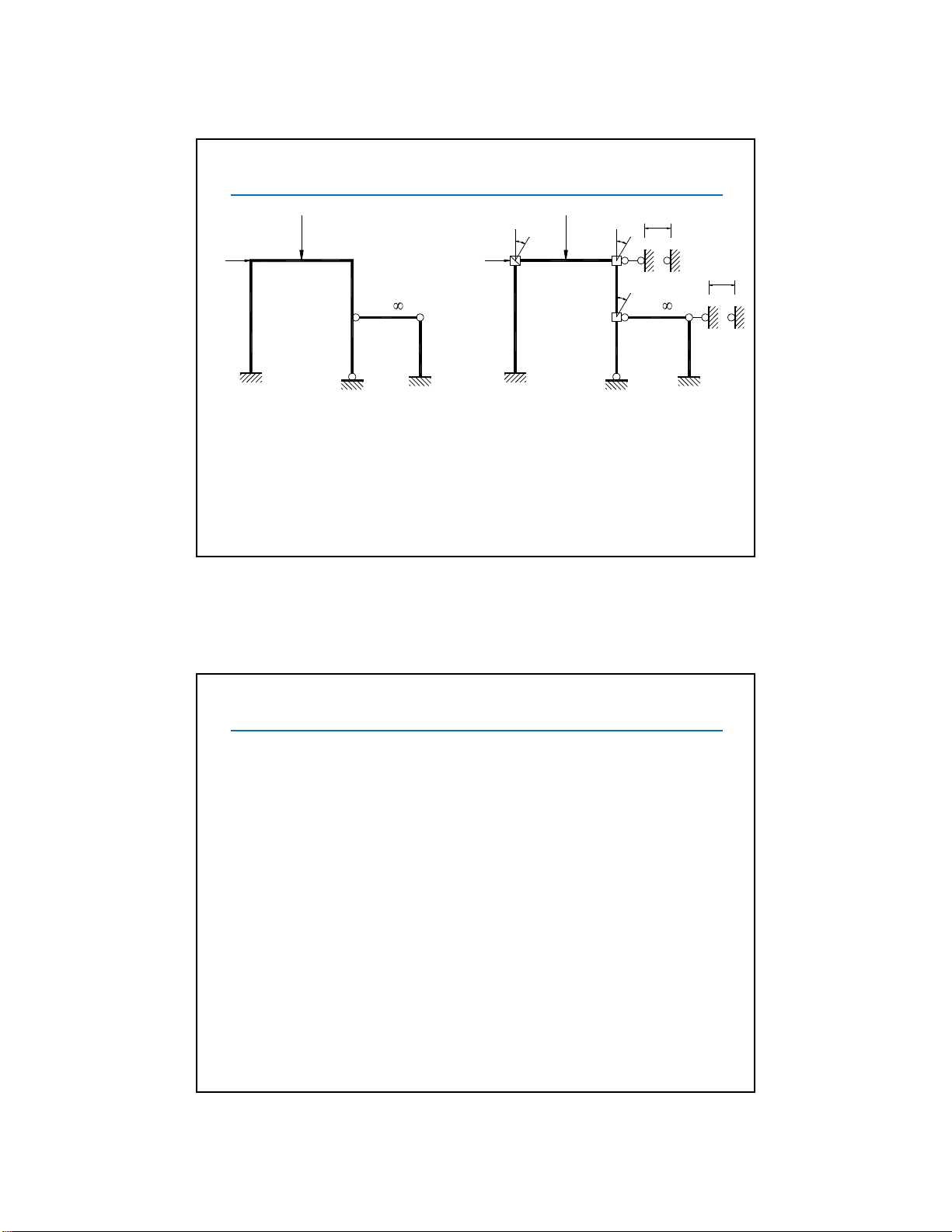
3. Ví dụ
B C
A
DE
FG
EI=const EA=
P
PB C
A
DE
FG
EI=const EA=
P
P
Z1Z2
Z4
Z3
Z5
Hệ cơ bản có thể là:
+ hệ xác định động: nếu số liên kết thêm vào bằng
số bậc siêu
động.
+
hệ siêu động (bậc thấp hơn): nếu số liên kết thêm vào bằng số
bậc siêu động.
Quan trọng: Trong h
ệ cơ bản chỉ tồn tại những cấu kiện mẫu đã
được nghiên cứu trước thì: hệ cơ bản xác định động, hệ duy thất.
Bài 2. CÁCH TÍNH HỆ SIÊU ĐỘNG
CHỊU TẢI TRỌNG BẤT ĐỘNG
4. Hệ phương trình chính tắc của phương pháp chuyển vị
Để hệ cơ bản làm việc giống hệ thực ta cần thêm vào hệ cơ bản
những chuyển vị cưỡng bức (Z
1
, Z
2
, …, Z
n
) tại các liên kết đặt
thêm vào hệ.
Điều kiện:
1 2
( , ,..., , )
0
n
k Z Z Z P
R
1 2
... 0
n
kZ kZ kZ kP
R R R R
Trong đó:
i
kZ
R
là phản lực tại
liên kết thứ k trong hệ cơ bản, do
chuyển vị cưỡng bức tại liên kết thứ i gây ra.
kP
R
là phản lực tại liên kết thứ k trong hệ cơ bản, do
tải
trọng gây ra trong hệ cơ bản.
5
Bài 2. CÁCH TÍNH HỆ SIÊU ĐỘNG
CHỊU TẢI TRỌNG BẤT ĐỘNG
4. Hệ phương trình chính tắc của phương pháp chuyển vị
Nếu gọi
ki
r
là phản lực tại
liên kết thứ k do chuyển vị cưỡng bức
do riêng Z
i
=1 tại liên kết thứ i gây ra trên hệ cơ bản, thì:
i
kZ ki i
R r Z
Phương trình trên được viết lại:
1 1 2 2
... 0
k k kn n kP
r Z r Z r Z R
với k=1,2,…,n.
Hay:
11 1 12 2 1 1
21 1 22 2 2 2
1 1 2 2
... 0
... 0
... 0
n n P
n n P
n n nn n nP
r Z r Z r Z R
r Z r Z r Z R
r Z r Z r Z R
Lưu ý:
Quy ước chiều dương của phản lực
ki
r
cùng chiều với
chiều dương của các chuyển vị cưỡng bức.
ki ik
r r
Bài 2. CÁCH TÍNH HỆ SIÊU ĐỘNG
CHỊU TẢI TRỌNG BẤT ĐỘNG
5. Cách xác định nội lực trong hệ cơ bản xác định động
5.1. Biểu đồ nội lực do tải trọng gây ra trong hệ cơ bản
o
P
M
Tải trọng chỉ gây ra ảnh hưởng cục bộ trong từng phần tử.
Sử dụng bảng phần tử mẫu.
5.2. Biểu đồ nội lực do chuyển vị cưỡng bức bằng đơn
vị gây ra trong hệ cơ bản
Sử dụng bảng phần tử mẫu.
5.3. Cách xác định các hệ số và số hạng tự do trong
Liên kết mômen
Tính
ki
r
: Tách nút trên biểu đồ
i
M
, cân bằng.
Tính
kP
R
: Tách nút trên biểu đồ
o
P
M
, cân bằng.
Liên kết lực
Cắt vòng qua liên kết k