GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bôSlide 708
Chương 10
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bôSlide 709
Động lượng, Mômen động lượng, Động năng
k
m
4
m
n
m
2
m
m
5
m
1
m
k
F
k
v
O
k
r
k k
m v
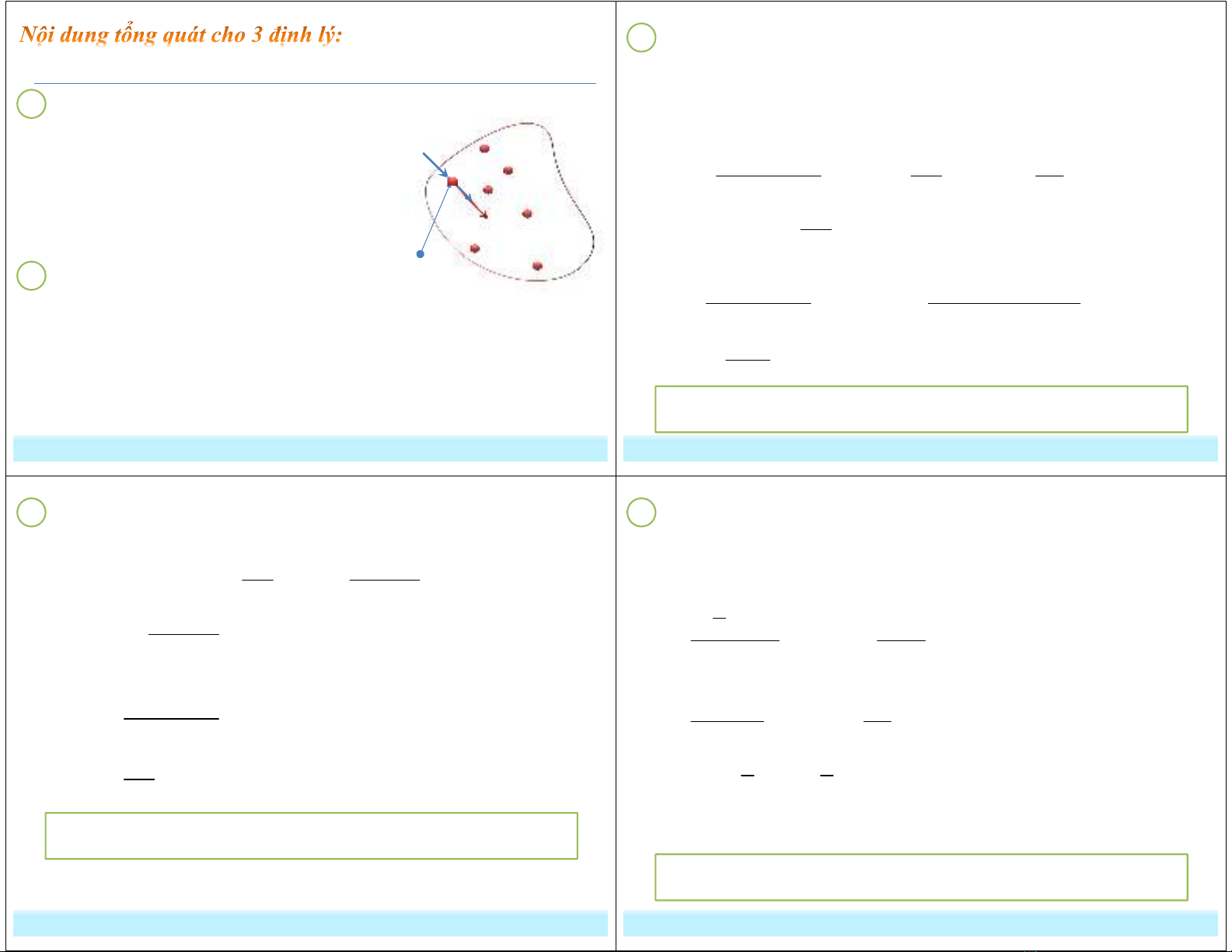
1 Hai đặc trưng của hệ lực trên hệ chất điểm
* Véc tơ lực chính
1
n
k
k
R F
=
=
∑
* Véc tơ mômen lực chính đối với O
1 1
( ) ( )
n n
O k k
O k
k k
M m F r F
= =
= = ∧
∑ ∑

2 Hai đặc trưng động học của hệ chất điểm
* Véc tơ động lượng chính
1
( )
n
k k
k
Q m v
=
=
∑
* Véc tơ mômen động lượng chính đối với O
1 1
( ) ( )
n n
O
O k k k k k
k k
K m m v r m v
= =
= = ∧
∑ ∑
Cố định
Chất điểm k bất kỳ
- Xác định bởi với O là điểm tùy chọn
- Khối lượng
- Chịu lực tác dụng
k
r
k
m
k
F
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bô Slide 711
4 Mối quan hệ giữa véc tơ mômen lực chính với véc tơ mômen
động lượng chính đối với cùng một điểm– Định lý Mômen
động lượng
( )
k k k
k k k k k k k k k O
m a F r m a r F r m a m F
=
⇒
∧ = ∧
⇒
∧ =
Từ:
Trong một hệ chất điểm, đạo hàm bậc nhất theo thời gian của véc tơ mômen
động lượng chính tại điểm nào thì bằng véc tơ mômen lực chính tại điểm đó.
( )
( ) ( )
( ) (0) ( )
k k k k k
k k k k
k
k k k k k
d r m v dv dr
r m m v
dt dt dt
dv
r m r m a
dt
∧
= ∧ + ∧
= ∧ + = ∧
mà:
1
1
( )
( )
( ) ( )
n
k k k n
k
k k k
k k
O O
k
d r m v
d r m v
m F m F
dt dt
=
=
∧
∧
=⇒=
∑∑
Từ:
O
O
d K
M
dt
=

Do đó:
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bô Slide 710
3 Mối quan hệ giữa véc tơ lực chính với véc tơ động lượng chính
– Định lý Động lượng
1 1
1
1
( )
( )
( )
k k k
k k k
k k k
n n
k k k
k k
n
k k n
kk
k
dv d m v
m a F m F F
dt dt
d m v F
dt
d m v
F
dt
dQ R
dt
= =
=
=
=⇒=⇒=
⇒=
⇒=
⇒=
∑ ∑
∑∑
Từ:
Trong một hệ chất điểm, đạo hàm bậc nhất theo thời gian của véc tơ động
lượng chính thì bằng véc tơ lực chính.
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bô Slide 712
5 Mối quan hệ giữa công suất của hệ lực với động năng của hệ
chất điểm
2
1
1
. .
1
( ) ( )
2.
( )
k k
k k k k k k
k k k
k
k k
n
kn
k
k
k
m a F m a v F v
d m v d T
F v W
dt dt
d T dT
W W
dt dt
=
=
=⇒=
⇒=⇒=
⇒=⇒=
∑∑
Từ:
Trong một hệ chất điểm, đạo hàm bậc nhất theo thời gian của tổng động năng
của hệ thì bằng tổng công suất của lực trong hệ.
2 2
1 1
2 2
k k k k k
T m v m v
= =
: động năng của chất điểm thứ k
k
k k
W F v
=
: công suất của lực
k
F
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bôSlide 713
6 Lưu ý áp dụng định lý cho hệ vật rắn
Khi áp dụng định lý cho vật rắn thì cần lưu ý những điều sau:
1
0
n
i i
k
k
R F
e i e
R R R R R
=
= =
∑
= + → =
1
( ) 0
n
i i
O k
O
k
M m F
e i e
O O O O O
M M M M M
=
= =
∑
= + → =

    
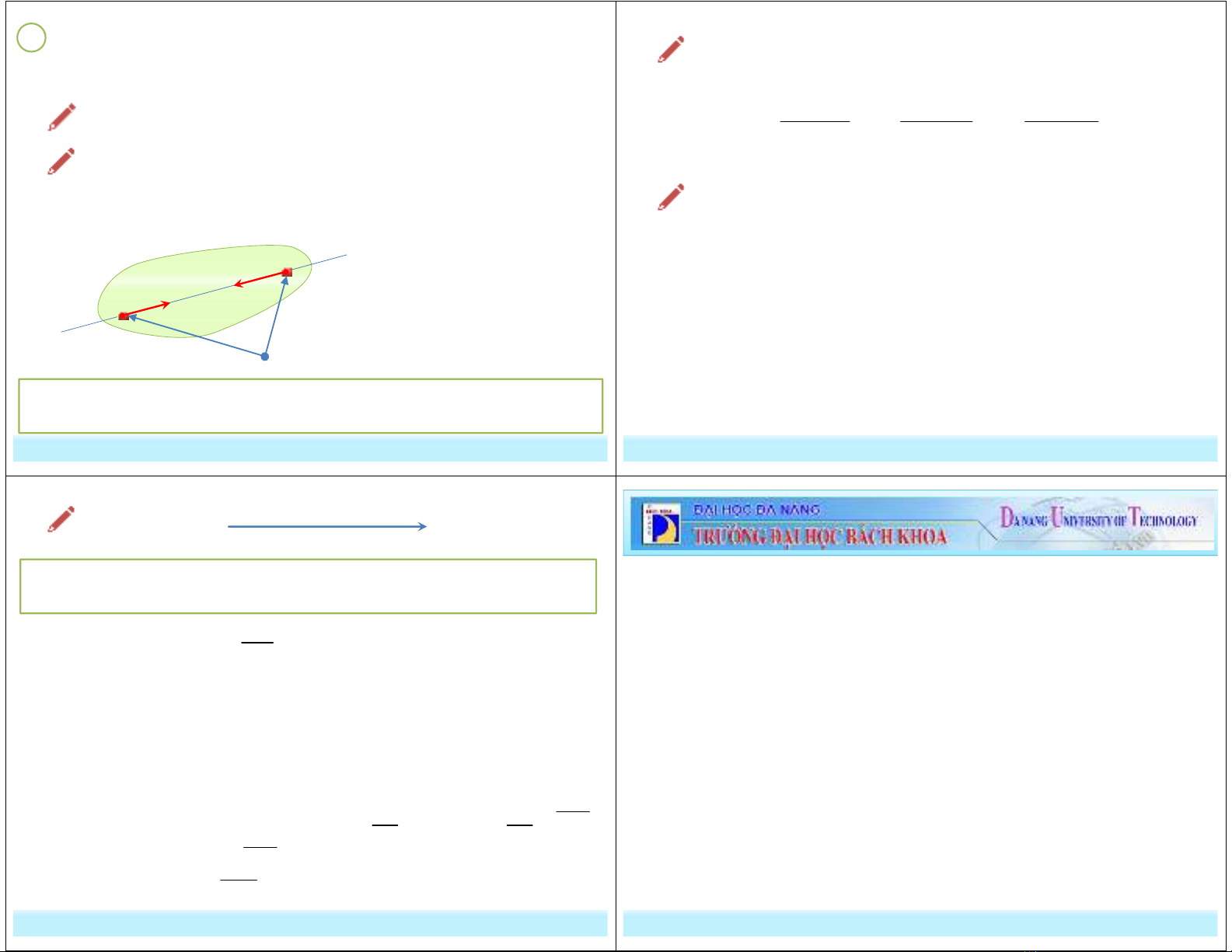
Thật vậy, xét hai chất điểm bất kỳ M và N trong cùng một vật rắn,
chúng tương tác nhau bởi các nội lực như hình vẽ.
M
N
O
M
r
N
r
i
MN
F
i
NM
F
i i i
NM MN
F F F
= =
Véc tơ lực chính và mômen lực chính do nội lực là bằng 0, nên nội lực
không làm phát sinh động lượng và mômen động lượng trong hệ.
0
i i
MN NM
F F
+ =
0
i i
MN NM
M N
r F r F
∧ + ∧ =
Rõ ràng:
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bôSlide 715
Các chất điểm về vị trí và động học liên hệ theo công thức sau:
1 1 1
. . .
, ,
n n n
k k k k k k
k k k
C C C
m r m v m a
r v a
M M M
= = =
= = =
∑ ∑ ∑
Mỗi định lý thể hiện nội dung định lý dưới những dạng công
thức khác nhau. Các bài sau, mỗi bài trình bày mỗi định lý.
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bôSlide 714
e i
W W W
= +
Vật rắn tuyệt đối
e
W W
=
0
i
W
=
Nội lực trong vật rắn biến dạng có sinh công, trong vật tuyệt đối cứng
không sinh công.
( ) . . . .
( ) . ( )
,
. ( )
i i i i
iMN NM MN MN
M N M N
i i i
MN MN
i i
MN
M
N
N
M
NM
dA F dr F dr F dr F dr
F dr dr F d NM
F
d NM
F
F
= + = −
= − = = −


Ta có:
Có thể biểu diễn (
α
là hằng số nào đó)
2
.
i
NM
F NM
α
=

2 2
2 2 2
( ) . . ( ) ( ) ( )
2 2
,
i i
MN NM
i
dA NM d NMF
d d MN
FNM
α α
α
= − = − = −
 

Do đó:
+Vật rắn biến dạng, có thể thay đổi nên nội lực sinh công
MN
+Vật rắn tuyệt đối cứng, không đổi nên nội lực không sinh công
MN
Công suất do nội lực:
i
i
dA
W
dt
=
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bôSlide 716
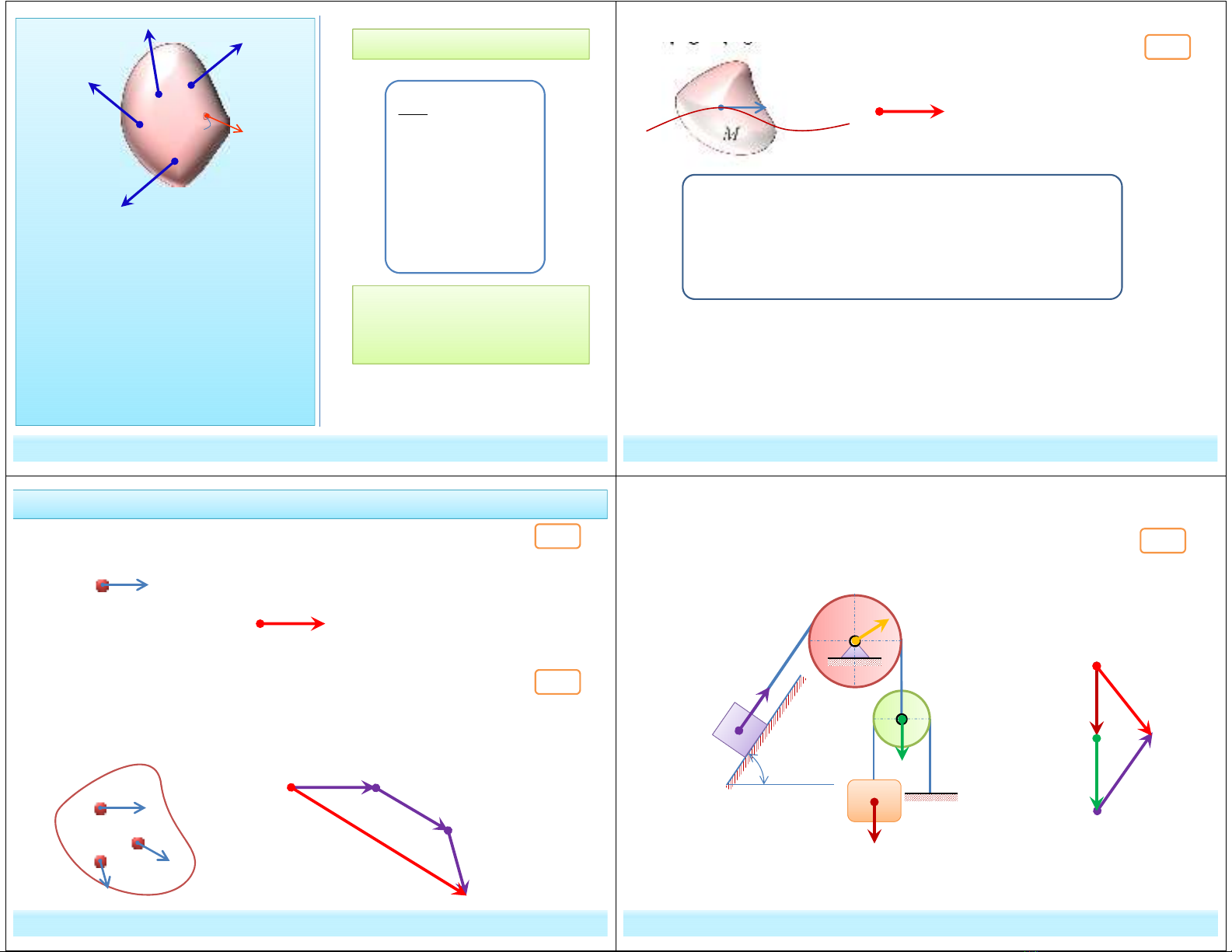
§1. Định lý động lượng
Trong phần này sẽ khảo sát mối quan hệ giữa động lượng của hệ
với véc tơ chính của ngoại lực tác dụng trên hệ.
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bôSlide 717
k
m
k
v
k
1
F
2
F
3
F
n
F
.
k k
k
Q m v
=
∑
...
e
dQ
R
dt
=
i
e e
dQ R dt d S
= =
i
1 2
2 1
e
Q Q S
−
− =
i
Véc tơ động lượng của hệ:
Véc tơ lực chính của hệ ngoại lực:
e
i
i
R F
=
∑
Một vài kết quả từ định lý
Nội dung định lý này được
làm rõ chi tiết trong phần
tiếp sau.
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bôSlide 719
c. Động lượng của vật rắn:
.
C
Q M v
=
M
C
C
v
.
C
Q M v
=
10.3
* Chứng minh:
k k k k
Q m v m r
= =
∑ ∑
ɺ
Mà:
k k C
m r Mr
=
∑
nên
C C
Q Mr Mv
= =
ɺ
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bôSlide 718
a. Động lượng của một chất điểm:
.
Q m v
=
m
v
b. Động lượng của hệ chất điểm:
2
m
1
m
n
m
1
v
2
v
n
v
1 1
1
.
Q m v
=
2 2
2
.
Q m v
=
.
n n
n
Q m v
=
Q
1. Động lượng
10.1
.
Q m v
=
1
n
k k
k
Q m v
=
=
∑
10.2
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bô Slide 720
d. Động lượng của hệ vật rắn:
α
1 2
1 2
. . ... .
n
C C n C
Q M v M v M v
= + + +
1
C
v
2
C
v
4
C
v
3
0
C
v
=
1
C
2
C
3
C
4
C
1
M
2
M
3
M
4
M
2
2
.
C
M v
Q
1
1
.
C
M v
4
4
.
C
M v
10.4
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bô Slide 721
Trong hệ trục tọa độ Descartes cố định thì:
1 2
1 2
1 2
1 2
2 2 2
1 2
1 2
. . ... .
. . ... .
. . ... .
n
n
n
x C C n C
y C C n C x y z
z C C n C
Q M x M x M x
Q M y M y M y Q Q Q Q
Q M z M z M z
= + + +
= + + + ⇒= + +
= + + +
ɺ ɺ ɺ
ɺ ɺ ɺ
ɺ ɺ ɺ
* Khi các véc tơ đã xác định, thì:
( 1, )
k
C
v k n
=
1
2 2 2
1
1
.
.
.
k
k
k
n
x k xC
k
n
y k yC x y z
k
n
z k zC
k
Q M v
Q M v Q Q Q Q
Q M v
=
=
=
=
=⇒= + +
=
∑
∑
∑
* Khi biết phương trình chuyển động của , thì:
( 1, )
k
C k n
=
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bô Slide 723
3. Định lý động lượng
a. Dạng động học:
1
n
e
k
k
dQ
F
dt
=
=
∑
10.7
* Chứng minh:
0
e i e
k
k k k
k k k
e e
k k
k k
dv
m a F F m F
dt
d dQ
m v F F
dt dt
= + ⇔ = +
⇔ = ⇔ =
∑ ∑ ∑ ∑ ∑
∑ ∑ ∑
Ta có:
10.8
b. Phương trình vi phân của chuyển động khối tâm:
1 1
n n
e e
k k
C C
k k
Ma F Mr F
= =
=⇒=
∑ ∑
ɺɺ
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bô Slide 722
2. Lực tác dụng
a. Véc tơ chính của ngoại lực
1
n
e e
k
k
R F
=
=
∑
b. Xung lượng của lực: biểu thị tác dụng của lực theo thời gian
+ Xung lượng nguyên tố: biểu thị tác dụng của lực trong dt
d S Fdt
=
+ Xung lượng hữu hạn: biểu thị tác dụng của lực từ t1 đến t2
2 2
1 1
1 2
t t
t t
S d S Fdt
−= =
∫ ∫
F const
=

Nếu thì
1 2
2 1
( )
S F t t
−
= −
10.6
10.5
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bô Slide 724
- Đối với hệ một vật rắn khối lượng M, khối tâm C:
1
1
1
.
.
.
n
e
xC k
k
n
e
yC k
k
n
e
zC k
k
M a X
M a Y
M a Z
=
=
=
=
=
=
∑
∑
∑
10.9a
(
)
(
)
(
)
, , , , , , ,
e
e e e e e e
k
C xC yC zC kx ky kx k k k
a a a a F F F F X Y Z
= = =
Lưu ý:
- Đối với hệ p vật rắn; vật rắn thứ k có khối lượng Mk, khối tâm Ck:
1 1
1 1
1 1
.
.
.
k
k
k
pn
e
k xC k
k k
pn
e
k yC k
k k
pn
e
k zC k
k k
M a X
M a Y
M a Z
= =
= =
= =
=
=
=
∑ ∑
∑ ∑
∑ ∑
10.9b