Bài giảng Cơ học Lý thuyết - Tuần 4 3/21/2011
Giảng viên Nguyễn Duy Khương 1
CHƯƠNG 4 Ma sát
2. Bài toán cân bằng có kể đến ma sát
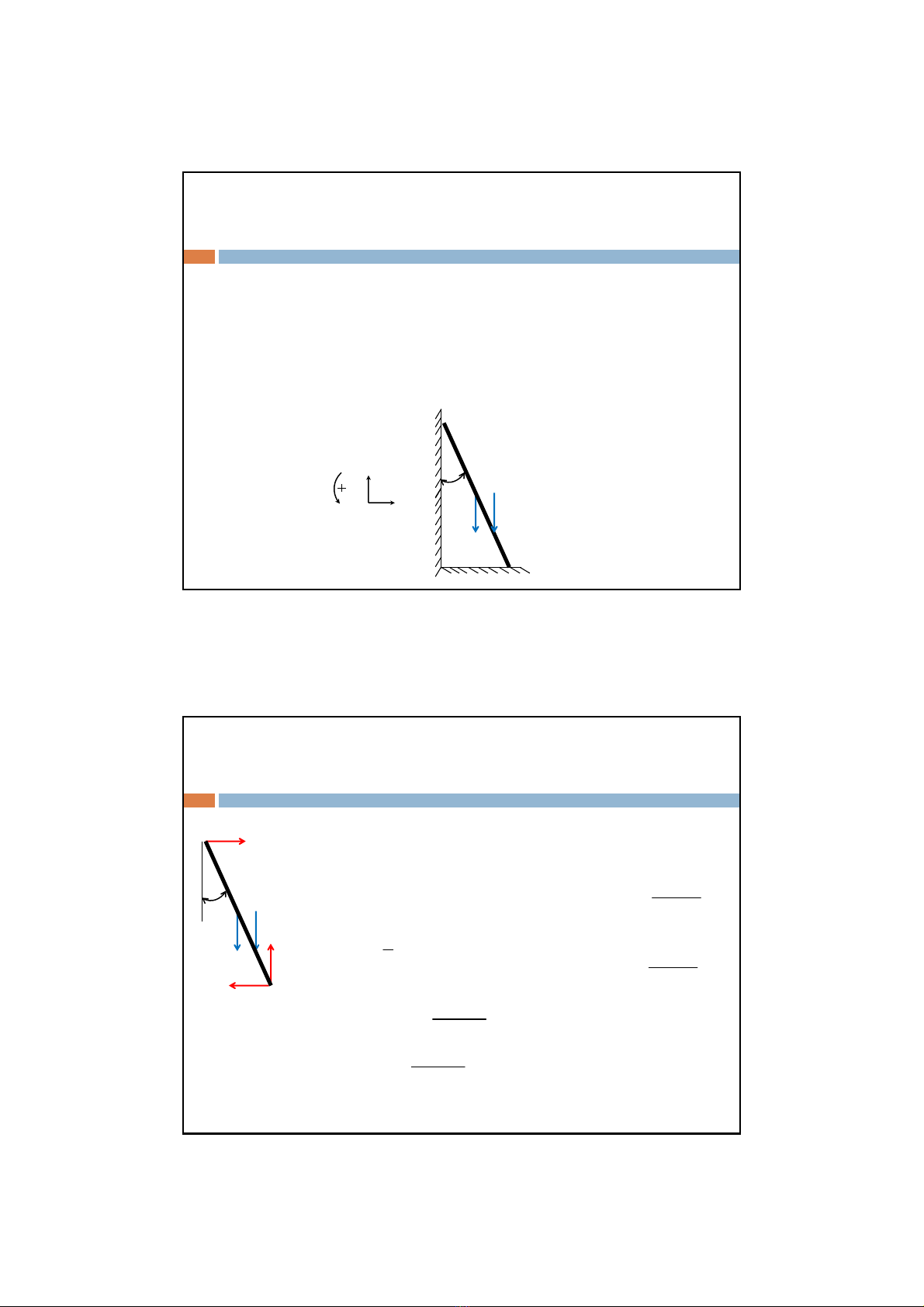
Ví dụ:Cho hệnhưhình vẽ, AB=l, dựng vào tường nghiêng so với
phương đứng mộtgóc,biếtcầu thang AB có trọng lượng Q tại
giữacầu thang và ngườiđứng trên cầu thang có trọng lượng P.
Hỏi góc bằng bao nhiêu để ngườiđitừdướichâncầu thang lên
đếnđỉnh mà thang vẫnkotrượt trong hai trường hợpsau
1. Ma sát tại A không đáng kểvà hệsốma sát trượttĩnh tạiBlàf
2. Ma sát trượttĩnh tạiAvàBđềubằng f
y
x
A
P
B
Q
CHƯƠNG 4 Ma sát
2. Bài toán cân bằng có kể đến ma sát
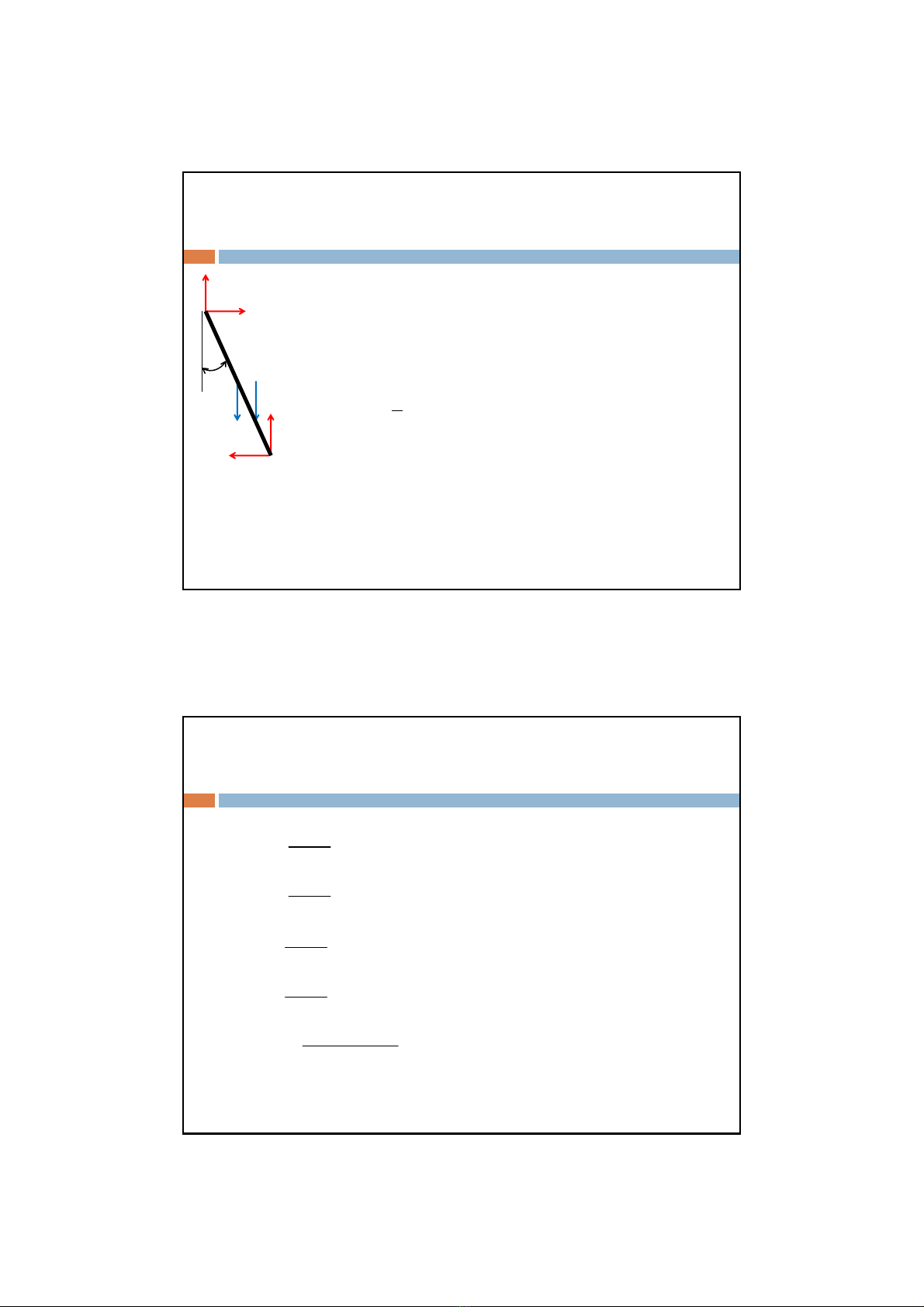
1. Ma sát tại A không đáng kểvà hệsốma sát trượttĩnh tạiBlàf
P
QNB
FB
NA
Nhậnxéttathấynếungườiđứng ởphía trên cao thì thang
có khảnăng trượt nhiềunhất nên cho P tác động tạiđiểmA
0
0
sin sin cos 0
2
Ax
B
A
y
B
B
F
FPQ
l
MQ P
NF
N
llN




2tan
2
2tan
2
A
B
B
N
N
F
QP
PQ
QP

Điềukiệnđể thang chưatrượttạiB
BB
FfN 2tan ( )
2
QP
f
PQ

tan 2 2
PQ
fPQ

B
A
Bài giảng Cơ học Lý thuyết - Tuần 4 3/21/2011
Giảng viên Nguyễn Duy Khương 2
CHƯƠNG 4 Ma sát
2. Bài toán cân bằng có kể đến ma sát
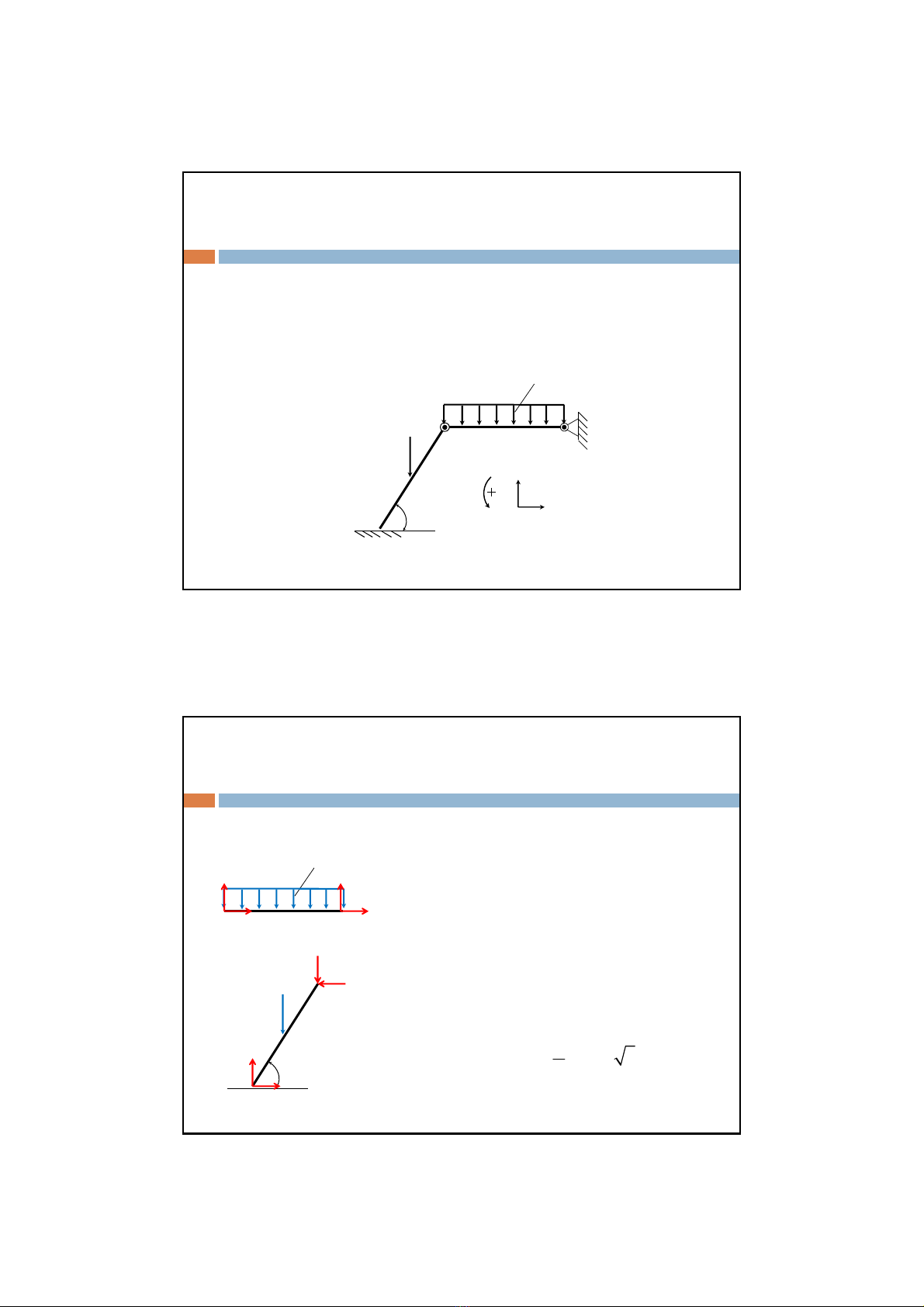
2. Ma sát trượttĩnh tạiAvàBđềubằng f
P
Q
Nhậnxéttathấynếungườiđứng ởphía trên cao thì thang
có khảnăng trượt nhiềunhất nên cho P tác động tạiđiểmA
0
0
sin sin cos sin 0
2
AB
BA
AA
x
y
B
F
FPQ
NF
NF
NF
l
MQ Pl l l




NB
FB
NA
FA
Vớiđiềukiện thang không trượt thì thang sẽkhông trượttại
A và B nên lựcmasáttạiAvàBgiớihạnlà:
BB
F
f
N
AA
F
f
N
Lập thành 5 phương trình 5 ẩn(NA,NB,FA,FB,)
B
A
CHƯƠNG 4 Ma sát
2. Bài toán cân bằng có kể đến ma sát
2
2
2
2
2
2
()
1
1()
1
()
1
()
1
2
tan ( )
2
A
B
A
B
fPQ
f
PQ
f
fPQ
f
fPQ
f
fPQ
P
N
N
F
QfQ
F






Bài giảng Cơ học Lý thuyết - Tuần 4 3/21/2011
Giảng viên Nguyễn Duy Khương 3
CHƯƠNG 4 Ma sát
2. Bài toán cân bằng có kể đến ma sát
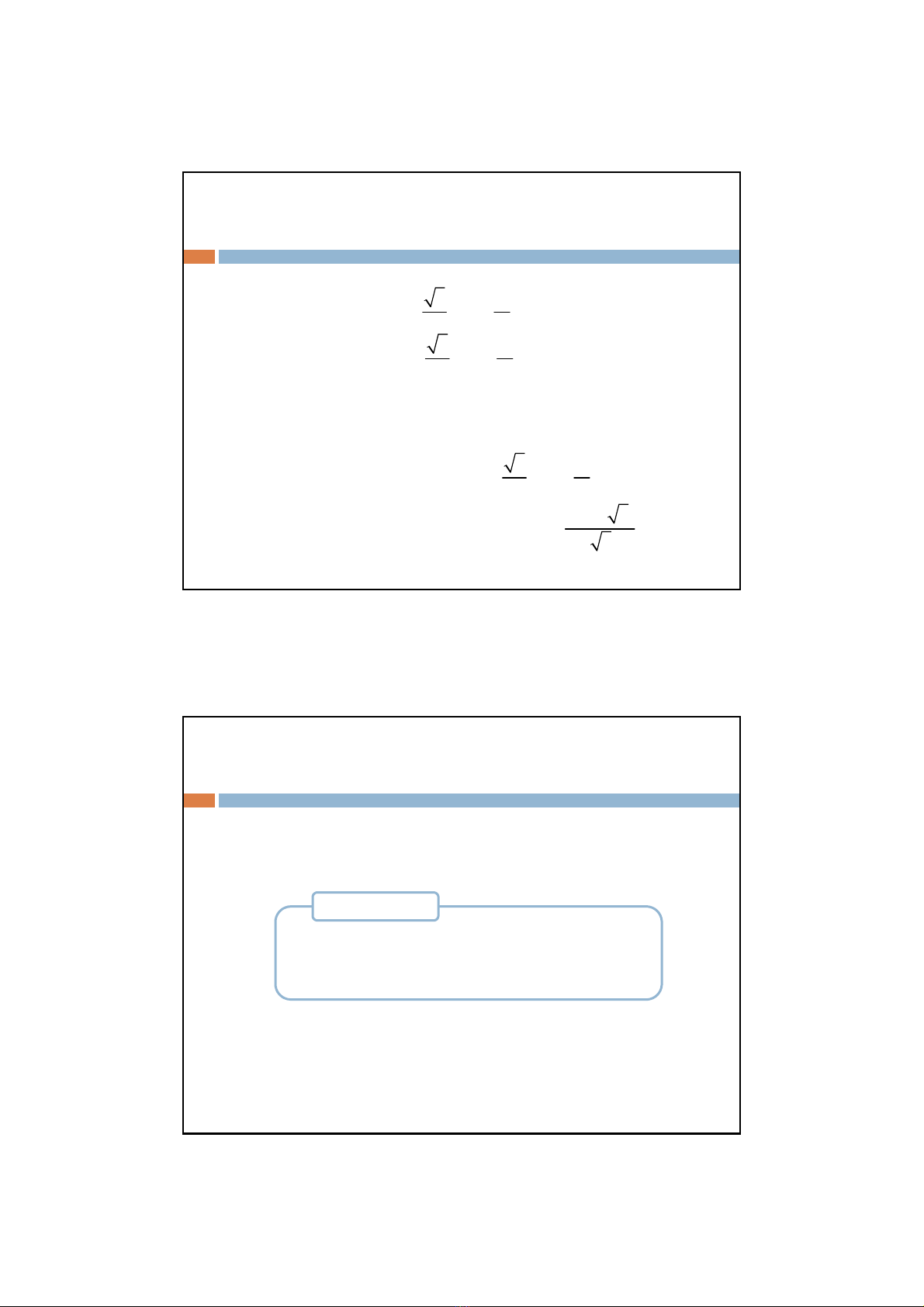
Ví dụ:Cho cơcấu có liên kếtvàchịulựcnhưhình vẽ.TựatạiD
vớihệsốma sát trượttĩnh là ktbiếtrằng AB=BD=2BC=2a, lựcF
có điểmđặttạiCvàcóphương thẳng đứng.
1) LựcFbằng bao nhiêu để thanh BD không trượttạiD.
2) PhảnlựctạiAvàD
y
x
A
C
FB
q
= 60o
D
CHƯƠNG 4 Ma sát
2. Bài toán cân bằng có kể đến ma sát
Phân tích lực
q
A
BAx
Ay
By
Bx
C
F
= 60o
D
B
By
Bx
ND
Fms
Xét thanh AB cân bằng
Xét thanh BD cân bằng
0
20
22.0
x
y
A
xx
yy
y
AB
AB
F
Fqa
Maqaa
B



(1)
(2)
(3)
0
0
.30
2
x
y
D
ms x
Dy
yx
FB
NB
B
F
FF
a
MaFa
B



(4)
(5)
(6)
(1,2,3,4,5) và (6) ta lậpđược6phương trình 6 ẩn
Bài giảng Cơ học Lý thuyết - Tuần 4 3/21/2011
Giảng viên Nguyễn Duy Khương 4
CHƯƠNG 4 Ma sát
2. Bài toán cân bằng có kể đến ma sát
yqBa
Từ(3)
Thếvào (6) ta được3
32
x
F
Bqa




Thếvào (4) ta được3
32
ms
F
qa
F



Điềukiệnđể thanh BD không trượtmaxmtDsNFF k
D
NFqa
Thếvào (5) ta được
3()
32
t
qa k qa
FF




13
2231
t
t
k
Fqa k

CHƯƠNG 5 Trọng tâm
1. Trọng tâm củavậtrắn
2. Trọng tâm của nhiềuvậtrắnđồng chất
NỘI DUNG
Bài giảng Cơ học Lý thuyết - Tuần 4 3/21/2011
Giảng viên Nguyễn Duy Khương 5
CHƯƠNG 5 Trọng tâm
1. Trọng tâm của vật rắn
kk
C
kk
C
kk
C
vx
xV
vy
yV
vz
zV
Ba chiều
kk
C
kk
C
s
x
xS
sy
yS
Hai chiều
Với xc, yc, zclà tọa độ trọng tâm hệ nhiều vật
xk, yk, zklà tọa độ trọng tâm của từng vật trong hệ
sklà diện tích của từng vật trong hệ, S=s1+s2+…
vklà thể tích của từng vật, V=v1+v2+…
CHƯƠNG 5 Trọng tâm
2. Trọng tâm của nhiều vật rắn đồng chất
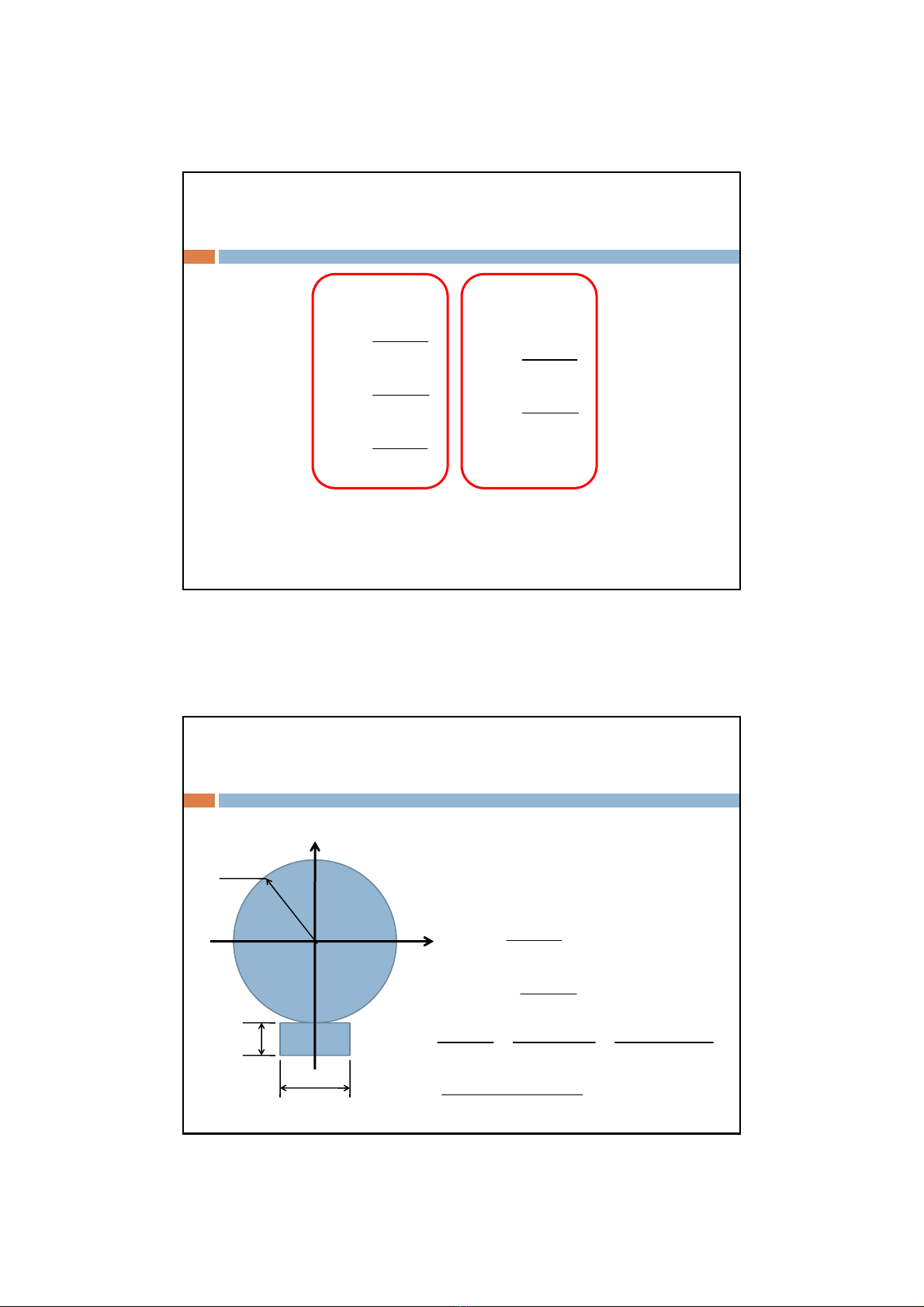
Ví dụ: Cho các hình sau đây, tìm trọng tâm của hình
Vì hình có tính đốixứng qua trụcy
nên trọng tâm của hai hình phải
nằmtrêntrụcy
0
kk
C
kk
C
sx
xS
sy
yS
2
11 2 2 1 2
2
12
kk
C
sy Sy Sy R y bhy
ySSS Rbh



2
00,3.0,2.(0,6) 0, 04( )
3,14.0, 5 0, 3.0, 2 m

0, 3bm
0, 2hm
0,5
R
m
x
y