Bài giảng Cơ Học Lý Thuyết - Tuần 9 5/5/2011
Giảng viên Nguyễn Duy Khương 1
Bài tập áp dụng
CHƯƠNG 11 Nguyên lý D’Alembert
MB
r
Q
A
P
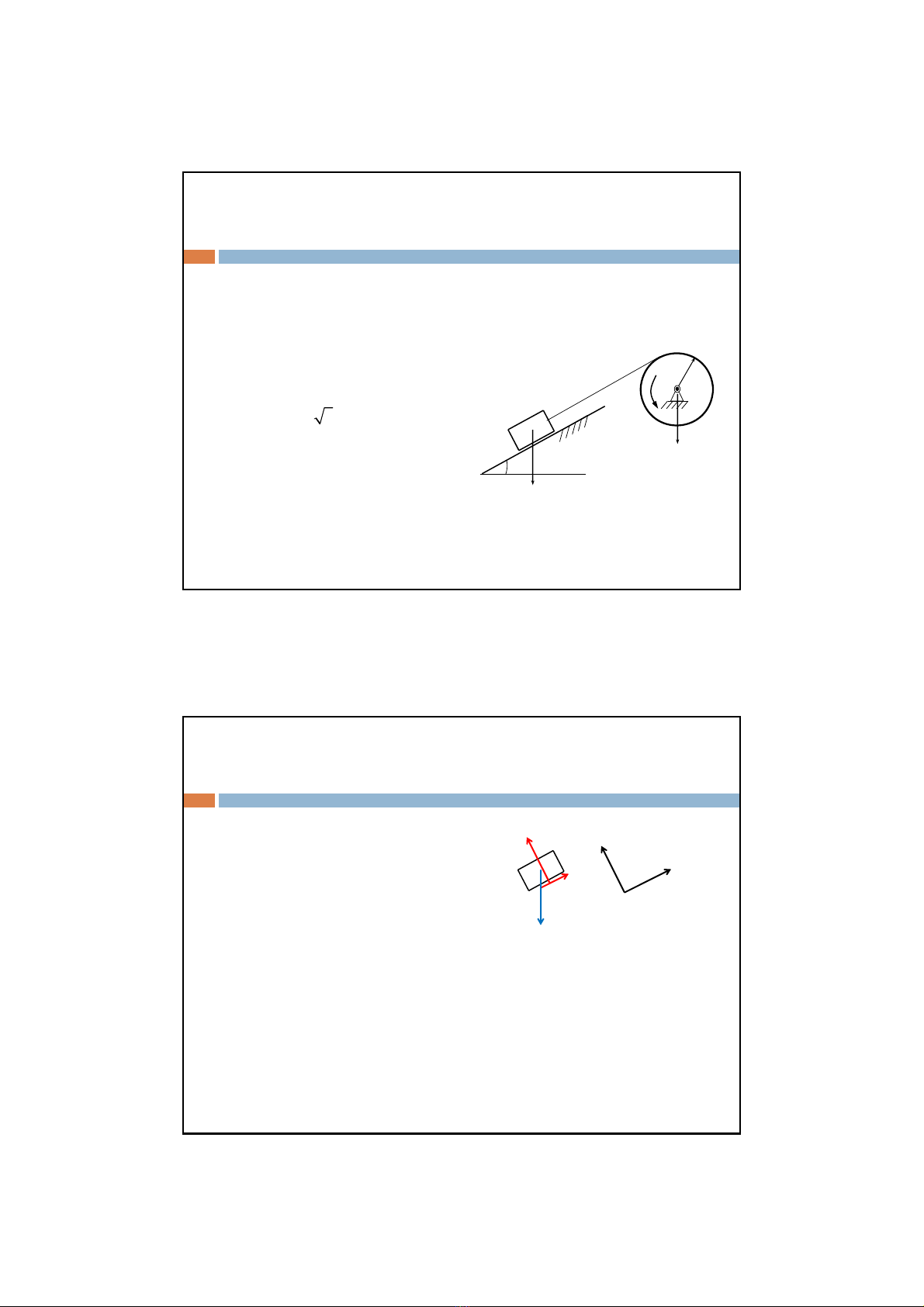
Ví dụ:Dây không khốilượng, mềm, không giãn và không trượttrên
ròng rọc. Ròng rọc B là vành tròn đồng chất, bán kính r. Trọng lượng
củavậtAvàròngrọc B là P và Q. Cho P, Q, M = const, r, ;hệsốma
sát tĩnh, động giữaAvàmặt nghiêng lầnlượtlàf
t,f
đ.Bỏqua ma sát ở
khớpbảnlềB. Hệban đầuđứng yên.
1) Tìm điềukiệncủa góc nghiêng để
vậtAtrượtđượctrênmặt nghiêng.
2) Cho ft=,>30
0, dây luôn
căng. Xác định gia tốccủavậtA
dướidạng hàm củar,P,Q,M.
3) Xác định lựccăng dây.
4) Tìm điềukiệncủaMđể dây nốivậtA
bịchùng. Xác định lạigiatốcvậtA
và gia tốcgóccủaròngrọcBtrong
trường hợp này.
3/3
Bài tập áp dụng
CHƯƠNG 11 Nguyên lý D’Alembert
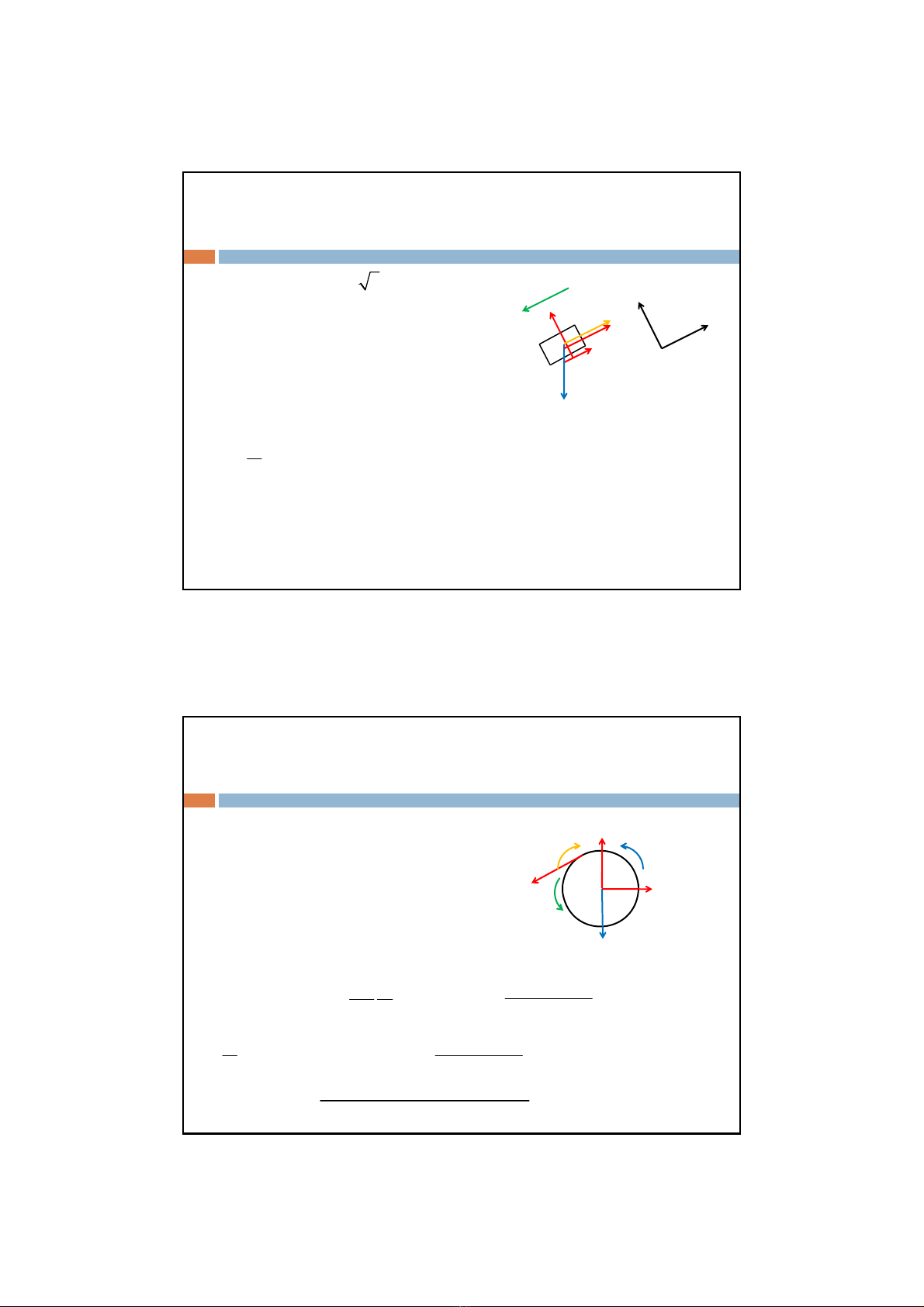
1)Tìm điềukiệncủa góc nghiêng để vậtAtrượtđượctrênmặt nghiêng.
Bỏ qua lực căng dây T=0
A
Phân tích lực tác động lên A
N
Fms
P
Xét vật A cân bằng đứng yên
sin 0
cos 0
x
y
ms
FP
FP
F
N


yx
sin
cos
ms
F
N
P
P
Để vật A trượttrênmặtphẳng nghiêng t
ms
F
f
N
sin cos
t
PfP
tan t
arctan t
f
Bài giảng Cơ Học Lý Thuyết - Tuần 9 5/5/2011
Giảng viên Nguyễn Duy Khương 2
Bài tập áp dụng
CHƯƠNG 11 Nguyên lý D’Alembert
2)Vớiđiềukiện
Thỏa điều kiện trên nên vật A trượt được
A
Phân tích lực tác động lên A N
Fms
P
Xét vật A chuyểnđộng tịnh tiếncânbằng
sin 0
cos 0
qt msx
y
FP
NP
FF T
F


yx
Hai phương trình 3 ẩn nên không giải được, ta xét thêm ròng rọc B
3/3
t
f0
,30
WA
Fqt
T
sin 0
cos 0
Ad
WN TP
N
Pf
g
P


(1)
(2)
Bài tập áp dụng
CHƯƠNG 11 Nguyên lý D’Alembert
Xét chuyển động ròng rọc B
Phân tích lực tác động lên ròng rọc B
B
T
Q
M
y
B
x
B
qt
B
M
cos 0
sin 0
0
xx
yy
qt
BB
FBT
FBQT
MrTMM



(3)
(4)
(5)
(5) 0
O
rM
TJ

20
AQ
TrW
Mr
rg
 AQr g
r
Tg
W
M
 (6)
Thế (2) và (6) vào (1) ta có:
cos sin 0
A
dA
Qr MgPfP P
g
W
gr
W


((sin cos) )
()
d
A
gPr
rP Q
W
f
M

Bài giảng Cơ Học Lý Thuyết - Tuần 9 5/5/2011
Giảng viên Nguyễn Duy Khương 3
Bài tập áp dụng
CHƯƠNG 11 Nguyên lý D’Alembert
A
WQ
M
T
g
r

3)Lựccăng dây T
((sin cos) )
()
d
gPr f M QM
rP Q
g
r


((sin cos) )
()
d
PQr
f
M
rP Q

ĐiềukiệncủaM để dây bịchùng 0T
((sin cos) )
0
()
d
PQr f
rP
M
Q
(sin cos )
d
Qr f
M

Bài tập áp dụng
CHƯƠNG 11 Nguyên lý D’Alembert
Khi dây bị chùng để tính gia tốc của A và ròng rọc B ta thế T=0 vào
phương trình (1), (2) và (5) ta được
sin 0
cos 0
0
d
qt
O
A
PgfgP
P
M
W
N
M
N



2
cos
(sin cos )
Ad
P
gf
Mg
Qr
N
W

Bài giảng Cơ Học Lý Thuyết - Tuần 9 5/5/2011
Giảng viên Nguyễn Duy Khương 4
Bài tập áp dụng
CHƯƠNG 11 Nguyên lý D’Alembert
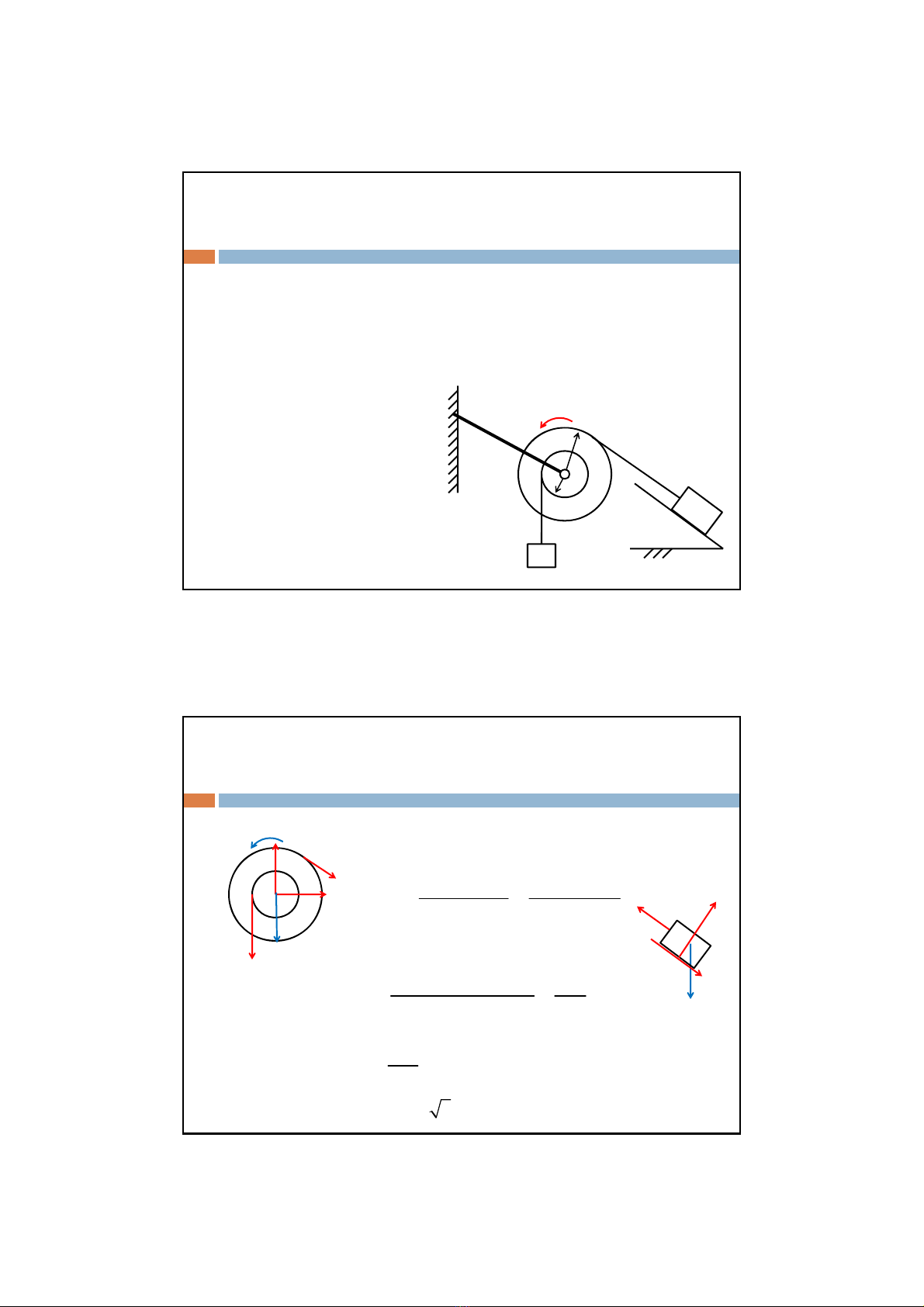
Ví dụ:Cho tảiAkhốilượng m1,tảiBkhốilượng m2, ròng rọcCcókhối
lượng m3với các bán kính R1=2R
2=2R
0, bán kính quán tính đốivớitrục
qua C là , thanh CD=4R0,khốilượng m4.Chohệsốma sát trượttĩnh và
động tạiBvớimặtphẳng nghiêng là ftvà fd.Bỏqua khốilượng dây và
ma sát ổtrục, giảsửhệban đầuđứng yên.
1. Tìm điềukiệnngẫuMđể Btrượtđược.
2. Xác định gia tốctảiAvàB.
3. Tính phảnlực liên kếttạiD.
(Biếtm
1=m2=m3/3=m4/4=m0
=R
1/3=2R0/3)
A
M
1
R
2
R
30o
B
C
D
60o
Bài tập áp dụng
CHƯƠNG 11 Nguyên lý D’Alembert
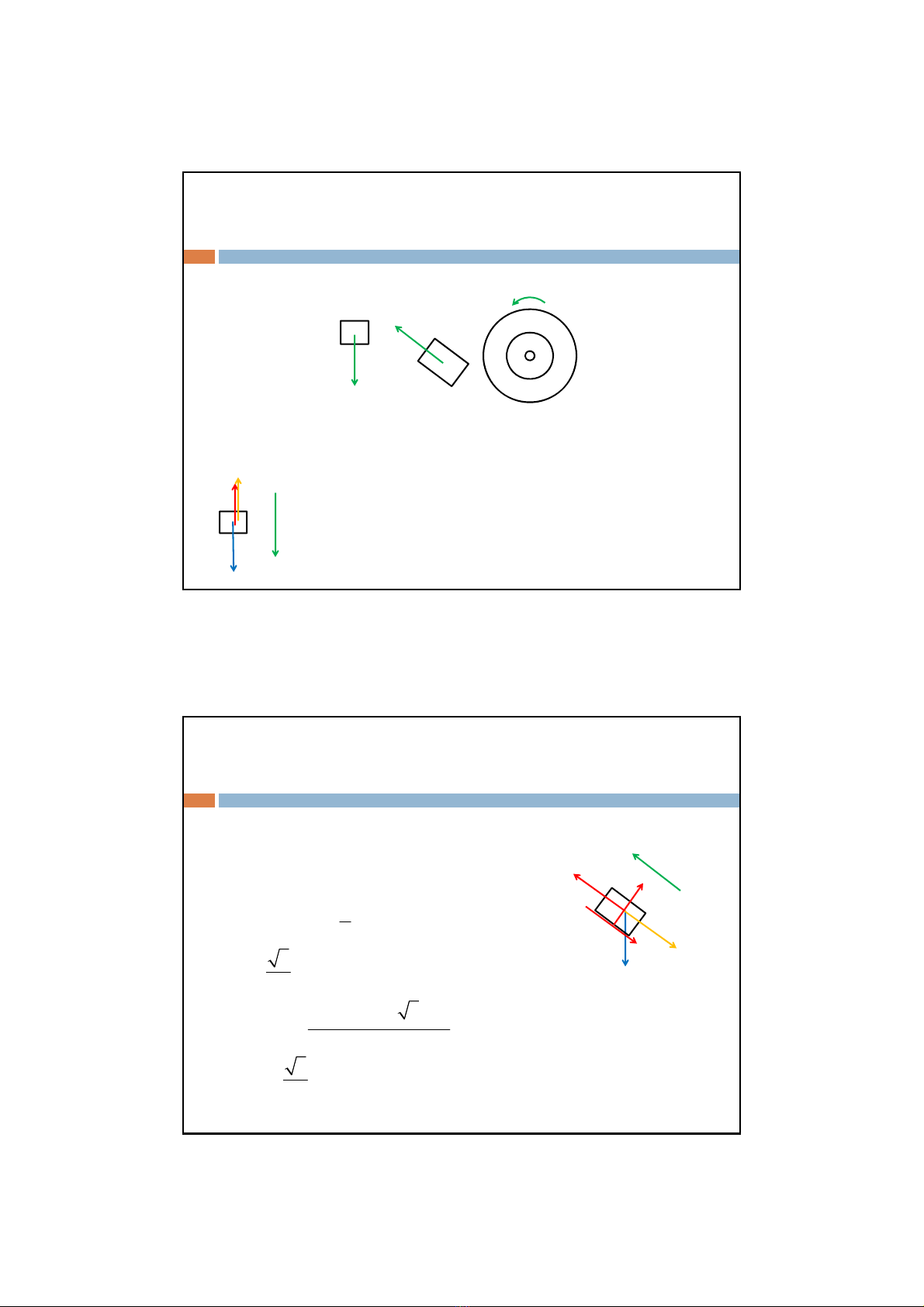
1)Tìm điềukiệncủangẫuMđể vậtBtrượtđượctrênmặt nghiêng.
M
C
x
C
y
C
A
T
B
T
PB
B
B
T
N
ms
F
21
0
CBA
MMRT TR

01 00
00
22
B
M
Rmg M Rmg
RR
T

2sin 30 0
Bms
o
x
Fmg
TF
012
00
22
ms
MRgmm
M
RR
F

Để vật B trượtđượctrênmặtphẳng nghiêng tms
F
f
N
2
0
cos 30
2
o
t
fm g
R
M

00
3t
Rm
M
g
f
Xét ròng rọcC cânbằng:
Xét tảiB cânbằng:
Q
Bài giảng Cơ Học Lý Thuyết - Tuần 9 5/5/2011
Giảng viên Nguyễn Duy Khương 5
Bài tập áp dụng
CHƯƠNG 11 Nguyên lý D’Alembert
2)Xác định gia tốctảiAvàB
*Quan hệđộng học
20A
WR R

10
2
B
WR R

A
A
W
C
B
B
W
Xét chuyểnđộng củatảiA:
0
qt
AA
yA
TFPF
11
0
AA
mmgTW
A
P
A
Tqt
A
F
A
W
(1)
10
A
AA
TW
mWgmg
Bài tập áp dụng
CHƯƠNG 11 Nguyên lý D’Alembert
Xét chuyểnđộng củatảiB:
sin 30 0
cos 30 0
qt
Bms B
o
xB
o
yB
FP
FP
FF T
N


22
2
10
2
3
2
BBd
WN Tmf mg
mg
N

B
W
PB
B
B
T
N
ms
F
qt
B
F

0
0
431
2
3
2
A
B
d
W
T
N
gf
m
mg

(2)
(3)