Bài giảng Cơ Học Lý Thuyết - Tuần 12 5/23/2011
Giảng viên Nguyễn Duy Khương 1
2. Nguyên lý di chuyển khả dĩ
CHƯƠNG 13 Nguyên lý di chuyểnkhảdĩ
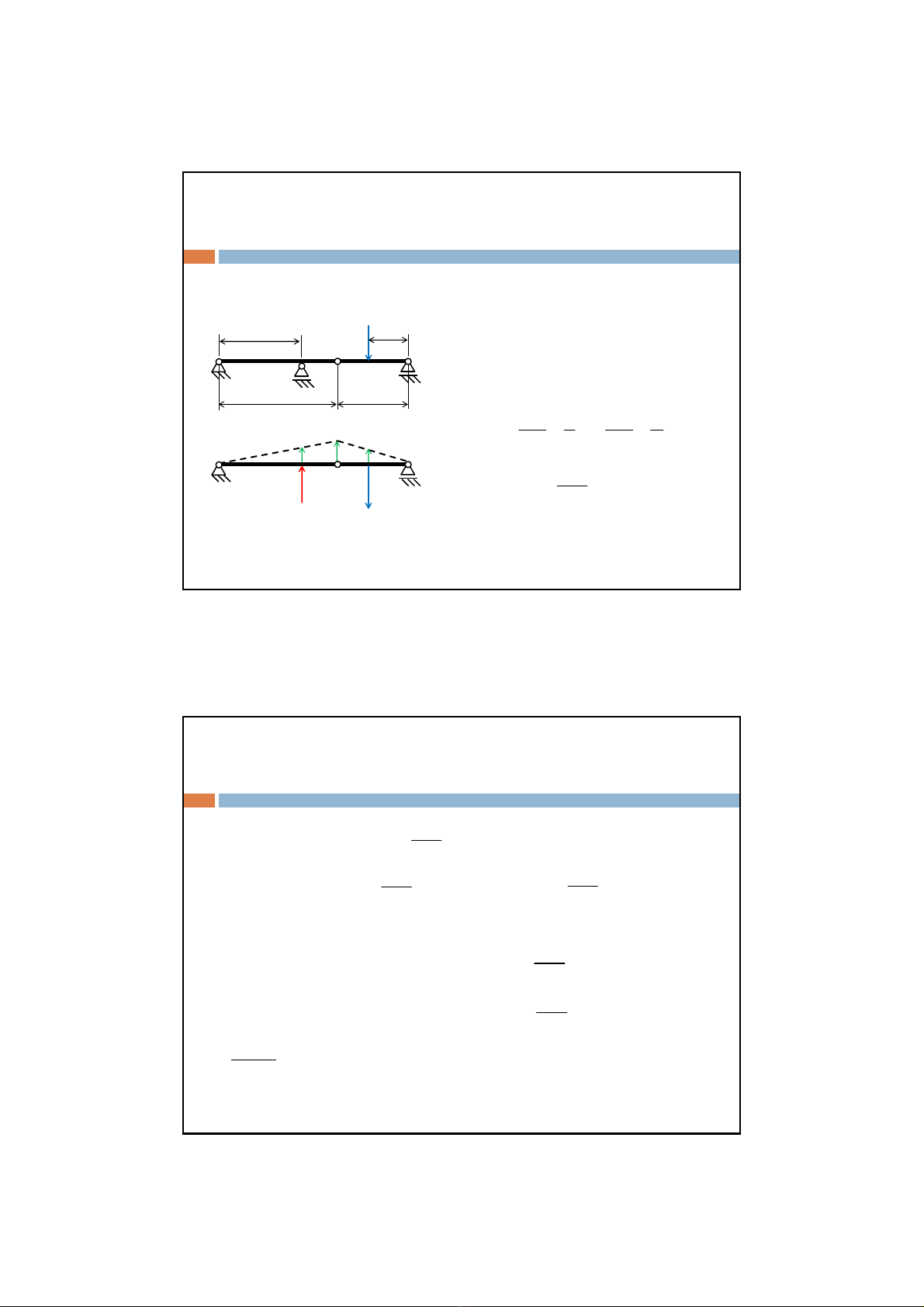
Ví dụ:Cho hệcó cơcấunhưhình vẽ.Bỏqua trọng lượng củadầm,
hãy xác định áp lựclêngốiB
Giải
Để tính phảnlực liên kếttạiBtagiải
phóng liên kết và thay vào đóphảnlực
NB. Sau đóchohệdi chuyểnkhảdĩ,
và ta có điềukiện sau:
1
B
C
sa
s
l
Do đó:
1
2
E
B
bl
s
s
al
Tính công khảdĩta được
() ()
B
A
AN AP

A
BC
D
E
P
ab
1
l2
l
B
s
C
s
E
s
2
E
C
sb
s
l
A
BC
D
E
P
B
N
B
BE
Ns Ps
2. Nguyên lý di chuyển khả dĩ
CHƯƠNG 13 Nguyên lý di chuyểnkhảdĩ
1
2
B
BB
bl
A
Ns P s
al


1
2
B
B
bl
NPs
al




Điềukiệnđể hệcân bằng 0Q
1
2
B
bl
QN P
al

1
2
0
B
bl
NP
al

1
2
B
bl
NP
al

Chú ý: Nếutadùngbằng phương pháp tĩnh họcbìnhthường thì sẽ
dài vì phảilậpphương trình cân bằngcho2dầm AC và CD. Vì thế
ta dùng cách này sẽngắnhơnrất nhiều.
Bài giảng Cơ Học Lý Thuyết - Tuần 12 5/23/2011
Giảng viên Nguyễn Duy Khương 2
2. Nguyên lý di chuyển khả dĩ
CHƯƠNG 13 Nguyên lý di chuyểnkhảdĩ
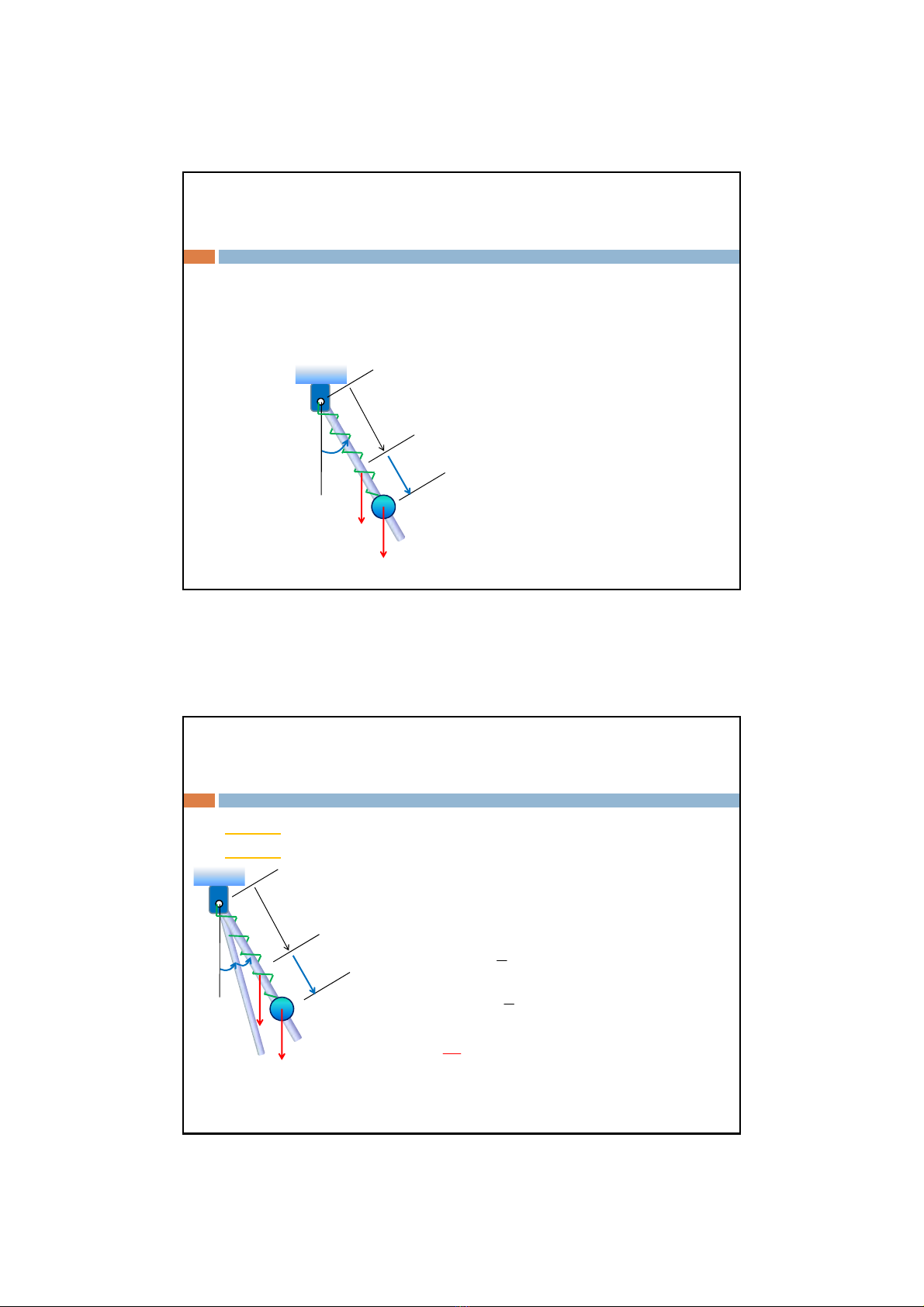
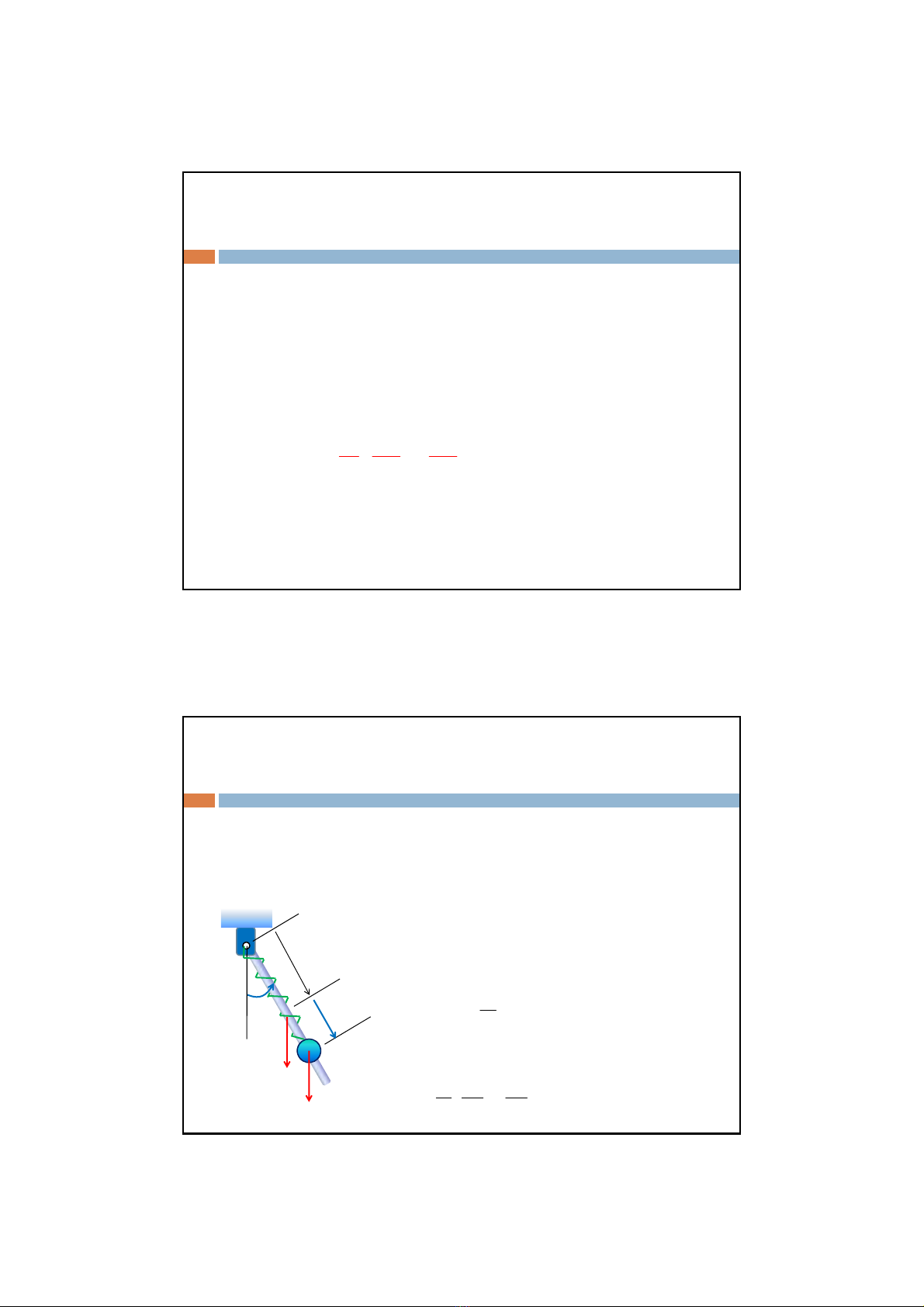
Ví dụKhông kểđến ma sát, hãy xác định các lựcsuyrộng củahệbao
gồm thanh AB đồng chấtchiềudàil,trọng lượngPvàcóthểqua quanh
trụcAtrênmặtphẳng thẳng đứng. Viên bi M trọng lượng Q chuyểnđộng
trên thanh. Chiều dài tựnhiên củalòxoAMlàl0,độ cứng bằng k.
Q
B
A
P
0
l
x
1
2
q
qx
Chọntọađộ suy rộng
2. Nguyên lý di chuyển khả dĩ
CHƯƠNG 13 Nguyên lý di chuyểnkhảdĩ
Cách 1: Tính lựcsuyrộng bằng định nghĩa(tựtính)
Cách 2: Tính lựcsuyrộng bằng công khảdĩ
Cho 12
0, 0qqx


Tính Q1:
Q
B
A
P
0
l
x
1() ()
A
AP AQ

Tính công khảdĩ
0
sin sin ( )
2
l
PQlx
 

0
sin sin ( )
2
l
PQlx


10
sin ( )sin
2
Pl
QQlx

Bài giảng Cơ Học Lý Thuyết - Tuần 12 5/23/2011
Giảng viên Nguyễn Duy Khương 3
2. Nguyên lý di chuyển khả dĩ
CHƯƠNG 13 Nguyên lý di chuyểnkhảdĩ
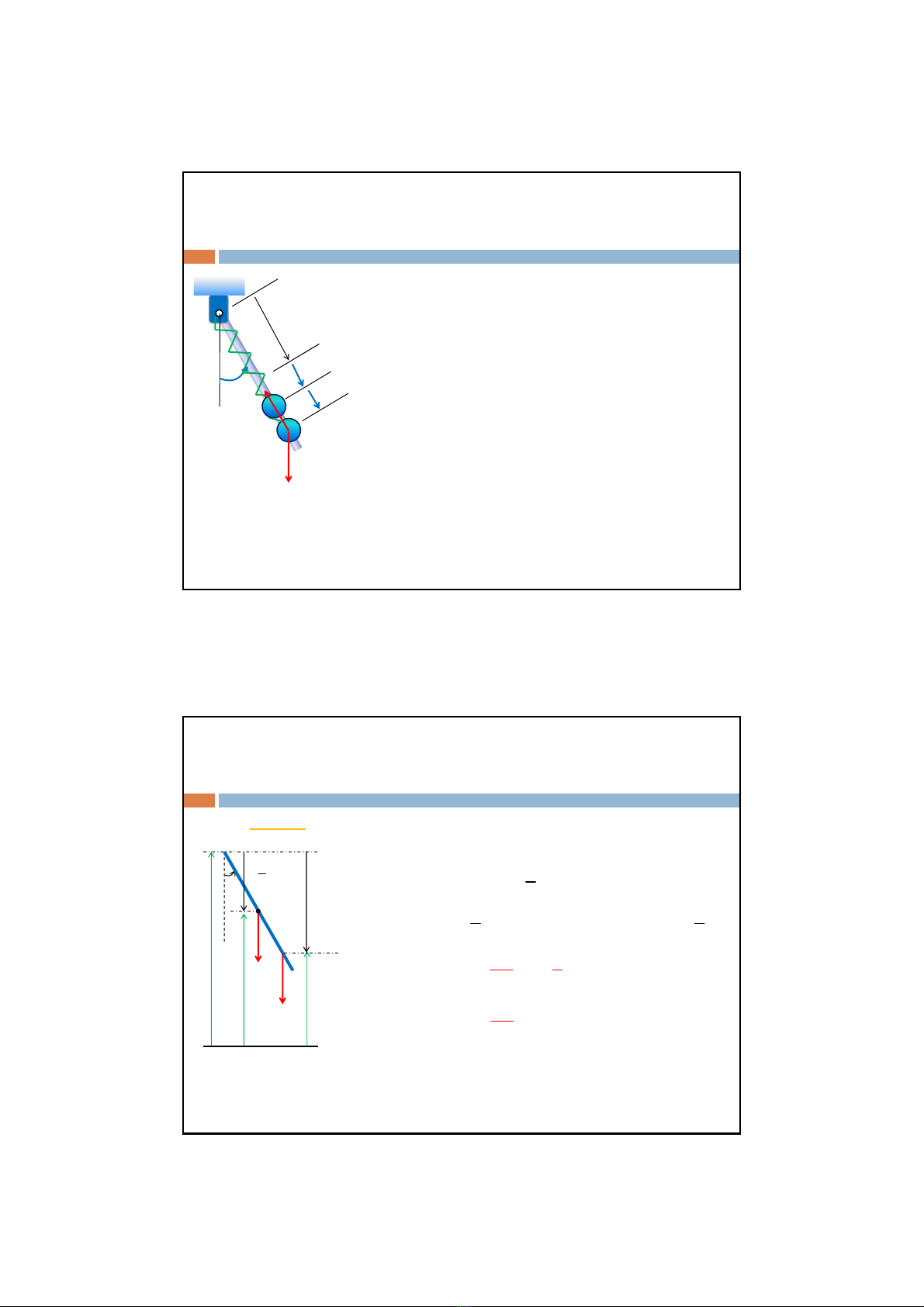
Cho 12
0, 0qqx


Tính Q2:
1() ( )
s
A
AQ AF

Tính công khảdĩ
cos s
QxFx


cosQkxx

2cosQQ kx

Q
B
A
s
F
0
l
x
x
cosQxkxx


2. Nguyên lý di chuyển khả dĩ
CHƯƠNG 13 Nguyên lý di chuyểnkhảdĩ
Cách 3: Tính lựcsuyrộng bằng hàm thếnăng
() () ( )
s
VP VQ VF

2
1
2
PQ
P
yQy kx

2
0
1
(cos)(()cos)
22
AA
l
P
yQylxkx


10
sin ( )sin
2
l
QQ P Qlx


2cos
x
QQ Q kx
x


A
cos
2
l
P
B
I
Q
P
y
Q
y
A
y
0
()coslx

Chọnmứcthếnăng
bằng 0 (bấtkỳ)
Bài giảng Cơ Học Lý Thuyết - Tuần 12 5/23/2011
Giảng viên Nguyễn Duy Khương 4
CHƯƠNG 14 Phương trình tổng quát động lựchọcvàphương
trình Lagrange II
2. Phương trình Lagrange II
NỘI DUNG
1. Phương trình tổng quát động lưchọc
1. Phương trình tổng quát động lực học
CHƯƠNG 14 Phương trình tổng quát động lựchọcvàphương
trình Lagrange II
Phương trình tổng quát động lực học



1
0
N
kx k k k ky k k k kz k k k
k
Fmxx Fmy y Fmz z




  
Từphương trình tổng quát động lựchọc, ta biểudiễntheohệtọa
độ suy rộng đầyđủ và độclậptuyến tính
Phương trình Lagrange II

1
0
N
kkkk
k
FmW r


11
rr
iii
ii
ii
dT TqQq
dt q q












i
ii
dT T
Q
dt q q



Bài giảng Cơ Học Lý Thuyết - Tuần 12 5/23/2011
Giảng viên Nguyễn Duy Khương 5
2. Phương trình Lagrange II
CHƯƠNG 14 Phương trình tổng quát động lựchọcvàphương
trình Lagrange II
Trường hợpcáclựccóthế
0
ii
dL L
dt q q





Nếutấtcảcác lựctácdụng lên hệlà các lựccóthế, thì áp dụng
công thứcsau
LT
Hàm L củacáctọađộ suy rộng và vậntốcsuyrộng bằng hiệugiữa
động năng và thếnăng củahệ,đượcgọi là hàm Lagrange hay hàm
thế.Khiđóphương trình Lagrange củacáclựccóthếcó dạng:
Đây là hệphương trình vi phân chuyểnđộng củacơhệ.Sốlượng
phương trình bằng đúng sốbậctựdo củahệ.
2. Phương trình Lagrange II
CHƯƠNG 14 Phương trình tổng quát động lựchọcvàphương
trình Lagrange II
Ví dụKhông kểđếnmasát,viếtphương trình chuyểnđộng củahệbao
gồm thanh AB đồng chấtchiềudàil,trọng lượngPvàcóthểqua quanh
trụcAtrênmặtphẳng thẳng đứng. Viên bi M trọng lượng Q chuyểnđộng
trên thanh. Chiều dài tựnhiên củalòxoAMlàl0,độ cứng bằng k.
Q
B
A
P
0
l
x
1
2
q
qx
Chọntọađộ suy rộng
10
sin ( ) sin
2
Pl
QQlx

2cosQQ kx

Lựcsuyrộng
Phương trình Lagrange II
i
ii
dT T
Q
dt q q




