Bài giảng Cơ Lý Học Thuyết - Tuần 13 5/25/2011
Giảng viên Nguyễn Duy Khương 1
2. Phương trình Lagrange II
CHƯƠNG 14 Phương trình tổng quát động lựchọcvàphương
trình Lagrange II
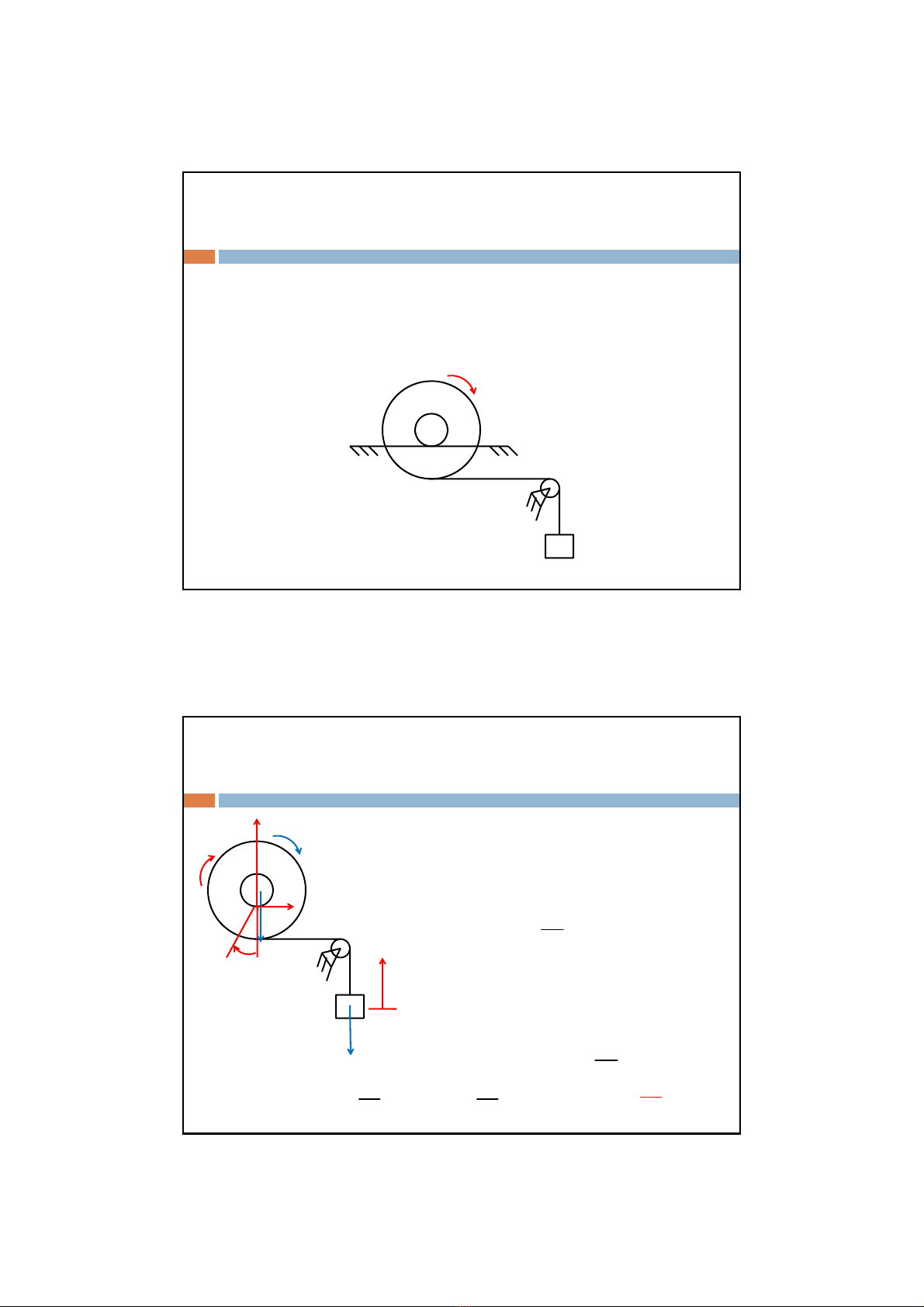
Ví dụ:Cho tảiAkhốilượng m1,conlănkhốilượng m2, các bán kính
R=3r và bán kính quán tính đốivớitrục qua tâm là .Biếtconlănlăn
không trượt, bỏqua khốilượng dây và ma sát lăn, giảsửhệban đầu
đứng yên. Xác định vậntốc, gia tốctảiA.
A
B
I
H
M
2. Phương trình Lagrange II
CHƯƠNG 14 Phương trình tổng quát động lựchọcvàphương
trình Lagrange II
Cơhệmộtbậctựdo nên ta chọnhệtọađộ suy
rộng q1=h
*Tính lựcsuyrộng Q1
Cho hệmột DCKD từvịtrí ban đầu: tảiAđilên
2
h
r

Công di khảdĩ
() () ()
kA B
A
AP AP AM


A
B
I
H
M
h
A
P
P
I
N
ms
F
0
A
Ph M


2
A
h
PhM r

1
22
kA A
MM
A
Ph Pq
rr





12
A
M
QP
r
Bài giảng Cơ Lý Học Thuyết - Tuần 13 5/25/2011
Giảng viên Nguyễn Duy Khương 2
2. Phương trình Lagrange II
CHƯƠNG 14 Phương trình tổng quát động lựchọcvàphương
trình Lagrange II
*Tính động năng
AB
TT T
222
12
111
222
AB B
mV J m V

22
22
12 2
2
11 1
22424
AA
A
VV
mV m m
r

222
2
12
2
4( )1
24 A
rm r m V
r




222
2
12
2
4( )1
24
rm r m h
r




*Tính các đạohàm
222
12
2
1
4( )
4
rm r m
TT h
qr
h






222
12
2
1
4( )
4
rm r mdT h
dt q r









1
;0
T
q
2. Phương trình Lagrange II
CHƯƠNG 14 Phương trình tổng quát động lựchọcvàphương
trình Lagrange II
*Áp dụng phương trình Lagrange II
i
ii
dT T
Q
dt q q





222
12
2
4( ) 0
42
A
rm r m M
hP
rr






1
11
dT T
Q
dt q q






1
222
12
2
24( )
A
Mrmg
hW r
rm r m
 

Bài giảng Cơ Lý Học Thuyết - Tuần 13 5/25/2011
Giảng viên Nguyễn Duy Khương 3
2. Phương trình Lagrange II
CHƯƠNG 14 Phương trình tổng quát động lựchọcvàphương
trình Lagrange II
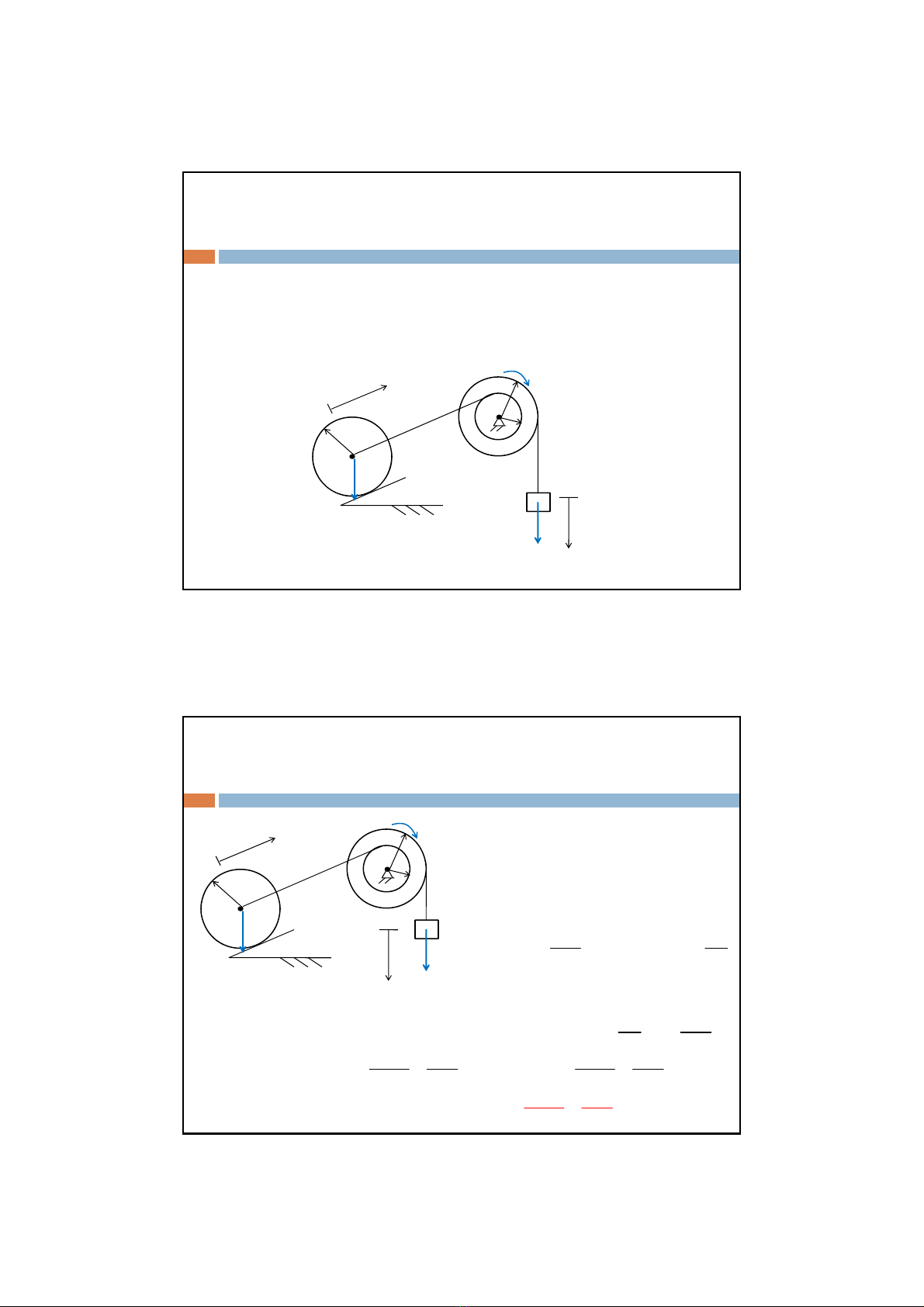
Ví dụ:Cho tảiAtrọng lượng PA,conlăntrụtròn B khốilượng PB,ròng
rọcCkhốilượng PCcác bán kính R1=2R2=2R0và bán kính quán tính
đốivớitrục qua tâm là .Biếtconlănlăn không trượt, bỏqua khối
lượngdâyvàmasátlăn, giảsửhệban đầuđứng yên. Xác định vận
tốc, gia tốctảiA.
B
s
B
A
M
B
P
A
P
C
1
R
1
R
2
R
h
2. Phương trình Lagrange II
CHƯƠNG 14 Phương trình tổng quát động lựchọcvàphương
trình Lagrange II
Cơhệmộtbậctựdo nên ta chọnhệ
tọađộ suy rộng q1=h
*Tính lựcsuyrộng Q1
Cho hệmột DCKD từvịtrí ban đầu:
tảiAđixuống
0
2
h
R

Công di khảdĩ
() () ()
kA B
A
AP AP AM


sin
AB B
PhP s M


0
sin 22
AB
hh
PhP MR


1
00
sin sin
22 22
kAB AB
MM
A
PP h PP q
RR






1
0
sin
22
AB
M
QPP R

B
s
B
A
M
B
P
A
P
C
1
R
1
R
2
R
h
0
;2
B
h
sR


Bài giảng Cơ Lý Học Thuyết - Tuần 13 5/25/2011
Giảng viên Nguyễn Duy Khương 4
2. Phương trình Lagrange II
CHƯƠNG 14 Phương trình tổng quát động lựchọcvàphương
trình Lagrange II
*Tính động năng
ABC
TT T T 2222
1111
2222
AB
ABBBCC
PP
VVJJ
gg




*Tính các đạohàm
222
00
2
10
32 9 8
32
ABC
RP RP P
TT h
qRg
h






222
00
2
10
32 9 8
32
ABC
RP RP P
dT h
dt q R g

 






1
;0
T
q
22 2
22
22
0
1111 1
22422424
C
ABABA A
A
P
PPVPV V
V
g
gggR




222
2
00
2
0
32 9 8
1()
232
ABC
A
RP RP P V
Rg

222
2
00
2
0
32 9 8
1()
232
ABC
RP RP P h
Rg

2. Phương trình Lagrange II
CHƯƠNG 14 Phương trình tổng quát động lựchọcvàphương
trình Lagrange II
*Áp dụng phương trình Lagrange II
i
ii
dT T
Q
dt q q





222
00
2
00
32 9 8 sin
0
32 2 2
ABC
AB
RP RP P
M
hPP
Rg R






1
11
dT T
Q
dt q q






00
0222
00
2sin
16 32 9 8
AB
ABC
RP RP M
hgR
RP RP P
 

Bài giảng Cơ Lý Học Thuyết - Tuần 13 5/25/2011
Giảng viên Nguyễn Duy Khương 5
2. Phương trình Lagrange II
CHƯƠNG 14 Phương trình tổng quát động lựchọcvàphương
trình Lagrange II
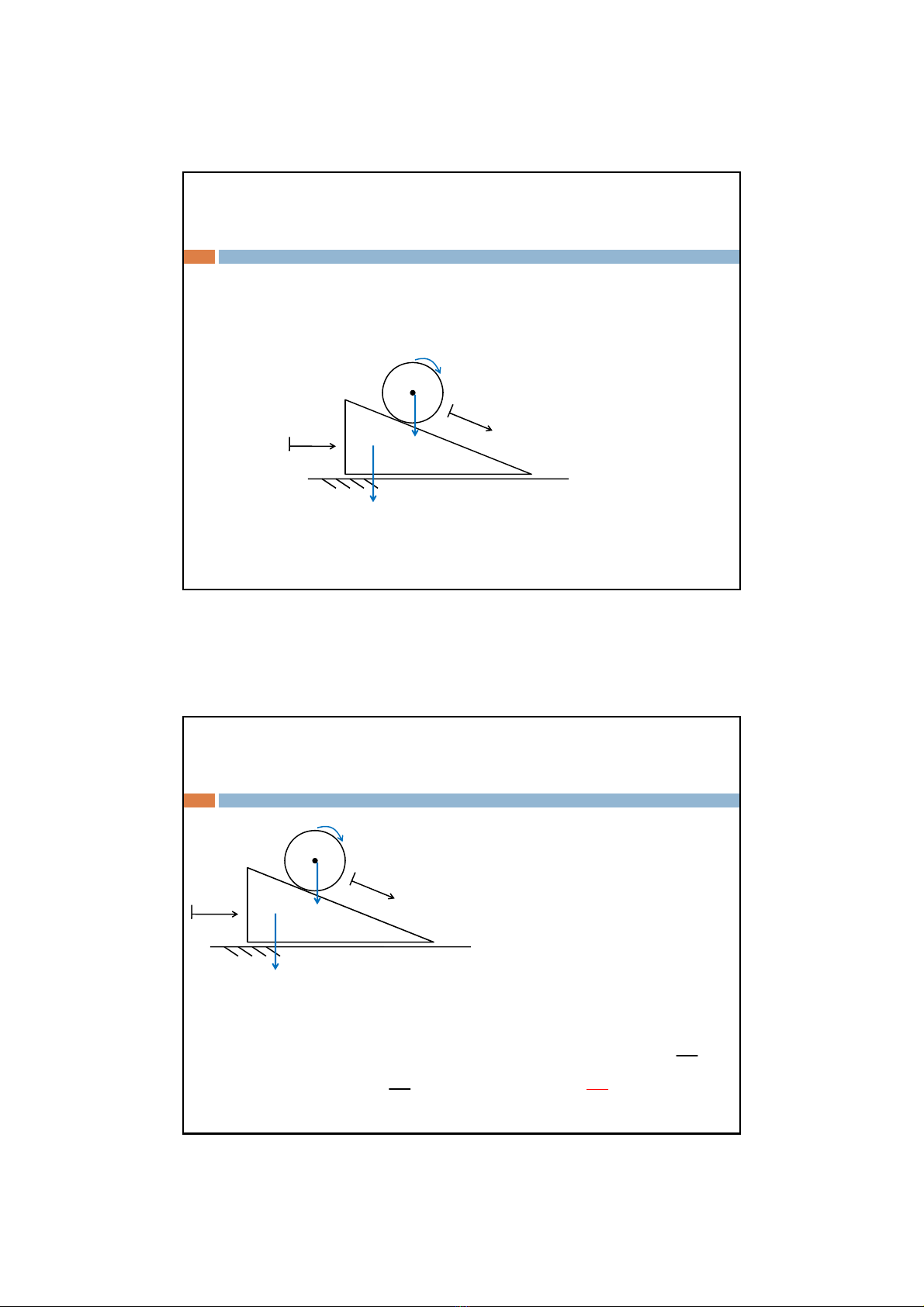
Ví dụ:Cho lăng trụAnhưhình vẽkhốilượng m1con lăntrụtròn đồng
chấttâmBkhốilượng m2,conlănlăn không trượt, bỏqua ma sát trượt
giữaAvànền, giảsửhệban đầuđứng yên. Xác định gia tốcAvàB.
A
B
M
x
s
B
P
A
P
2. Phương trình Lagrange II
CHƯƠNG 14 Phương trình tổng quát động lựchọcvàphương
trình Lagrange II
Cơhệhai bậctựdo nên ta chọnhệtọađộ suy
rộng q1=x độ dờilăng trụA, q2=s độ dờitương
đốicủatâmBvớilăng trụA
*Tính lựcsuyrộng Q1
Cho hệmột DCKD đặcbiệt
10qx
() () ()
kA B
A
AP AP AM


000 0
 10Q
A
B
M
x
s
B
P
A
P
2
;0qs
(GắnchặtBvàolăng trụA)
*Tính lựcsuyrộng Q2
Cho hệmột DCKD đặcbiệt10qx
2
;0qs
() () ()
kA B
A
AP AP AM


0sin
B
s
Ps M
R


(sin )
B
M
P
s
R
 22
sin
M
Qmg R