
Trường ĐH Bách khoa tp Hồ Chí Minh
Khoa Khoa học ứng dụng - Bộ môn Toán ứng dụng
------------------------------------------------------
Đại số tuyến tính
KHÔNG GIAN VECTƠ
Giảng viên TS Đặng Văn Vinh

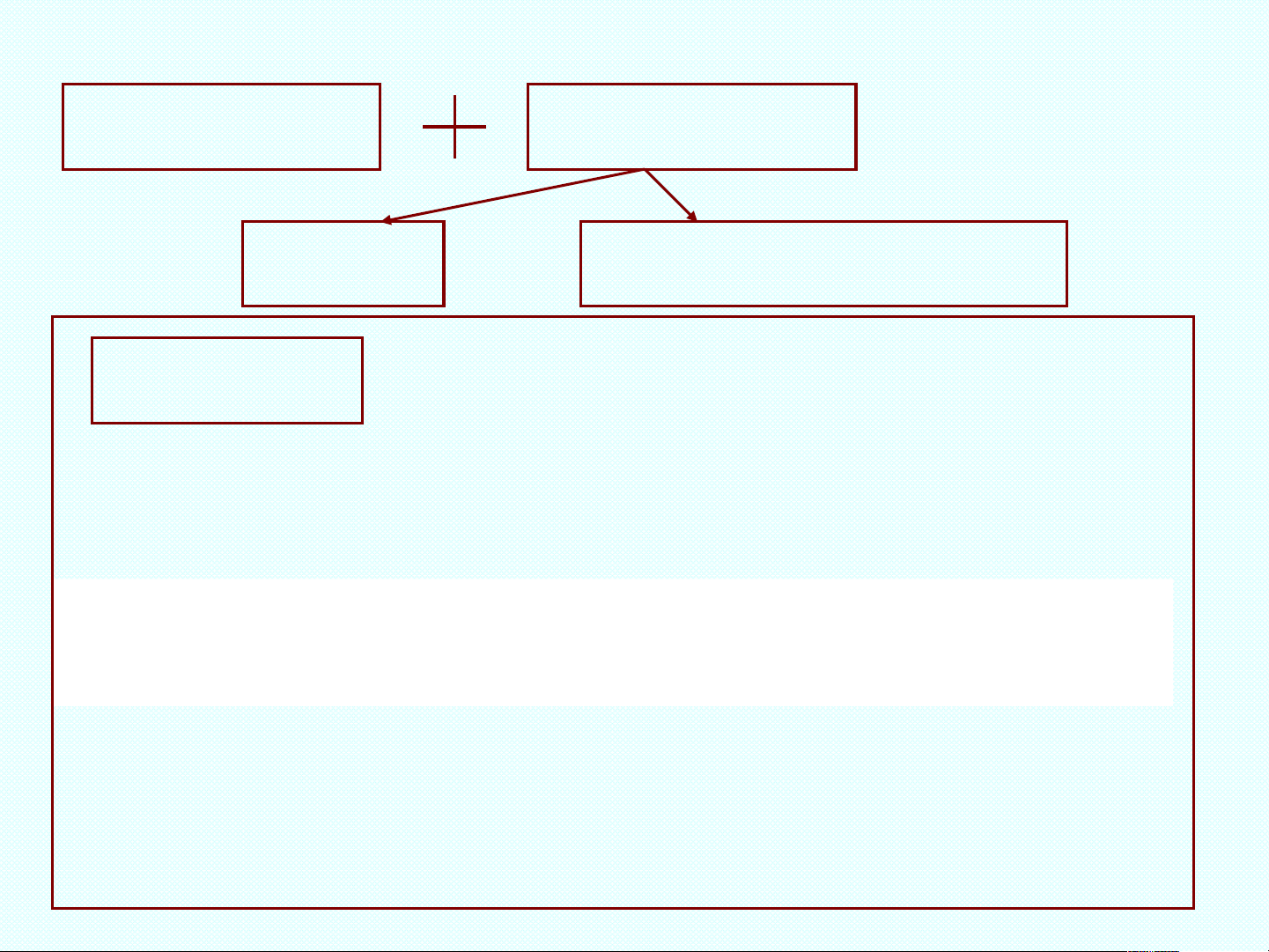
Nội dung
---------------------------------------------------------------------------------------------------
------------------------
I – Định nghĩa và ví dụ
V – Không gian con.
II – Độc lập tuyến tính, phụ thuộc tuyến tính
IV – Cơ sở và số chiều
III – Hạng của hệ vectơ
KHÔNG GIAN VÉCTƠ V
I. Định nghĩa và các ví dụ
---------------------------------------------------------------------------------------------------
------------------------
2. (x + y) + z = x + (y + z)
3. Tồn tại véc tơ không, ký hiệu 0 sao cho x + 0 = x
4. Mọi x thuộc V, tồn tại vectơ, ký hiệu –x sao cho x + (-x) = 0
1. x + y = y + x;
8. 1x = x
Tập khác rỗng V Hai phép toán
Nhân véctơ với 1 sốCộng
8 tiên đề
5. Với mọi số và mọi vector x:
, K
( )x x x
6. Với mọi số , với mọi :
K
x,y V( x y ) x y
7. ( )x ( x)

I. Định nghĩa và các ví dụ
---------------------------------------------------------------------------------------------------
------------------------
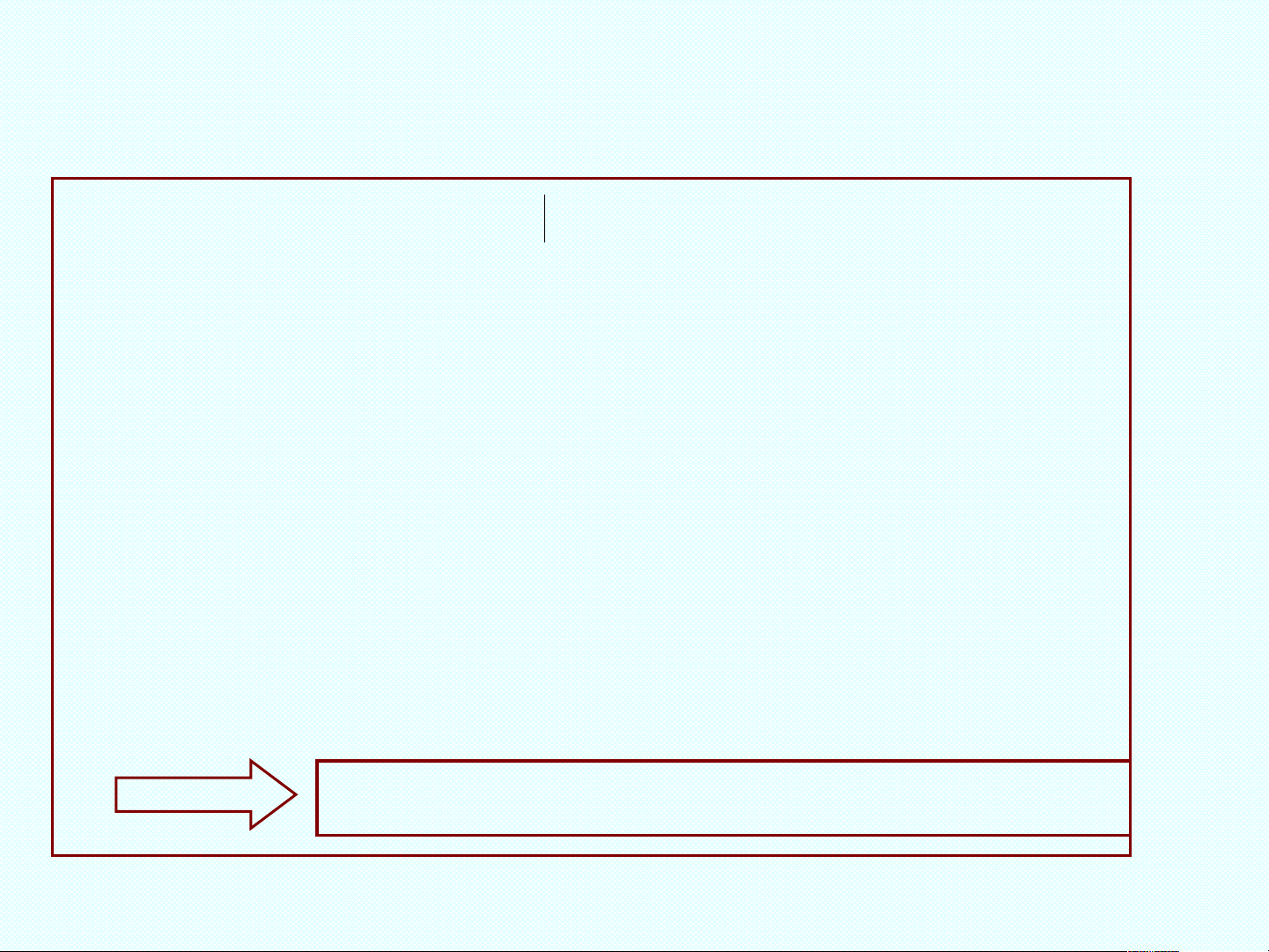
3) 0x = 0
5) -x = (-1)x
Tính chất của không gian véctơ
1) Véctơ không là duy nhất.
2) Phần tử đối xứng của véctơ x là duy nhất.
Với mọi vectơ x thuộc V và mọi số :
K
4) 0 0
I. Định nghĩa và các ví dụ
--------------------------------------------------------------------------------------
----------------------
RxxxxV i ),,( 3211
),,(),,(),,( 332211321321 yxyxyxyyyxxxyx
),,(),,( 321321 xxxxxxx
33
22
11
yx
yx
yx
yx
Ví dụ 1
V1 - Không gian véctơ trên trường số thực
3
R
Định nghĩa phép cộng hai véctơ như sau:
Định nghĩa phép nhân véctơ với một số thực như sau:
Định nghĩa sự bằng nhau:










![Bài giảng Đại số tuyến tính ThS. Nguyễn Hữu Hiệp [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250815/nganga_07/135x160/889_bai-giang-dai-so-tuyen-tinh-ths-nguyen-huu-hiep.jpg)















