powerpoint.vn
ĐỘNG LỰC HỌC CÔNG TRÌNH
ĐỘNG LỰC HỌC CÔNG TRÌNH
PGS. TS Dương Văn Thứ
2powerpoint.vn
CHƯƠNG 1: DAO ĐỘNG CỦA HỆ CÓ MỘT BẬC TỰ DO
1.1 MỘT SỐ KHÁI NIỆM CƠ BẢN VỀ LÝ THUYẾT DAO ĐỘNG
1.1.1 Khái niệm về chu kỳ và tần số
M
0
yP(t)
Hình 1.1
K
Tuỳ thu c vào quan h gi a l c lò xo và bi n d ng c a lò xo là tuy n ộ ệ ữ ự ế ạ ủ ế
tính , hay phi tuy n, mà ta có ếbài toán dao đ ng tuy n tính hay dao ộ ế
đ ng phiộ tuy n.ế
Dao đ ng c a v t thu n túy do l c lò xo sinh ộ ủ ậ ầ ự
ra khi M d ch chuy n kh i v trí cân b ng ban ị ể ỏ ị ằ
đ u (do m t nguyên nhân b t kỳ nào đó gây ầ ộ ấ
ra r i m t đi) đ c g i là ồ ấ ượ ọ dao đ ngộ t doự hay
là dao đ ng riêngộ.
D ng chuy n v c a v t M đ c g i là ạ ể ị ủ ậ ượ ọ d ng dao đ ng ạ ộ
riêng. N u trong quá trình dao đ ng luôn luôn t n t i l c ế ộ ồ ạ ự
đ ng P(t), ta có bài toán ộdao đ ng c ng b cộ ưỡ ứ . L c đ ng ự ộ
P(t) còn đ c g i là ượ ọ l c kích thích.ự
3powerpoint.vn
CHƯƠNG 1: DAO ĐỘNG CỦA HỆ CÓ MỘT BẬC TỰ DO
Số các dao động toàn phần của khối lượng thực hiện trong một đơn
vị thời gian, chỉ phụ thuộc vào các đặc trưng cơ học của hệ, gọi là
tần số dao động riêng hay tần số dao động tự do, và được ký hiệu là
f.
Thời gian để thực hiện một dao động toàn phần được gọi là chu kỳ
dao động, và được ký hiệu là T.
Nếu T đo bằng giây (s) (trong Động lực học công trình thời gian
thường được đo bằng giây), thì thứ nguyên của f là 1/s. Về trị số f và
T là nghịch đảo của nhau.
4powerpoint.vn
CHƯƠNG 1: DAO ĐỘNG CỦA HỆ CÓ MỘT BẬC TỰ DO
1.1.2 Dao động điều hoà và véc tơ quay
Sau đây ta xét m t d ng dao đ ng quan tr ng đ c g i là ộ ạ ộ ọ ượ ọ dao
đ ng đi u hòaộ ề . Đây là d ng dao đ ng c b n th ng g p trong ạ ộ ơ ả ườ ặ
c h c, m t khác, các dao đ ng có chu kỳ luôn luôn có th ơ ọ ặ ộ ể
phân tích thành các d ng dao đ ng đi u hòa đ n gi n. ạ ộ ề ơ ả
Xét dao đ ng đi u hòa, ộ ề
( ) sinS t A t
ω
=
(1-1)
( ) os tv t A c
ω ω
=
(1-2)
Có v n t cậ ố
2
( ) sina t A t
ω ω
= −
(1-3)và gia t cố
5powerpoint.vn
CHƯƠNG 1: DAO ĐỘNG CỦA HỆ CÓ MỘT BẬC TỰ DO
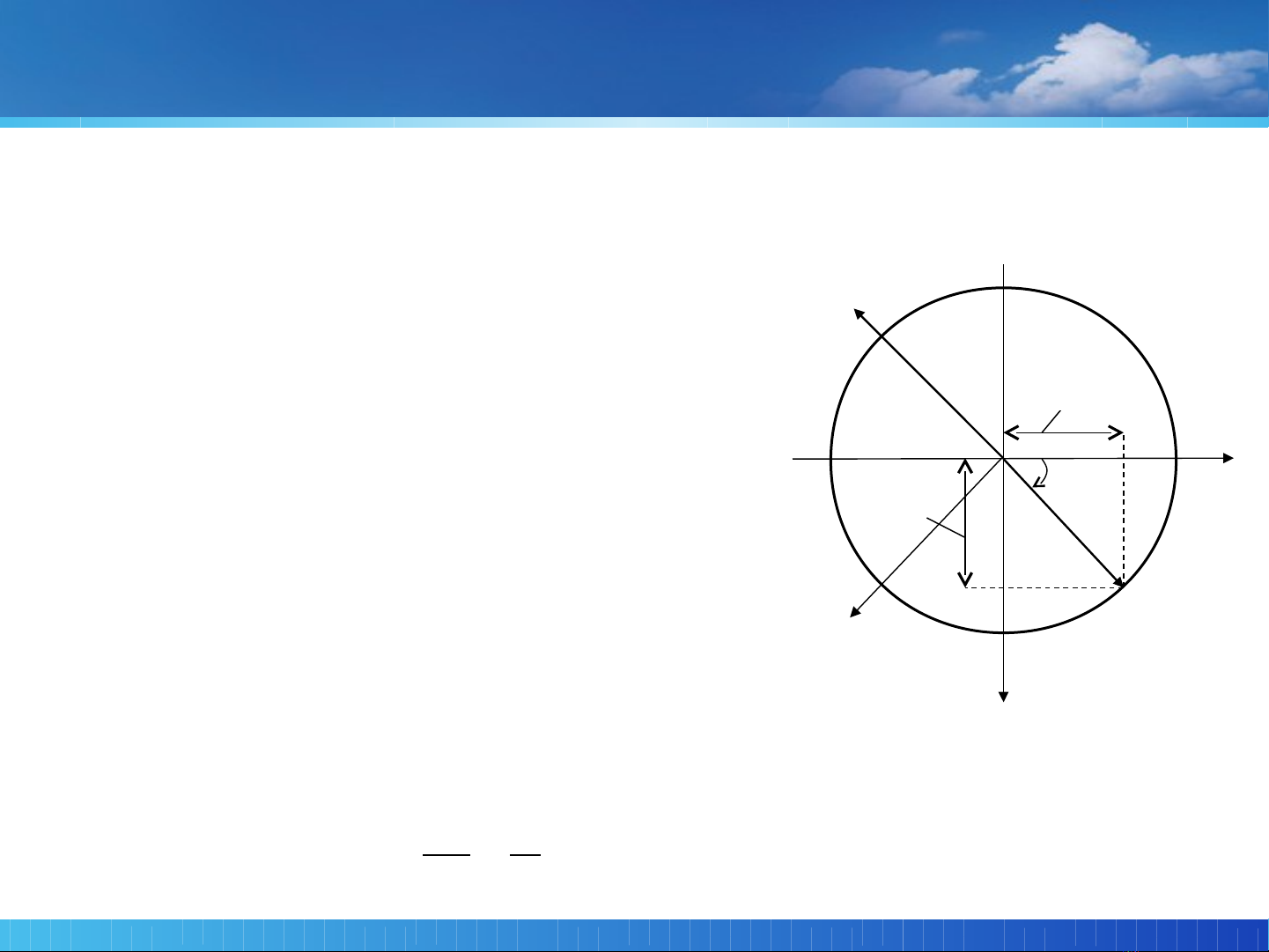
1.1.2 Dao động điều hoà và véc tơ quay
Tr s A đ c g i là ị ố ượ ọ biên độ dao đ ng, ộ
còn v n t c góc ậ ố ω đ c g i là ượ ọ t n sầ ố
vòng c a dao đ ng – là s dao đ ng ủ ộ ố ộ
toàn ph n c a h th c hi n trong 2ầ ủ ệ ự ệ π
giây.
Acosωt
Asinω
t
x
s
0
Hình 1.2
A
ωt
a
r
v
r
Theo đ nh nghĩa, ị
2T
ω π
=
2 1
Tf
π
ω
= =
2f
ω π
=
nên do đó
Có th miêu t chuy n đ ng này nh ể ả ể ộ ư
chuy n d ch c a đi m mút véc t OA (có ể ị ủ ể ơ
đ l n b ng A) lên m t tr c S nào đó khi ộ ớ ằ ộ ụ
véc t này quay quanh đi m c đ nh O ơ ể ố ị
v i v n t c góc ớ ậ ố ω.(xem hình 1.2).