Định lý cơ bản của vi tích phân
Ứng dụng hình học của tích phân
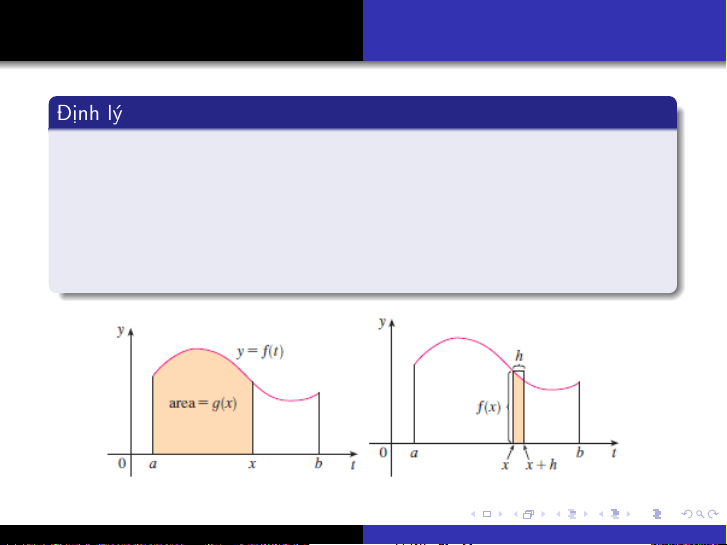
1Định lý cơ bản của vi tích phân
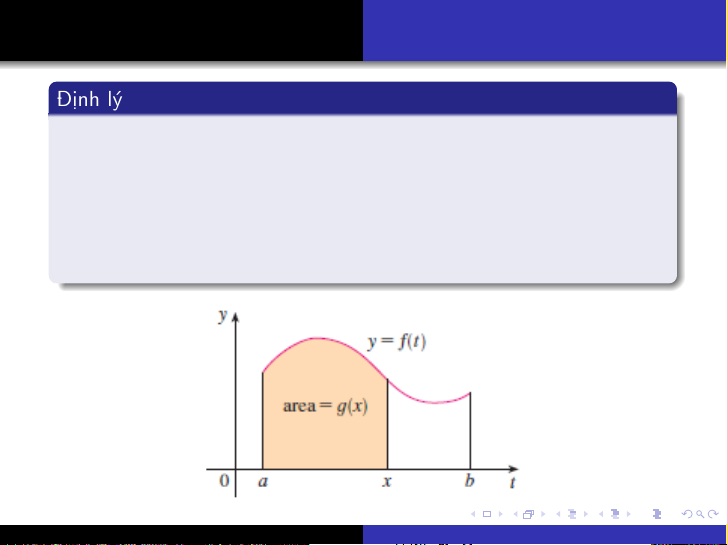
Định lý cơ bản
Công thức Newton - Leibnitz
2Ứng dụng hình học của tích phân
Diện tích hình phẳng
Thể tích vật thể
Chiều dài đường cong
Diện tích mặt tròn xoay
TS. Đào Huy Cường (Bộ môn Toán Ứng Dụng) Giải tích 1 (Calculus 1)
Định lý cơ bản của vi tích phân
Ứng dụng hình học của tích phân Định lý cơ bản
Công thức Newton - Leibnitz
Định lý
Nếu fliên tục trên [a,b], thì hàm số gđịnh bởi
g(x) = Zx
a
f(t)dt
liên tục trên [a,b], và g0(x) = f(x)với mọi x∈(a,b)
TS. Đào Huy Cường (Bộ môn Toán Ứng Dụng) Giải tích 1 (Calculus 1)
Định lý cơ bản của vi tích phân
Ứng dụng hình học của tích phân Định lý cơ bản
Công thức Newton - Leibnitz
Ví dụ
Tính đạo hàm của các hàm số:
(a) g(x) = Zx
0p1+t2dt;
(b) g(x) = Zx4
1cos tdt.
TS. Đào Huy Cường (Bộ môn Toán Ứng Dụng) Giải tích 1 (Calculus 1)
Định lý cơ bản của vi tích phân
Ứng dụng hình học của tích phân Định lý cơ bản
Công thức Newton - Leibnitz
Định lý
Nếu fliên tục trên [a,b], thì
Zb
a
f(x)dx =F(x)
b
a,
trong đó Flà một nguyên hàm bất kỳ của f.
TS. Đào Huy Cường (Bộ môn Toán Ứng Dụng) Giải tích 1 (Calculus 1)
Định lý cơ bản của vi tích phân
Ứng dụng hình học của tích phân
Diện tích hình phẳng
Thể tích vật thể
Chiều dài đường cong
Diện tích mặt tròn xoay
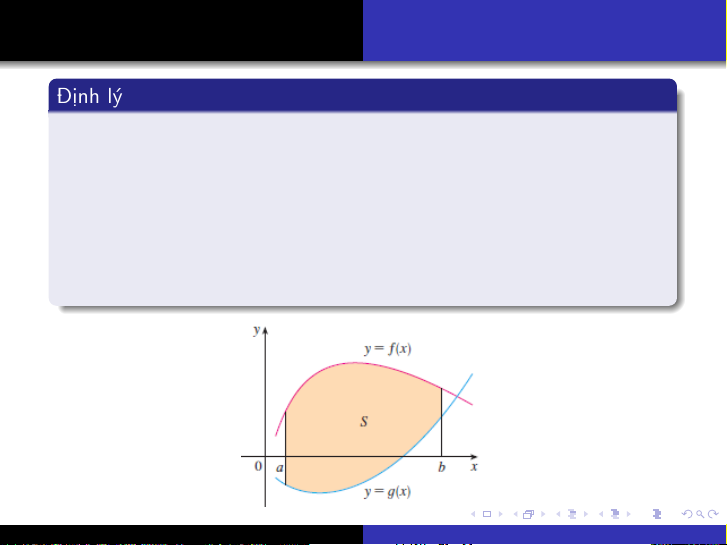
Định lý
Cho fvà glà hai hàm số liên tục và f(x)≥g(x)với mọi
x∈[a,b]. Miền phẳng nằm giữa hai đường cong y=f(x)và
y=g(x)và giữa hai đường thẳng đứng x=avà x=bcó diện
tích là
S=Zb
a
[f(x)−g(x)]dx.
TS. Đào Huy Cường (Bộ môn Toán Ứng Dụng) Giải tích 1 (Calculus 1)