Giới thiệu tài liệu
Trong phân tích định lượng, mô hình hồi quy là công cụ không thể thiếu để khám phá mối quan hệ giữa các biến. Tuy nhiên, độ tin cậy và hiệu lực của các mô hình này có thể bị ảnh hưởng nghiêm trọng bởi sự hiện diện của các khuyết tật. Một trong những khuyết tật phổ biến và quan trọng là hiện tượng đa cộng tuyến, nơi các biến độc lập có mối quan hệ tuyến tính chặt chẽ. Việc không phát hiện và xử lý đa cộng tuyến có thể dẫn đến ước lượng không hiệu quả, kiểm định giả thuyết sai lệch và kết luận không chính xác. Do đó, tài liệu này nhằm mục đích trang bị kiến thức về bản chất, tầm quan trọng của việc kiểm định và các phương pháp cụ thể để nhận diện khuyết tật này, từ đó nâng cao chất lượng và độ tin cậy của các mô hình hồi quy trong nghiên cứu và ứng dụng thực tiễn.
Đối tượng sử dụng
Sinh viên, nhà nghiên cứu và chuyên gia trong lĩnh vực kinh tế lượng, thống kê, tài chính và các ngành khoa học xã hội khác sử dụng mô hình hồi quy, đặc biệt là những người quan tâm đến việc kiểm định và xử lý các khuyết tật của mô hình để đảm bảo độ tin cậy của kết quả phân tích.
Nội dung tóm tắt
Tài liệu này tập trung vào việc kiểm định các khuyết tật của mô hình hồi quy, đặc biệt là hiện tượng đa cộng tuyến, một vấn đề thường gặp trong phân tích kinh tế lượng. Đa cộng tuyến xảy ra khi có mối quan hệ tuyến tính mạnh mẽ giữa các biến độc lập, làm cho việc ước lượng các hệ số hồi quy trở nên kém chính xác và không đáng tin cậy. Để giải quyết thách thức này, tài liệu giới thiệu hai phương pháp kiểm định chính thông qua hồi quy phụ. Phương pháp thứ nhất sử dụng chỉ số R-squared (R²*) của mô hình hồi quy phụ để đánh giá mức độ giải thích của biến độc lập mục tiêu, kết hợp với kiểm định F để xác định sự tồn tại của đa cộng tuyến. Cặp giả thuyết được đặt ra là H0: không có đa cộng tuyến (R²* = 0) và H1: có đa cộng tuyến (R²* > 0). Phương pháp thứ hai dựa trên việc kiểm định T cho từng hệ số hồi quy riêng lẻ (βi*) trong mô hình phụ, với giả thuyết H0: các hệ số bằng 0 (không có đa cộng tuyến) và H1: ít nhất một hệ số khác 0 (có đa cộng tuyến). Cả hai phương pháp đều cung cấp công thức tính toán thống kê kiểm định và cách xác định miền bác bỏ để đưa ra kết luận cuối cùng. Phần thực hành được minh họa bằng một ví dụ cụ thể, trình bày kết quả hồi quy và hướng dẫn cách sử dụng các chỉ số như T-ratio, R-Bar-Squared và F-statistic để đánh giá và đưa ra kết luận về sự tồn tại của đa cộng tuyến trong một mô hình hồi quy cho trước. Mục tiêu cuối cùng là trang bị cho người học khả năng phân tích và nhận diện khuyết tật mô hình, từ đó đưa ra các điều chỉnh phù hợp để đảm bảo tính hợp lệ và ý nghĩa của kết quả nghiên cứu.


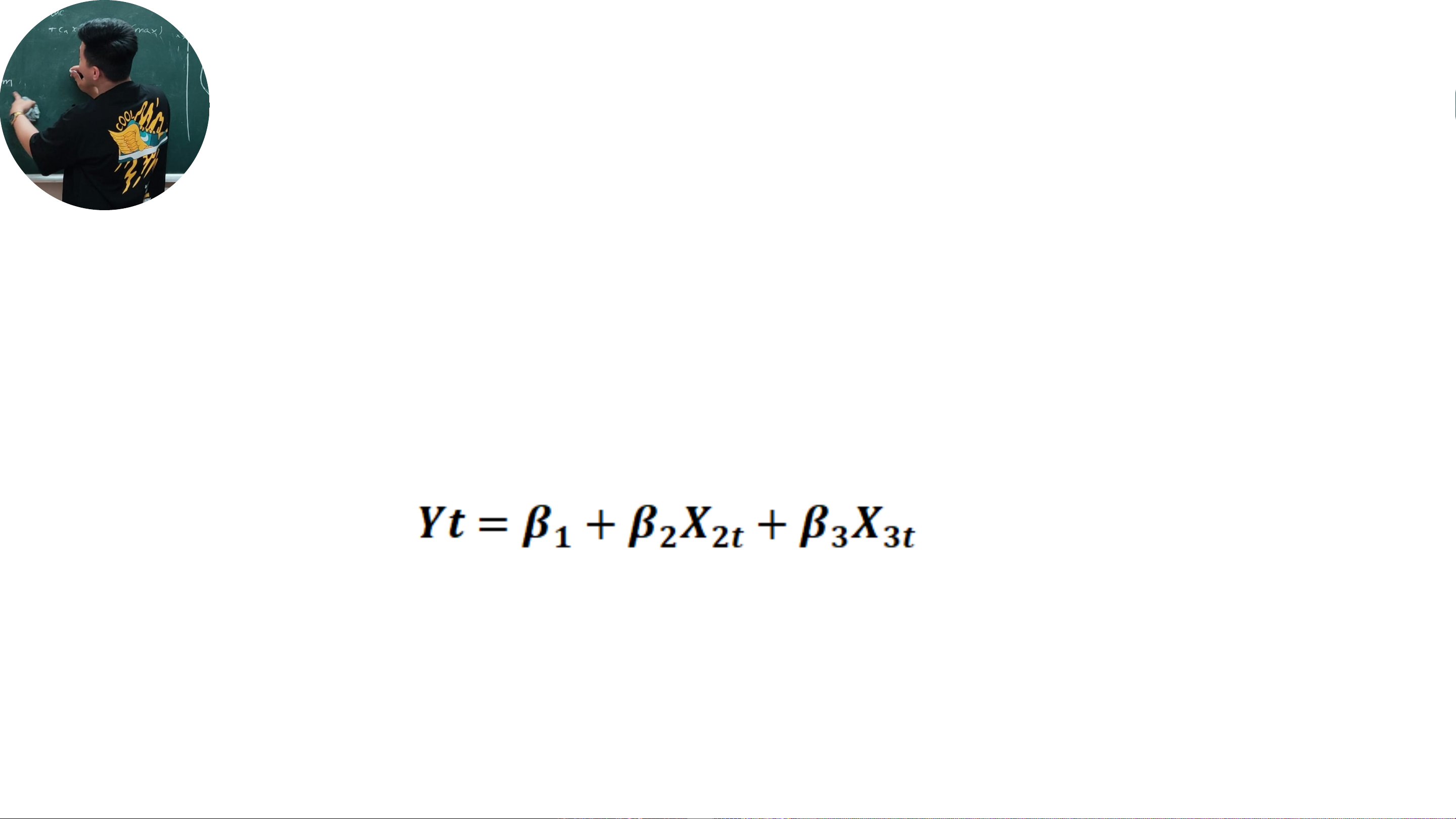







![Bài giảng Toán kinh tế: Chương 4 [Tóm tắt kiến thức trọng tâm]](https://cdn.tailieu.vn/images/document/thumbnail/2024/20240420/khanhchi2520/135x160/2769209_5773.jpg)
![Bài giảng Toán kinh tế: Chương 3 [mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2024/20240420/khanhchi2520/135x160/2769208_9497.jpg)
![Bài giảng Toán kinh tế Chương 2: [Thêm từ khóa hoặc mô tả liên quan]](https://cdn.tailieu.vn/images/document/thumbnail/2024/20240420/khanhchi2520/135x160/2769207_9194.jpg)

![Bài giảng Toán kinh tế: Chương 0 - Tổng quan [Chuẩn SEO]](https://cdn.tailieu.vn/images/document/thumbnail/2024/20240420/khanhchi2520/135x160/2769205_046.jpg)
















