Giới thiệu tài liệu
Tài liệu này giới thiệu về khái niệm tích phân suy rộng, một chủ đề quan trọng trong giải tích toán học.
Đối tượng sử dụng
Sinh viên các ngành Toán học, Kỹ thuật, Khoa học tự nhiên đang theo học môn Giải tích 1 hoặc các môn liên quan đến tích phân.
Nội dung tóm tắt
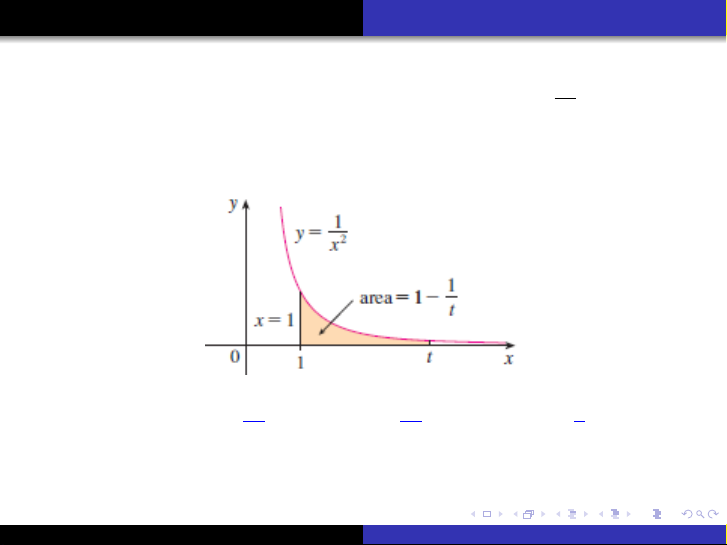
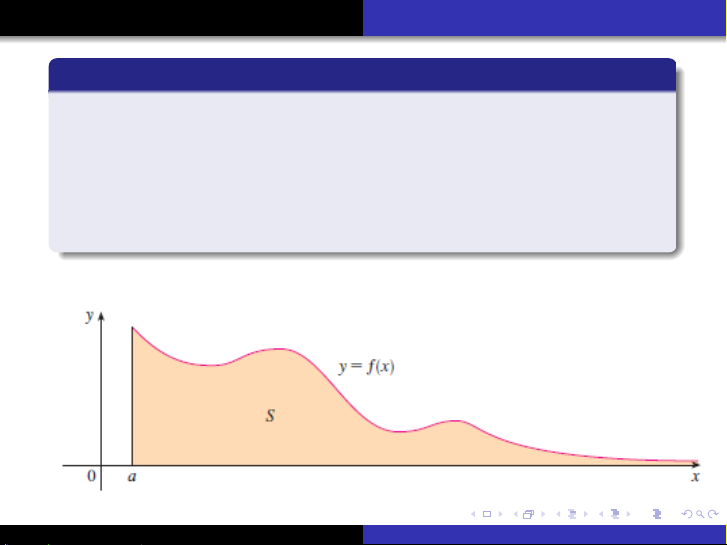
Tài liệu trình bày chi tiết về tích phân suy rộng, bao gồm định nghĩa và các loại tích phân suy rộng (loại I và loại II). Nội dung tập trung vào việc giải thích cách tính tích phân suy rộng thông qua giới hạn, đồng thời làm rõ khái niệm hội tụ và phân kỳ của chúng. Các ví dụ minh họa được cung cấp để giúp người đọc hiểu rõ hơn về cách áp dụng các định nghĩa và tiêu chuẩn hội tụ/phân kỳ trong thực tế. Đây là kiến thức nền tảng cho sinh viên ngành toán, kỹ thuật và các ngành khoa học tự nhiên.