Giới thiệu tài liệu
Tài liệu này giới thiệu một cách tổng quan về khái niệm tích phân xác định và tổng Riemann, bắt đầu từ việc đặt ra bài toán tính diện tích dưới đường cong.
Đối tượng sử dụng
Tài liệu này hướng đến sinh viên đang theo học các môn toán cao cấp như Giải tích 1 (Calculus 1), đặc biệt là những người cần nắm vững kiến thức về tích phân xác định và các ứng dụng cơ bản của nó trong các ngành khoa học tự nhiên và kỹ thuật.
Nội dung tóm tắt
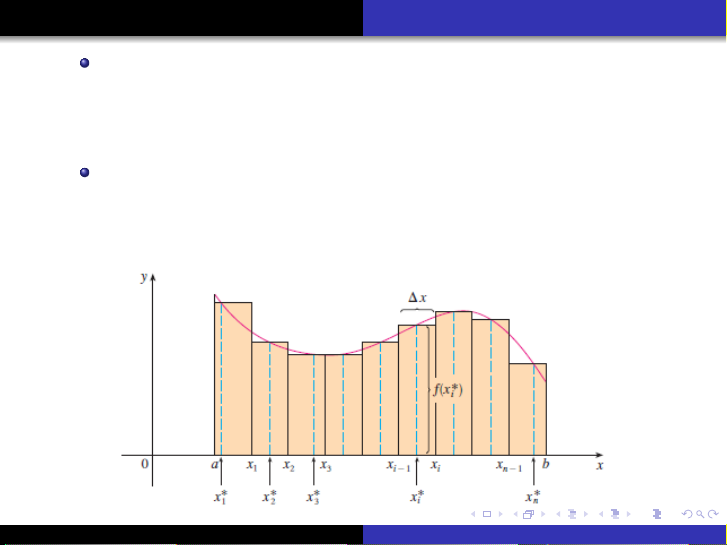
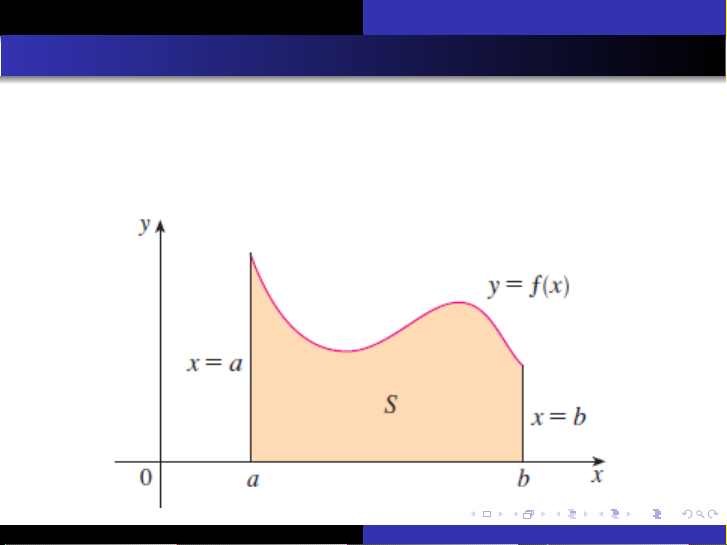
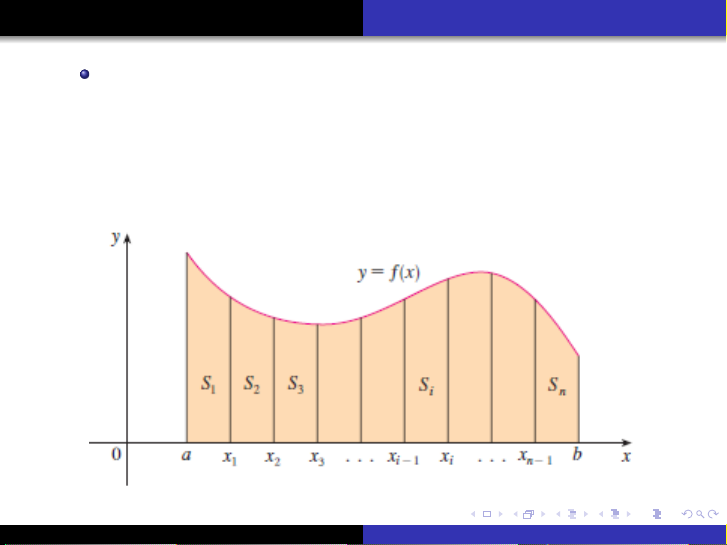
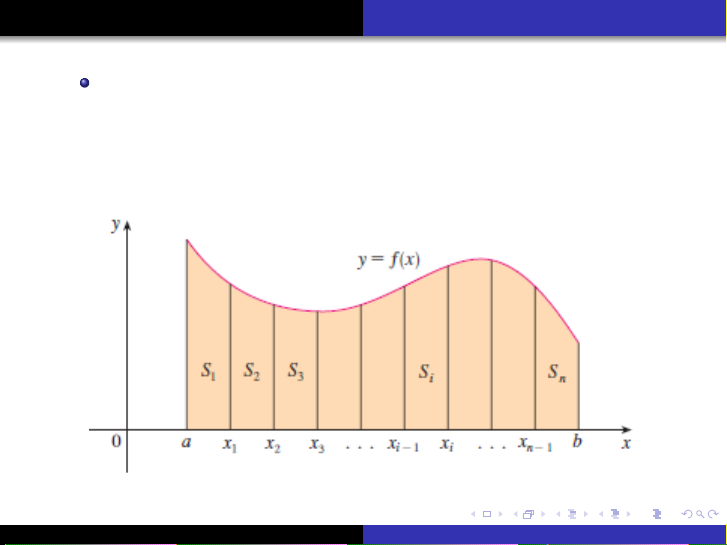
Tài liệu cung cấp một cái nhìn chi tiết và có hệ thống về tích phân xác định, khởi nguồn từ bài toán hình học cổ điển là tính diện tích của miền nằm dưới một đường cong (hình thang cong). Nó trình bày rõ ràng ý tưởng phân chia miền này thành các đoạn nhỏ hơn và xấp xỉ diện tích của từng đoạn bằng các hình chữ nhật, từ đó dẫn đến khái niệm tổng Riemann. Các loại tổng Riemann khác nhau, bao gồm tổng Riemann trái, phải và trung tâm, được giải thích thông qua việc lựa chọn điểm mẫu trong mỗi đoạn con. Định nghĩa chính thức của tích phân xác định được đưa ra như là giới hạn của tổng Riemann khi độ rộng của các đoạn con tiến về 0. Ngoài ra, tài liệu cũng đề cập đến khái niệm giá trị trung bình của hàm số, mặc dù trọng tâm chính của các trang được cung cấp là về tích phân xác định và tổng Riemann. Một ví dụ minh họa cụ thể với hàm số mũ f(x) = e^-x được sử dụng để làm rõ cách áp dụng tổng Riemann trong việc ước lượng diện tích.