KHUẾCH TÁN VÀ LÀM CHẬM
NEUTRON
Tham khảo chính: “Introduction to Nuclear
Engineering” của John R. Lamarsh
Nội dung
Mở đầu
Thông lượng Neutron
Định luật Fick
Phương trình liên tục
Phương trình khuếch tán
Điều kiện biên
Các nghiệm của phương trình khuếch tán
Độ dài khuếch tán
Phương pháp khuếch tán nhóm
Khuếch tán neutron nhiệt
Tính toán làm chậm neutron hai nhóm
Mở đầu
•Để thiết kế một lò phản ứng hạt nhân một cách đúng
đắn cần phải tiên đoán neutron phân bố như thế nào
trong hệ thống.
•Đây là một bài toán khó do lộ trình của các neutron là rất
phức tạp do kết quả của các va chạm hạt nhân liên tiếp.
•Một trong các phép gần đúng là coi neutron “khuếch tán”
(diffusion) như là một chất khí trong một chất khí khác.
•Phân bố neutron có thể tìm được bằng cách giải
phương trình khuếch tán.
•Cách làm này gọi là gần đúng khuếch tán và hiện nay
vẫn còn được dùng rộng rãi.
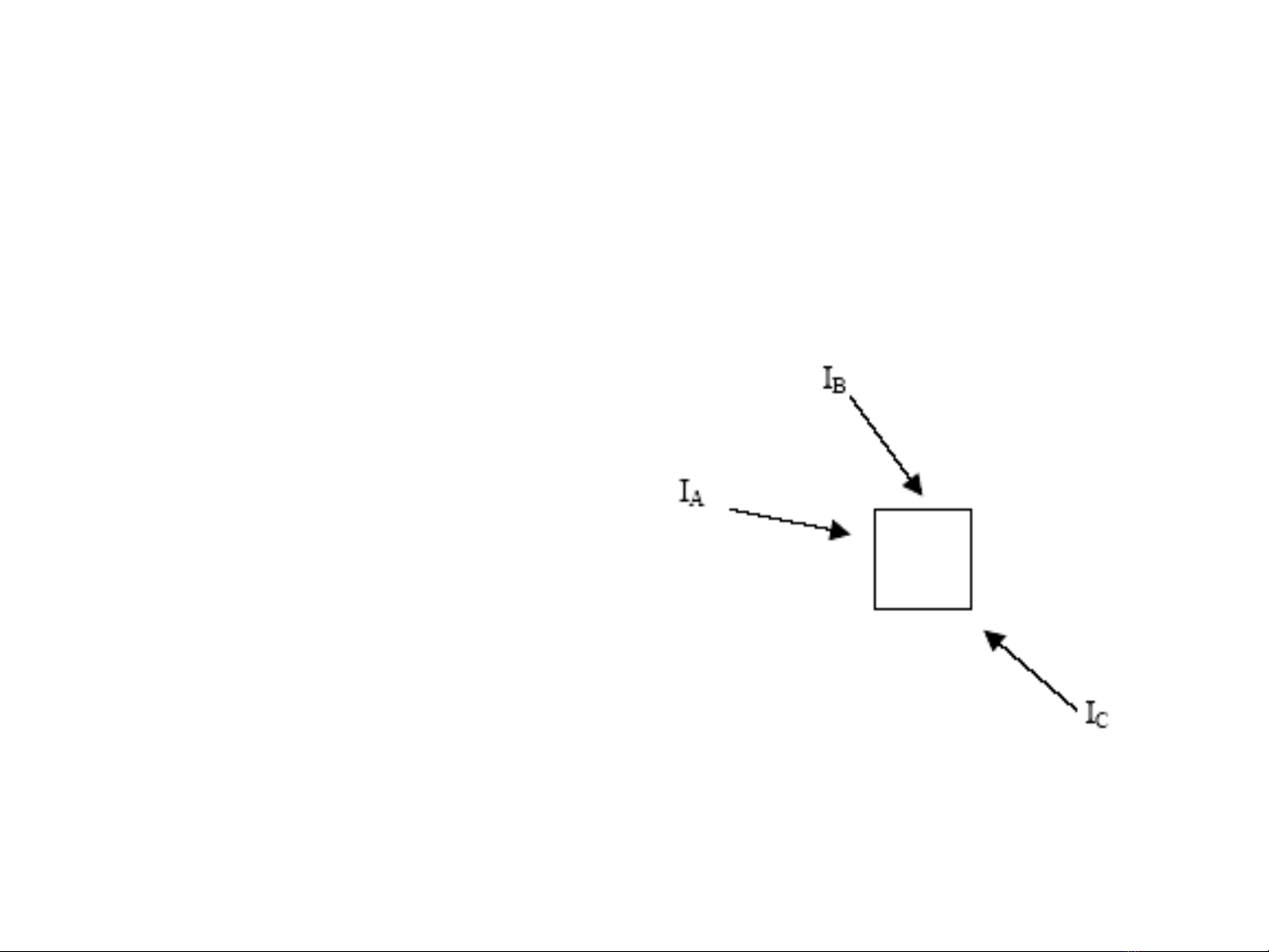
Thông lượng neutron (1)
IF t
...)(
CBAt
IIIF
vnnnF CBAt ...)(
nvF t
t
F
Số va chạm trên mỗi cm3/s khi một chùm neutron đi
vào một bia mỏng
Trường hợp có vài
chùm neutron
nv
là thông lượng neutron (flux) [cm-2.s-1]
Thông lượng neutron (2)
Dễ dàng mở rộng kết quả này cho các neutron có
một phân bố năng lượng
00
)()()()()( dEEEdEEvEnEF
tt
trong đó,
)()()( EvEnE
là thông lượng phụ thuộc năng lượng (energy-
dependent flux or flux per unit energy)
Phương trình trên là tốc độ tương tác tổng. Tốc độ
tương tác từng phần (tán xạ, hấp thụ) có thể xác
định bằng các biểu thức tương tự
0
)()( dEEEF
ss
0
)()( dEEEF
aa