Ch¬ng 1 Nh÷ng vÊn ®Ò c¬ b¶ncña khoa häc KTTNMT
KT häc tr¶ lêi c©u hái: lµm nh thÕ nµo trong c¸c quyÕt ®Þnh sö dông vµ ph©n phèi
nguån lùc con ngêi vµ nguån lùc tù nhiªn hiÖu qu¶ nhÊt.
-KT häc chia ra hai phÇn lµ KT vi m« vµ KT vÜ m«
-KTTNMT ra quyÕt ®Þnh thÕ nµo trong viÖc PT vµ qu¶n lý sö dông tµi nguyªn, MT
trong hiÖn t¹i vµ t¬ng lai.
•C¬ së lý thuyÕt cña KTTNMT
- Kh¸i niÖm: tËp hîp toµn bé c¸c ®Æc ®iÓm cña tµi nguyªn, hoÆc nguån tµi nguyªn mµ
c¸c ®Æc ®iÓm nµy x¸c lËp cho chñ së h÷u cña nã cã mét quyÒn lùc thùc sù ®Ó qu¶n lý,
vµ sö dông nã
- §Æc ®iÓm
+ QuyÒn së h÷u mét nguån tµi nguyªn cã thÓ bÞ giíi h¹n bëi chÝnh phñ;
+ Kho¶ng thêi gian khai th¸c lµ yÕu tè quan träng cho quyÒn së h÷u tån t¹i.
+ Chñ së h÷u cã nhiÒu quyÒn kh¸c nhau: Chñ së h÷u cã thÓ lo¹i trõ, cã thÓ tiÕn hµnh
c¸c ho¹t ®éng sö dông, cã thÓ chia vµ cã thÓ chuyÓn ®æi c¸c nguån tµi nguyªn.
+ Së h÷u chung
+ Tµi nguyªn v« chñ (Open acess)
•C¬ së KT vi m« vÒ phóc lîi x· héi
-C¸c ®iÒu kiÖn ®Ó ®¹t ®îc phóc lîi x· héi tèi ®a
(1) HiÖu qu¶ trong s¶n xuÊt
Gi¶ sö hµm s¶n xuÊt X = F (LX,KX) vµ Y = F (LY,KY)
r
w
MP
MP
MRTS
X
K
X
L
X
KL
==
®èi víi hµng ho¸ X
r
w
MP
MP
MRTS
Y
K
Y
L
Y
KL
==
®èi víi hµng ho¸ Y
(1)
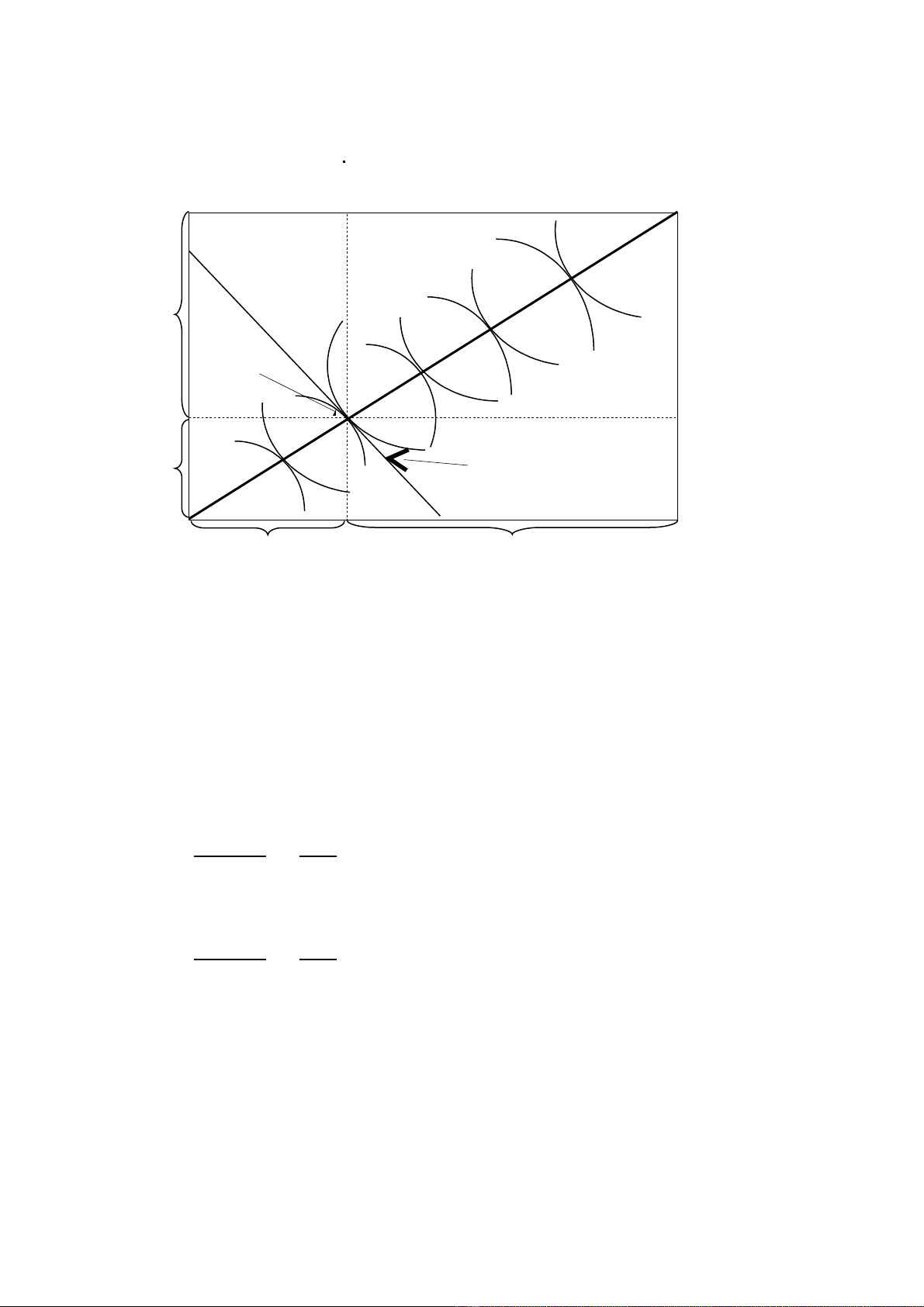
H×nh 1.1: HiÖu qu¶ trong s¶n xuÊt
-KÕt luËn
(2) HiÖu qu¶ trong qu¸ tr×nh tiªu dïng
Gi¶ sö hµm h÷u dông U = U (X,Y)
Y
X
A
Y
A
X
A
XY
P
P
MU
MU
MRS ==
®èi víi ngêi tiªu dïng A
Y
X
B
Y
B
X
B
XY
P
P
MU
MU
MRS ==
®èi víi ngêi tiªu dïng B
(2)
r
w
MRTSMRTS
Y
KL
X
KL
==
OY
OX
K
L
w/r
I1
I2
A
B
§êng ®ång
phÝ
LXLY
KX
KY
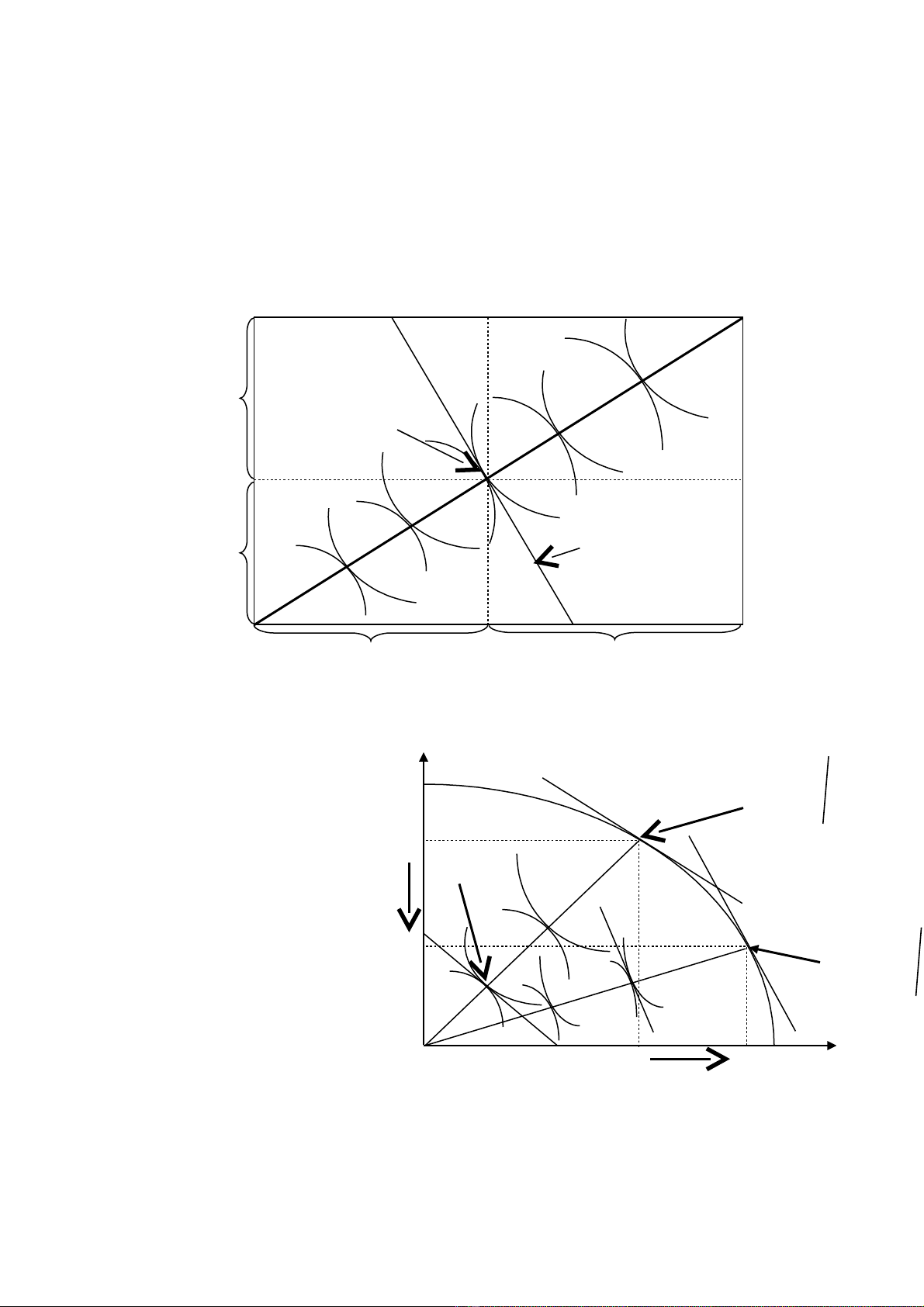
H×nh 1.2: HiÖu qu¶ trong tiªu dïng
KÕt luËn
(3) HiÖu qu¶ tæng hîp
Ta ®Æt:
XY
MRS
lµ MRS gi÷a hµng ho¸ X vµ Y
XY
MRT
tØ lÖ chuyÓn ®æi biªn cña hµng ho¸ X vµ Y
PP x¸c ®Þnh: HiÖu qu¶ trong ph©n phèi s¶n phÈm vµ tµi nguyªn ®¹t ®îc khi MRS gi÷a
hai lo¹i hµng ho¸ X vµ Y (MRSXY) b»ng víi tØ lÖ chuyÓn ®æi biªn (marginal rate of
transformation) gi÷a hai hµng ho¸ X vµ Y vµ b»ng víi tØ sè gi¸ gi÷ hai lo¹i hµng ho¸.
(3)
2
2
2
Y
X
XY
P
P
MRT
=
Y
A
1
1
1
Y
X
XY
P
P
MRT
=
B
MRSXY
Y1
Y2
X1X2
X
§êng ng©n s¸ch
A
B
Y
X
PX/PY
U1
U2
A
B
U3
XAXB
YA
YB
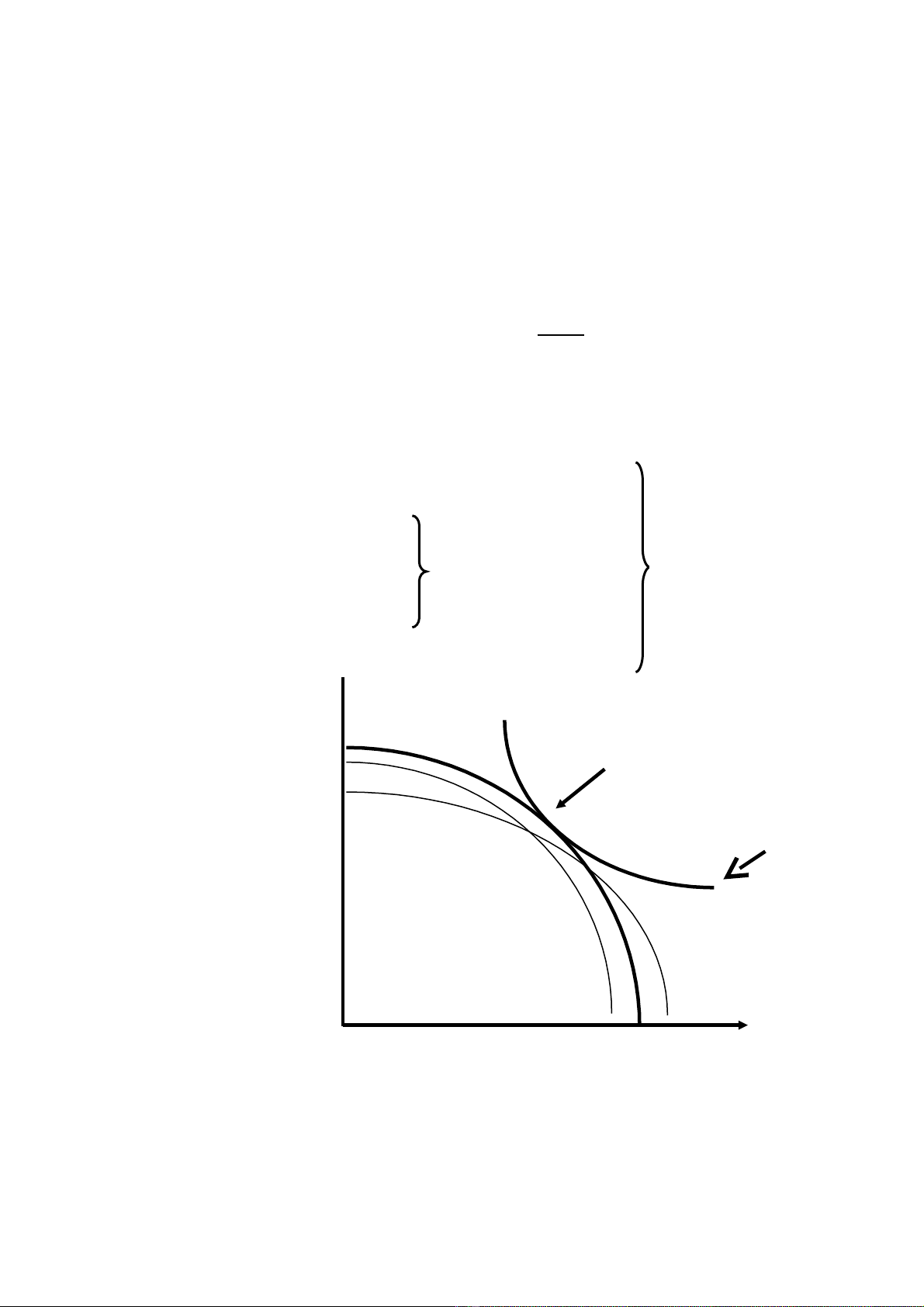
H×nh 1.3: HiÖu qu¶ hçn hîp (trong ph©n phèi)
KÕt luËn
(4) Tèi ®a ho¸ phóc lîi x· héi
§iÒu kiÖn ®Ó tèi ®a ho¸ phóc lîi x· héi
(1)HiÖu qu¶ trong s¶n xuÊt
(2)HiÖu qu¶ trong tiªu dïng Tèi u Pareto
(3)HiÖu qu¶ tæng hîp
(4) C«ng b»ng x· héi, lý thuyÕt cña sù chän lùa
Tèi ®a ho¸ phóc lîi x· héi
(5) Phóc lîi KT x· héi trong KTTN vµ vai trß cña chÝnh phñ
(4)
Y
X
XYXY
P
P
MRTMRS
==
Tèi
®a
ho¸
phóc
lîi x·
héi
§êng
phóc lîi
xa héi
SWF
Tèi ®a ho¸ phóc lîi
x· héi “Bliss point”
UA
UB
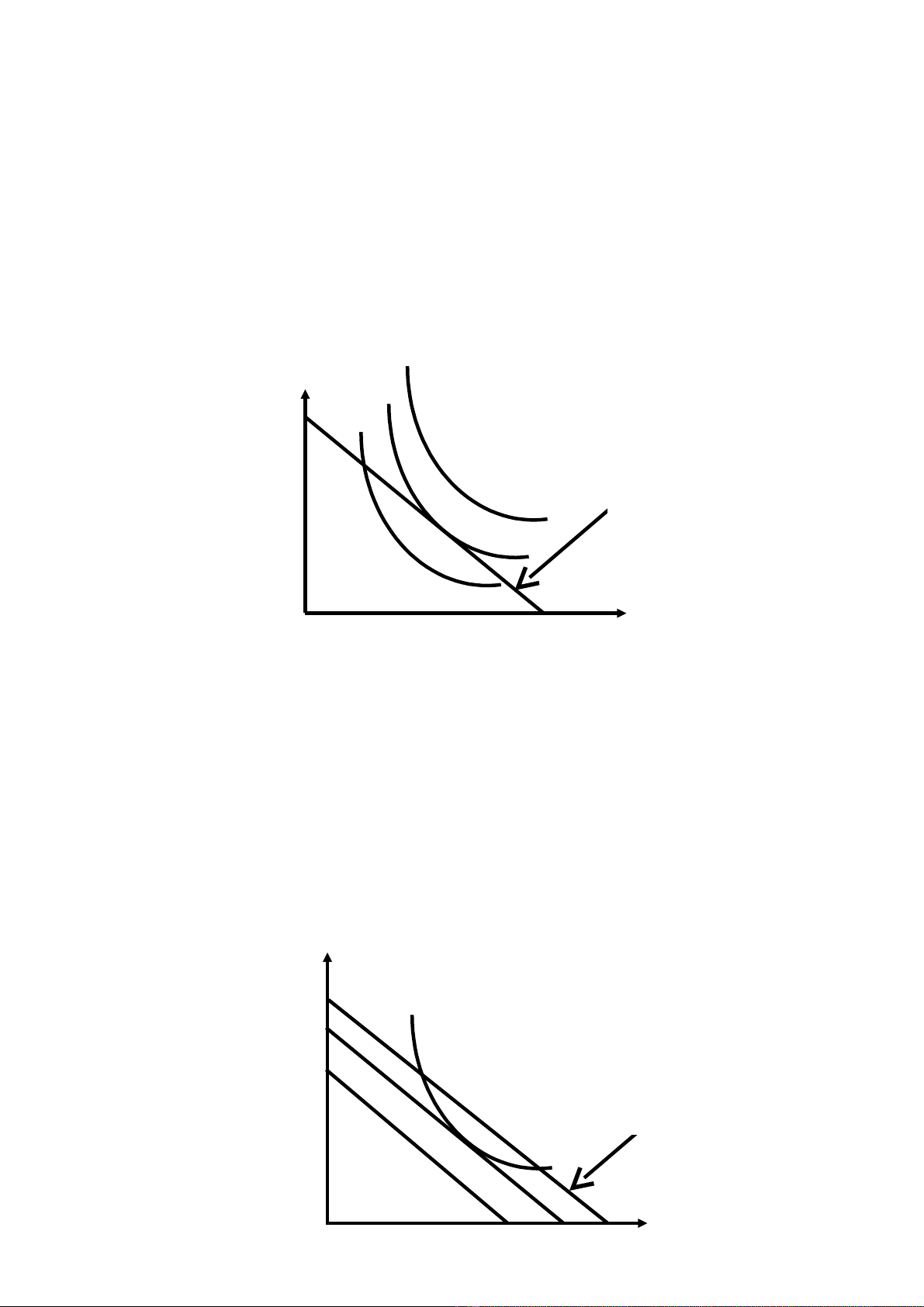
Tèi ®a ho¸ phóc lîi x· héi (Pareto optimal): Sö dông c¸c nguån tµi nguyªn (con ngêi, tù
nhiªn) trong mét nÒn KT ®· ®¹t tíi møc tèi u, mµ ë ®ã chØ cã thÓ t¨ng phóc lîi cña c¸
nh©n nµy trong x· héi b»ng con ®êng duy nhÊt lµ gi¶m phóc lîi cña c¸ nh©n kh¸c trong x·
héi.
1) Hµm cÇu Marshallian: Max U = U(Xi)
Rµng buéc: Y = ∑PiXi (rµng buéc vÒ ng©n s¸ch)
Trong ®ã: U lµ møc ®é tho¶ m·n (hµm h÷u dông),
Y lµ thu nhËp (ng©n s¸ch),
Xi lµ hµng ho¸ tiªu dïng i, Pi lµ gi¸ cña hµng ho¸, dÞch vô i
(2) Hµm cÇu Hicksian (hµm cÇu ®Òn bï)
Min Y = ∑PiXi
Rµng buéc: U = Uo(Xi)
Trong ®ã: U lµ møc ®é tho¶ m·n (hµm h÷u dông),
Y lµ thu nhËp (ng©n s¸ch),
Xi lµ hµng ho¸ tiªu dïng i, Pi lµ gi¸ cña hµng ho¸, dÞch vô i
(5)
q2
q1
®êng ng©n s¸ch
M« h×nh hµm Mars hallia
0
®êng ng©n
s¸ch
U0
q1
0
M« h×nh hµm Hic ks ian
q2