TR NG Đ I H C BÁCH KHOA TP.HCMƯỜ Ạ Ọ
B MÔN Đ A TIN H CỘỊỌ
CH NG 0ƯƠ
Gi I THI U MÔN H CỚ Ệ Ọ
Môn h c cung c p cho sinh viên các ki n th c:ọ ấ ế ứ
H th ng quy chi u tr c đ a Vi t Namệ ố ế ắ ị ệ
2
Công tác thi t k l i kh ng ch t a đô, cao ế ế ướ ố ế ọ
đ nhà n cộ ướ
Áp d ng các k thu t đo góc, đo dài, đo cao ụ ỹ ậ
chính xác vào công tác l p l i kh ng chậ ướ ố ế
Tính toán s li u đo đ c, bình sai l i kh ng ố ệ ạ ướ ố
ch t a đ , cao đế ọ ộ ộ
Tính toán giá thành xây d ng l i, t ch c thi ự ướ ổ ứ
công l i kh ng chướ ố ế
Ch ng 1: H QUY CHI U VÀ L I TR C Đ Aươ Ệ Ế ƯỚ Ắ Ị
•H quy chi u:ệ ế g c to đ và h tr c c s to đ ố ạ ộ ệ ụ ơ ở ạ ộ
đ d a vào đó có th bi u di n đ c t t c các đi m ể ự ể ể ễ ượ ấ ả ể
trong không gian.
•L i tr c đ aướ ắ ị là m t t p h p các đi m c s đã xác ộ ậ ợ ể ơ ở
đ nh to đ – đ cao trong h quy chi u có đ chính ị ạ ộ ộ ệ ế ộ
xác theo yêu c u, đ c b trí v i m t đ phù h p ầ ượ ố ớ ậ ộ ợ
trên ph m vi lãnh th đang xét ạ ổ
•Các lo i h quy chi u:ạ ệ ế
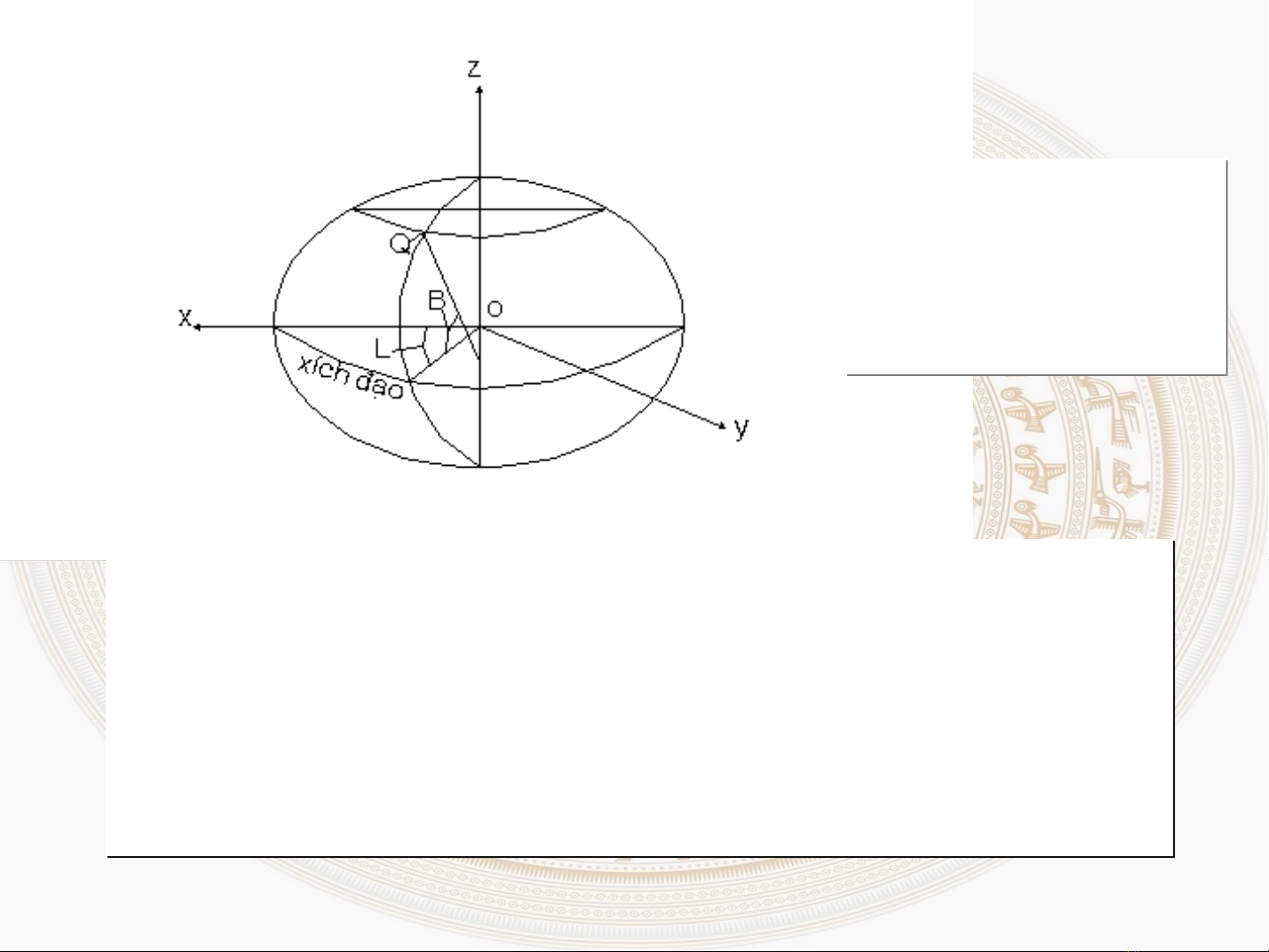
–H quy chi u vuông góc không gian X, Y, Z ệ ế
–H quy chi u m t ellipsoid B,L,Hệ ế ặ
–H quy chi u m t b ng x,y s d ng ch y u cho m c đích ệ ế ặ ằ ử ụ ủ ế ụ
thành l p các lo i b n đ .ậ ạ ả ồ
3
Cách th c thành l p h quy chi u ứ ậ ệ ế
và l i tr c đ aướ ắ ị
1. Đo đ c m t l i các đi m to đ c s (h to đ ) ạ ộ ướ ể ạ ộ ơ ở ệ ạ ộ
b ng các th lo i công ngh đ t đ chính xác cao ằ ể ạ ệ ạ ộ
nh t và có m t đ theo yêu c u.ấ ậ ộ ầ
2. Xác đ nh đ c h quy chi u phù h p trên c s ị ượ ệ ế ợ ơ ở
ch nh lý các k t qu đo h to đ các đi m c s .ỉ ế ả ệ ạ ộ ể ơ ở
3. Ch nh lý các k t qu đo h to đ các đi m c s ỉ ế ả ệ ạ ộ ể ơ ở
trong h quy chi u đã xác đ nh.ệ ế ị
4. H to đ các đi m c s t o thành m t l i đi m ệ ạ ộ ể ơ ở ạ ộ ướ ể
làm g c t ng đ i v i xác đ nh các đi m to đ khác ố ươ ố ớ ị ể ạ ộ
quanh nó.
4
Kinh đ tr c đ a ộ ắ ị L
Vĩ đ tr c đ a ộ ắ ị B
Cao đ tr c đ a ộ ắ ị H
Kinh đ tr c đ a ộ ắ ị L
Vĩ đ tr c đ a ộ ắ ị B
Cao đ tr c đ a ộ ắ ị H
Quan h gi a to đ tr c đ a ệ ữ ạ ộ ắ ị B, L và thiên văn
ϕ
,
λ
Quan h gi a to đ tr c đ a ệ ữ ạ ộ ắ ị B, L và thiên văn
ϕ
,
λ
( )
( )
.cos
2sin171".0
BL
BHB
km
−=
−−=
λη
ϕξ
5
