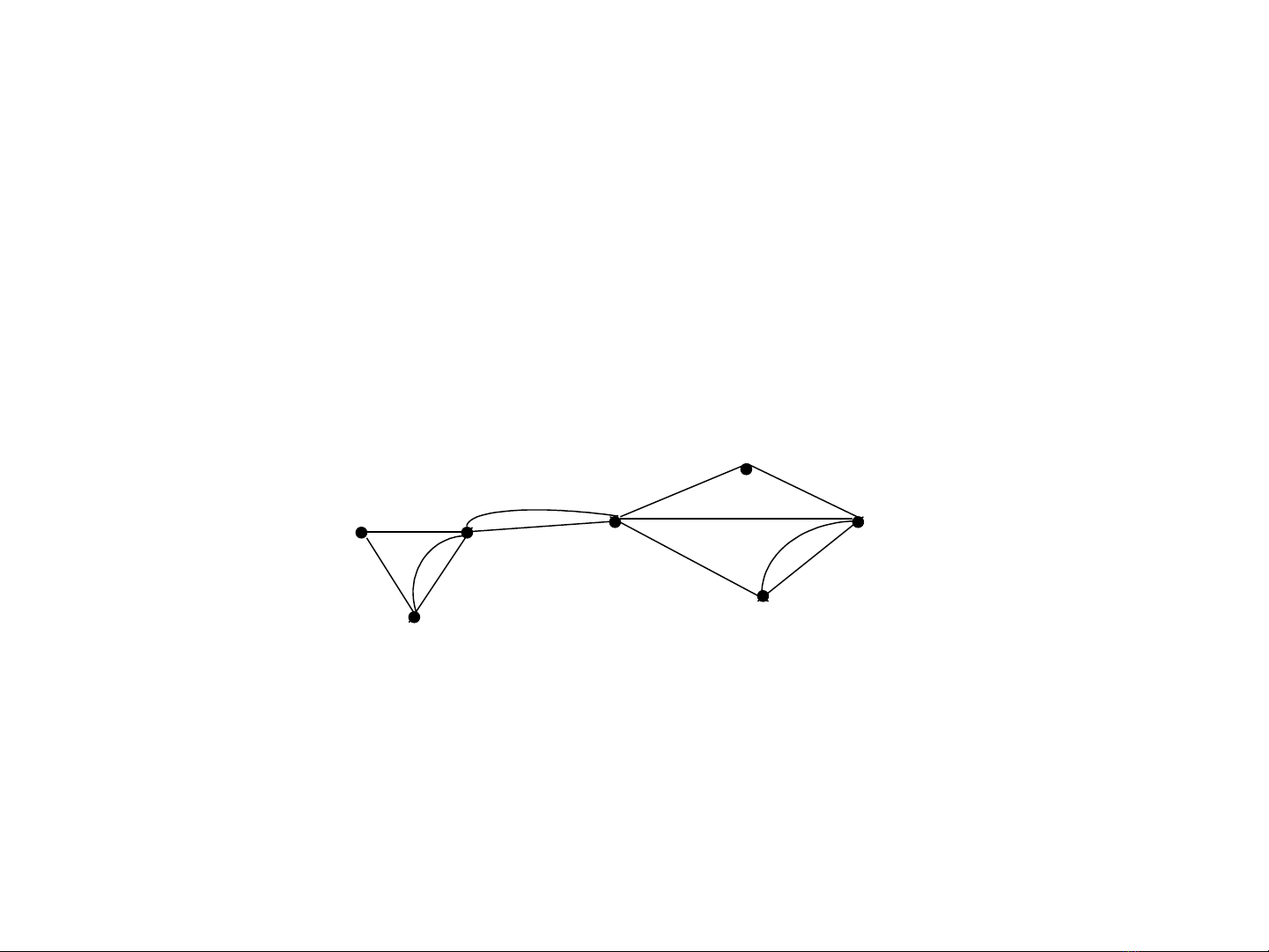
Đ n đ th , đa đ thơ ồ ị ồ ị
•Đ th ồ ị G = (V,E) g i là ọđa đ thồ ị n u nó có ế
ít nh t m t c p đ nh đ c n i v i nhau ấ ộ ặ ỉ ượ ố ớ
b i hai c nh tr lên và không có khuyênở ạ ở
C1
C3
C2
C4
C5
C7
C6
m ng này có nhi u kênh tho i n i gi a hai Ở ạ ề ạ ố ữ
máy. Mô hình m ng trên là m t đa đ th .ạ ộ ồ ị
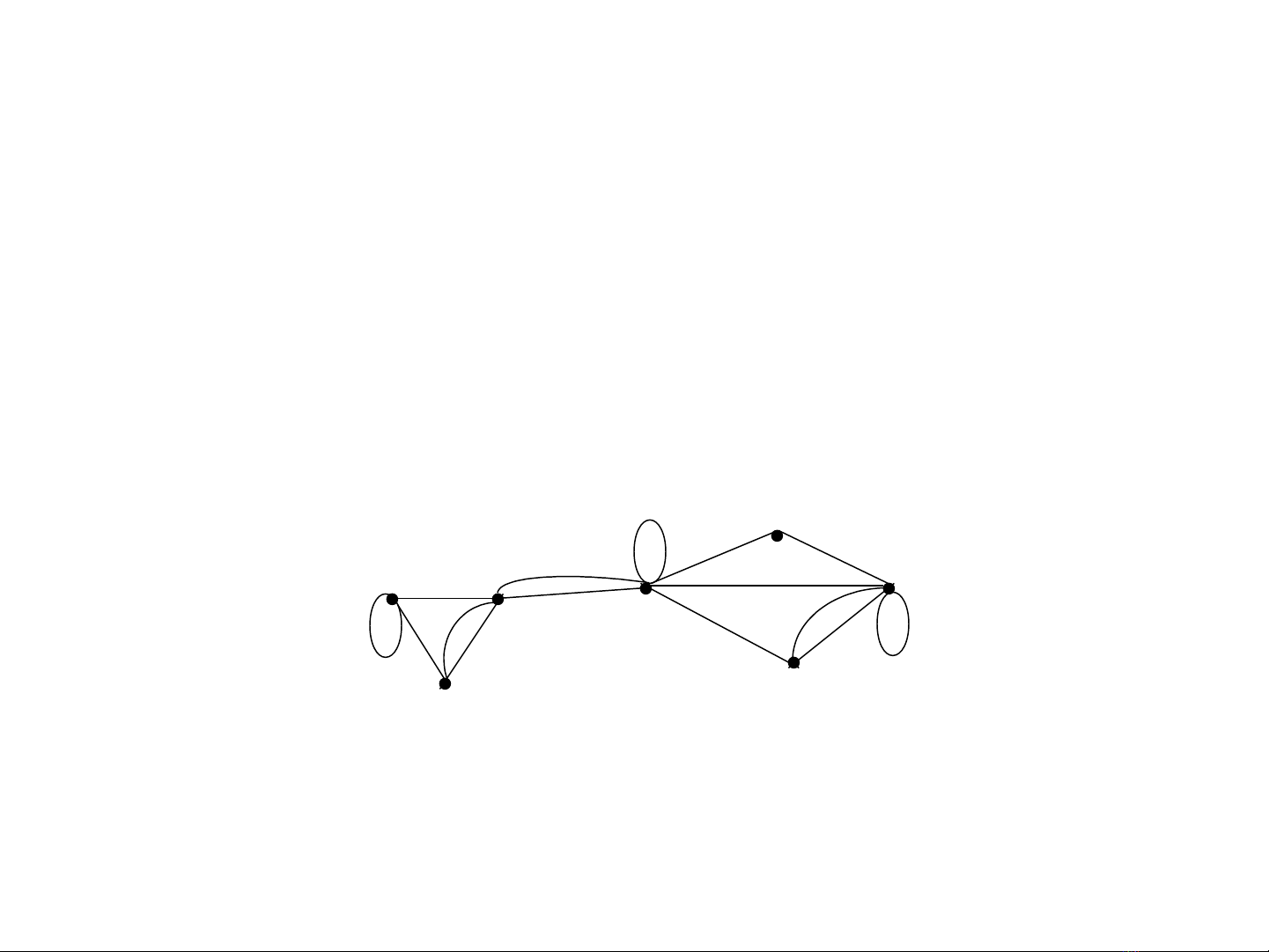
Gi đ thả ồ ị
Gi đ th vô h ngả ồ ị ướ G=(V,E) bao g m V là ồ
t p các đ nh, E là t p các c p không có th t ậ ỉ ậ ặ ứ ự
g m hai ph n t (không nh t thi t khác nhau) ồ ầ ử ấ ế
c a V g i là các c nh.ủ ọ ạ
•Các e đ c g i là khuyên n u có d ng ượ ọ ế ạ
e=(u,u)
•Ví d : ụC1
C3
C2
C4
C5
C7
C6
M ng máy tính có đ ng đi n tho i t m t máy ạ ườ ệ ạ ừ ộ
tính đ n chính nó. Mô hình trên là m t gi đ th ế ộ ả ồ ị
vô h ng.ướ
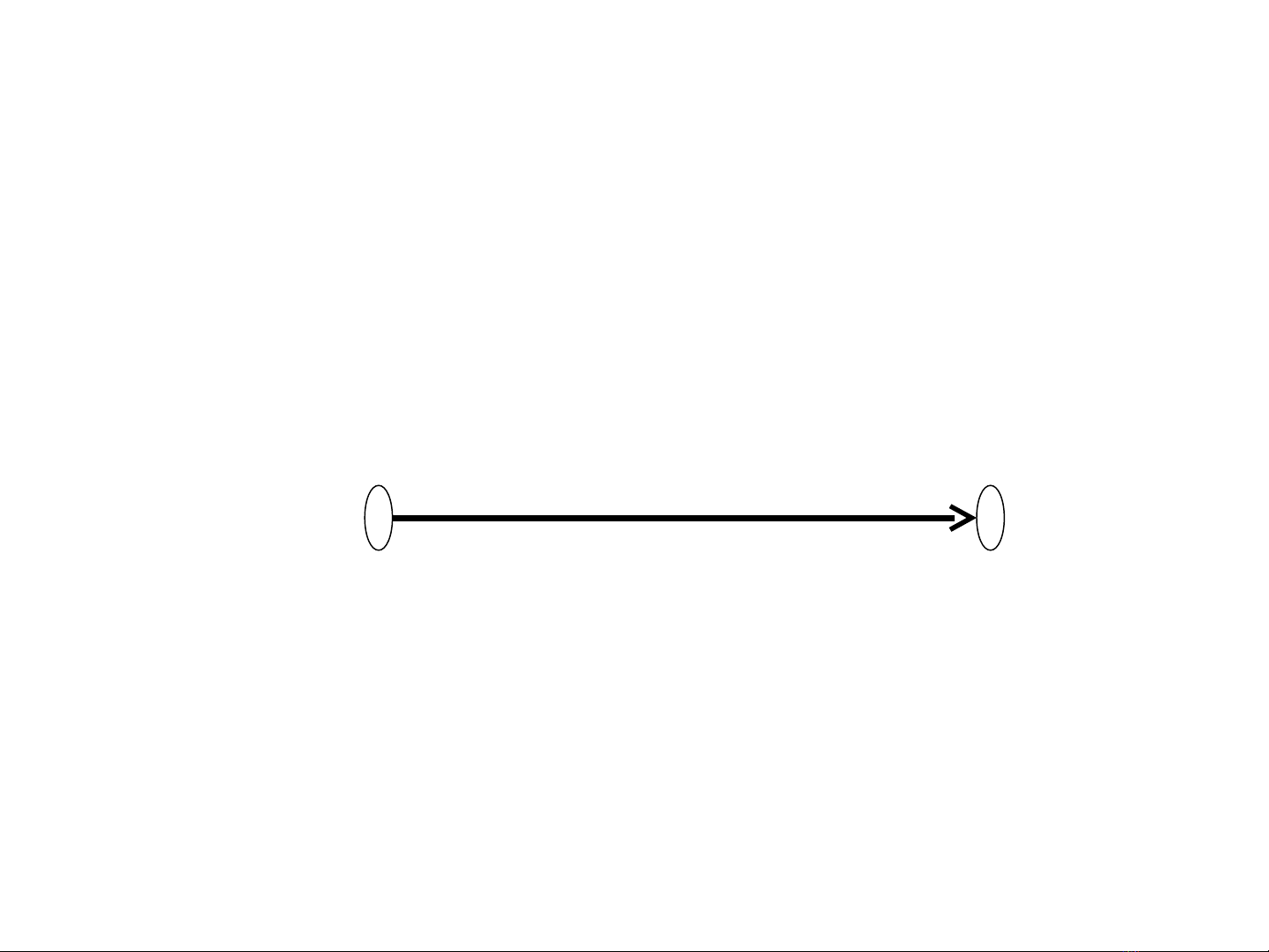
Lý thuy t đ thế ồ ị 3
Đ th có h ngồ ị ướ
G = (V,E) là đ th có h ngồ ị ướ n u v i m i ế ớ ọ
c nh e=(x,y) ạ∈ E có phân bi t th t các ệ ứ ự
đ nh x và y, có h ng x đ n y, hay ỉ ướ ế
(x,y) ≠ (y,x)
Đ i v i m t cung e = (x, y):ố ớ ộ
•x là đ nh đi (g c,đ u)ỉ ố ầ
•y là đ nh đ n(ng n, cu i)ỉ ế ọ ố
•Cung e đi t x và đ n yừ ế
xy
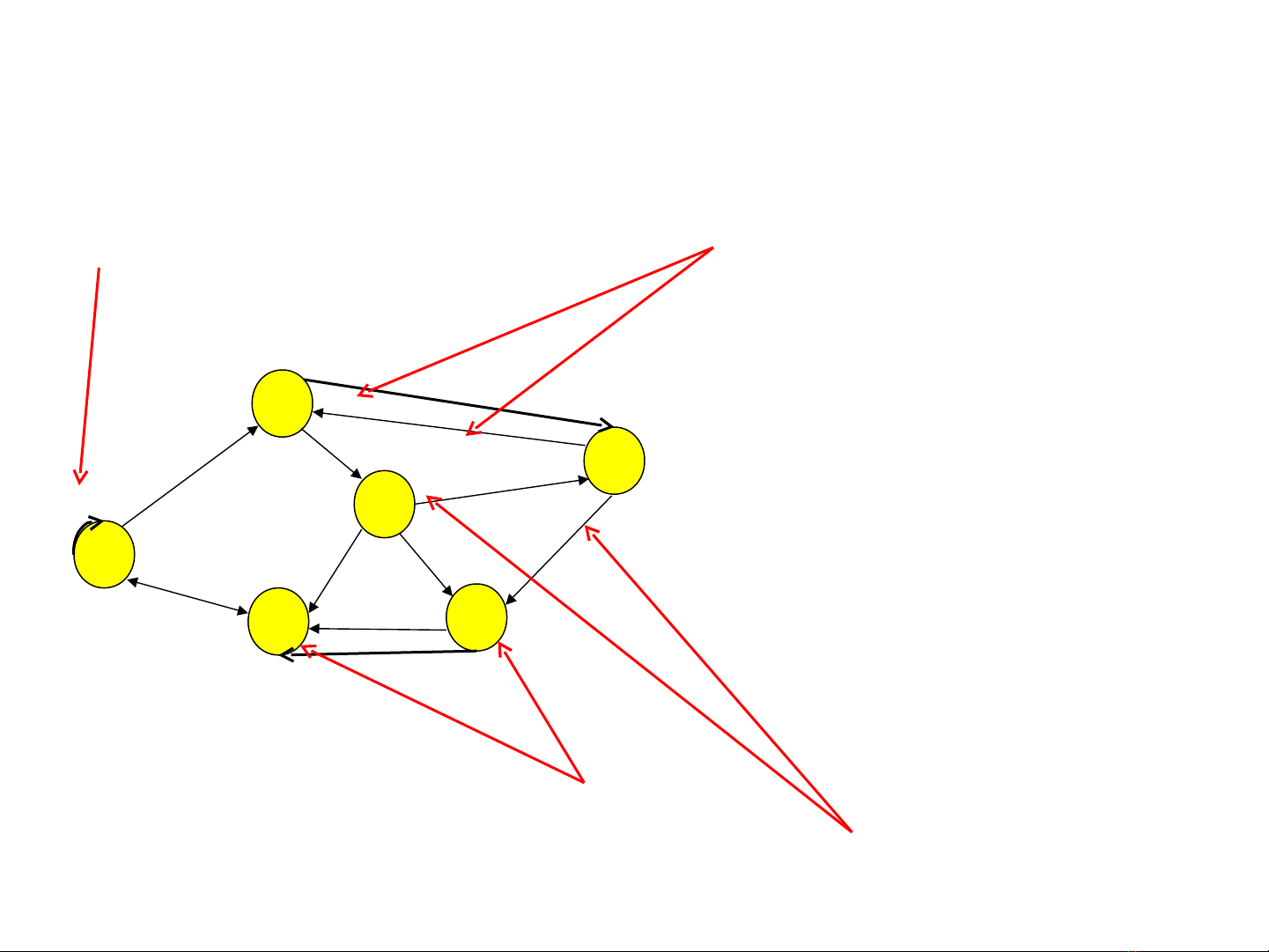
Lý thuy t đ thế ồ ị 4
Đ th có h ngồ ị ướ
1
4
3
6
5
2
G = (V, E)
V = {1, 2, 3, 4, 5, 6}
E = { (1,4), (1,6), (2,1), (2,3),
(3,2), (4,3), (4,5), (4,6), (5,3),
(6,1), (6,5),(5,3)}
(1, 4) = 1→4
Khuyên Song song
C nh Kạ ề
Đ nh Kỉ ề
Đ th có h ngồ ị ướ
•Cho G=(V,E) la môt đô thi co h ng va ươ
e=(vi,vj)∈E :
–vj đ c g i là ượ ọ đinh sau c a vủi
–vi la môt đinh tr c ươ cua v j
•T p các đ nh sau va đinh tr c c a vậ ỉ ươ ủ i lân
l t đ c ki hiêu la ươ ươ Γ (vi) va Γ-1(vi)
Γ (x) = {y ∈ V | (x,y) ∈E}
•G=(V,E) = (V, Γ)
Lý thuy t đ thế ồ ị 5