Giới thiệu tài liệu
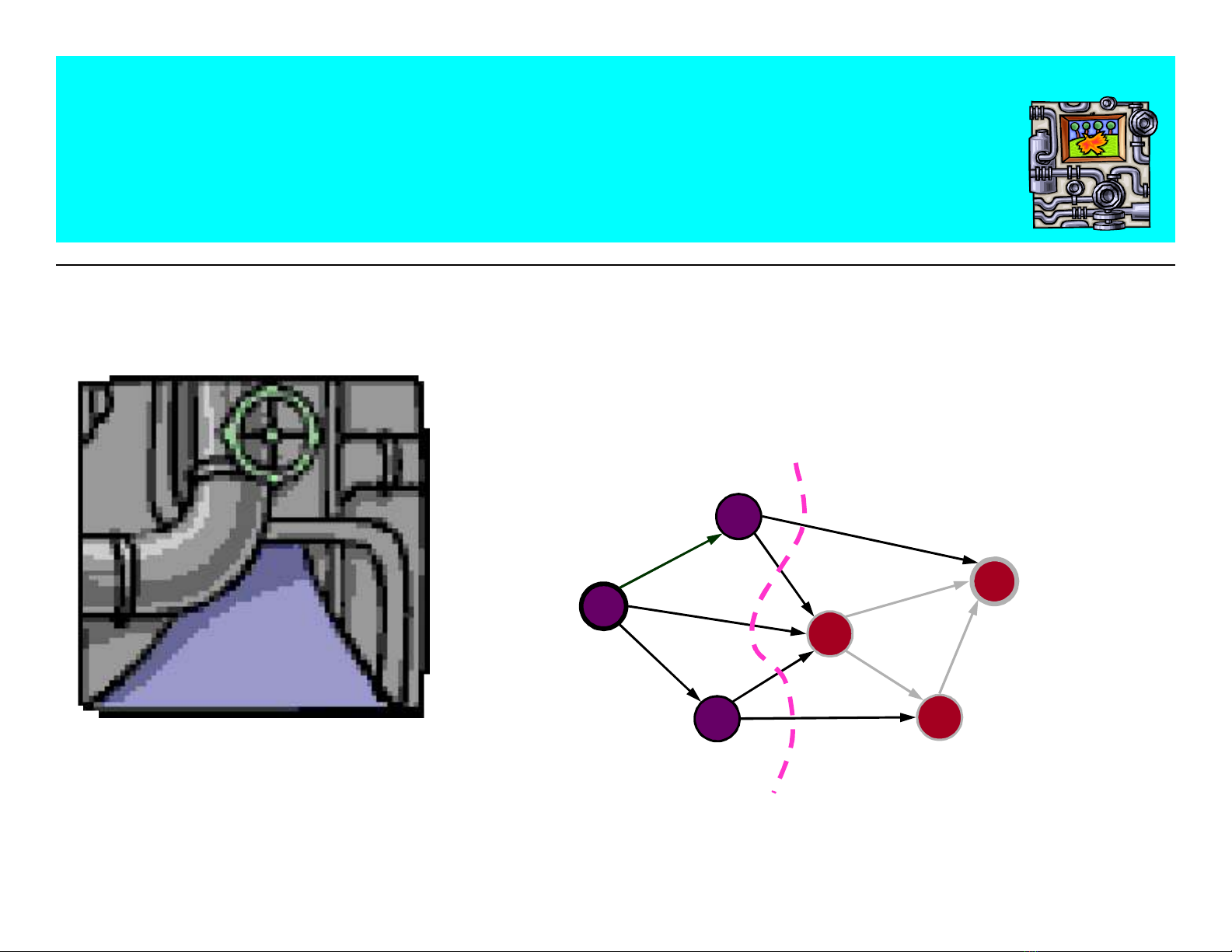
Chương 6: Bài toán luồng cực đại là một bài giảng học thuật trong lý thuyết đồ thị, cho biết các kiến thức về bài toán luồng cực đại trong mạng, luồng trong mạng, thuật toán Ford-Fulkerson và các ứng dụng của lý thuyết đồ thị trong nhiều lĩnh vực khác nhau.
Đối tượng sử dụng
Nhà nghiên cứu, sinh viên học lý thuyết đồ thị, những người có quan tâm đến các bài toán phân tích và đề xuất trong nhiều lĩnh vực khác nhau.
Nội dung tóm tắt
Bài giảng Lý thuyết đồ thị - Chương 6: Bài toán luồng cực đại cung cấp cho người đọc những kiến thức về bài toán luồng cực đại trong mạng, bao gồm định nghĩa, các điều kiện, phép tính và các thuật toán được sử dụng để giải quyết bài toán luồng cực đại. Bài giảng chỉ ra rõ rằng lý thuyết đồ thị là một công cụ hữu ích để giúp cho việc phân tích và đề xuất cho nhiều bài toán trong nhiều lĩnh vực khác nhau, bao gồm truyền thông, tài chính, giao thông và hóa học. Ngoài ra, bài giảng cũng giới thiệu định lý về luồng cực đại và lát cắt hẹp nhất, thuật toán Ford-Fulkerson và Edmond-Karp. Bài giảng cho biết rằng bài toán luồng cực đại là một bài toán không dễ dàng nhưng nó có nhiều ứng dụng và nó là một trong những công cụ hữu ích để giúp cho việc phân tích và đề xuất cho nhiều bài toán trong nhiều lĩnh vực.