Chương 4
ĐỒ THỊ EULER
và ĐỒ THỊ HALMITON
2
26/03/2011
4.1 Đồ thị Euler
Lý thuyết đồ thị
Định nghĩa
Xét đồ thịG=(V,E)
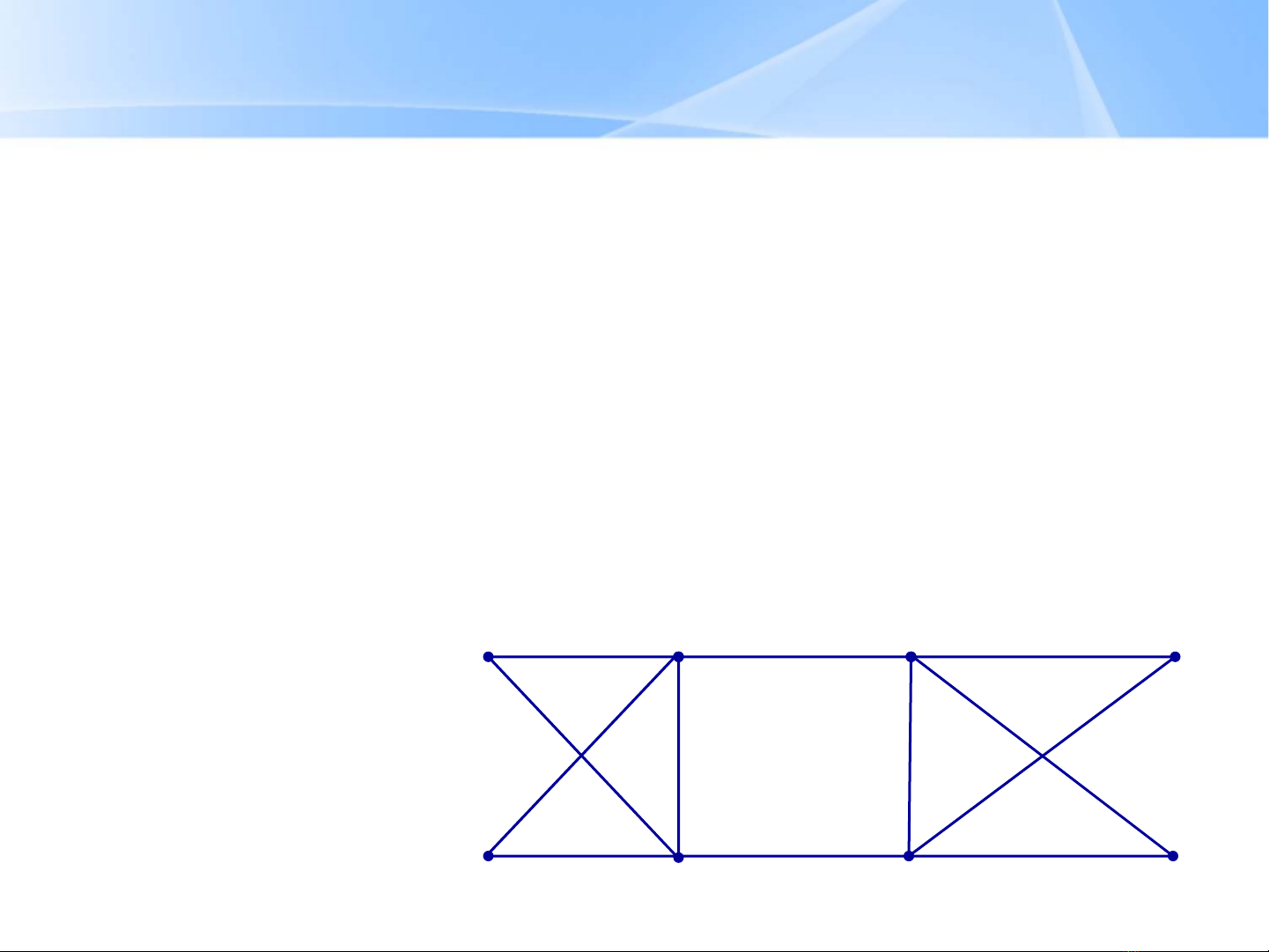
–Đường điđơn trong G đượcgọilàđường điEulernếu
nó đi qua tấtcảcác cạnh, mỗicạnh mộtlần.
–Chu trình đơn trong G đượcgọilàchu trình Euler nếu
nó đi qua tấtcảcác cạnh, mỗicạnh mộtlần.
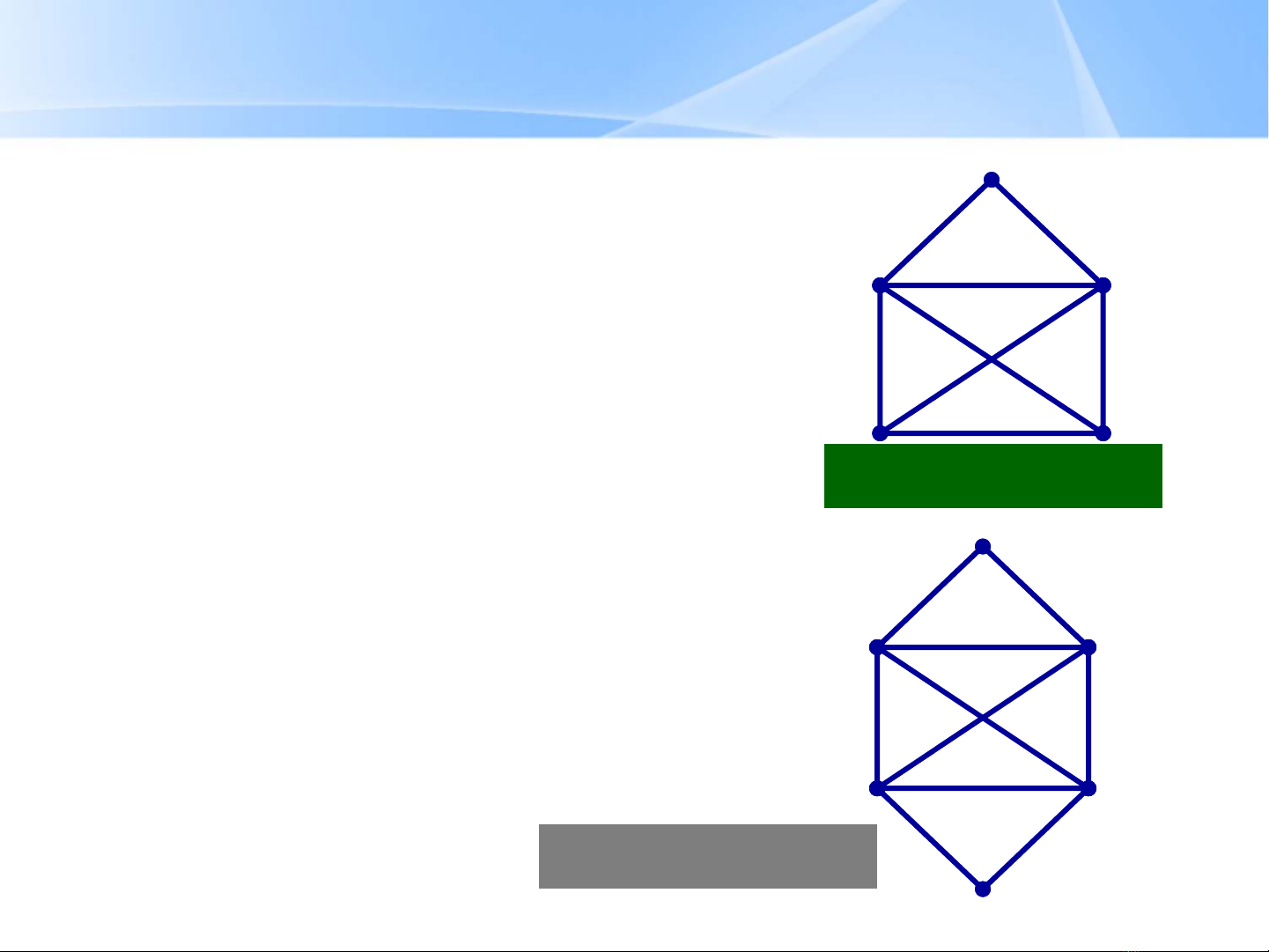
–Đồ thịGđượcgọilàđồ thịEuler nếu có chu trình Euler.
–Đồ thịGđượcgọilàđồ thịnửaEulernếucóđường đi
Euler.
3
26/03/2011
4.1 Đồ thị Euler
Lý thuyết đồ thị
Ví dụ:
Đồ thịG1có các đường điEulerlà:
d1:123425415
d2:124325145
…
Đồ thị G2có các chu trình Euler là:
C1: 1 2 3 4 2 5 4 1 5 6 1
C2: 1 2 4 3 2 5 1 4 5 6 1
…
1
2
3
4
5
G1
1
2
3
4
5
6
G2
Đồ thị nửa Euler
Đồ thị Euler
4
26/03/2011
4.1 Đồ thị Euler
Lý thuyết đồ thị
Định lý 1
Đồ thịvô hướng liên thông G là đồ thịEuler khi và chỉ
khi mọiđỉnh củaGđềucóbậcchẵn.
Hệquả
Đồ thịvô hướng liên thông G là đồ thịnửa Euler khi và
chỉkhi nó có không quá 2 đỉnh bậclẻ.
5
26/03/2011
4.1 Đồ thị Euler
Lý thuyết đồ thị
Thuật toán Fleury xác định chu trình Euler
Xuấtpháttừmộtđỉnh bấtkỳcủaG,đitheocáccạnh
một cách tùy ý, chỉcầntuânthủhai quy tắcsau:
i) Xóa bỏcạnh đãđi qua và đồng thờixóacảnhững đỉnh
cô lậptạo thành.
ii) Ởmỗibước, chỉđiquacầu khi không còn cách chọnlựa
nào khác.
Ví dụ:
Tìm chu trình ởEuler
trong đồ thị
a b c d
e
fgh
