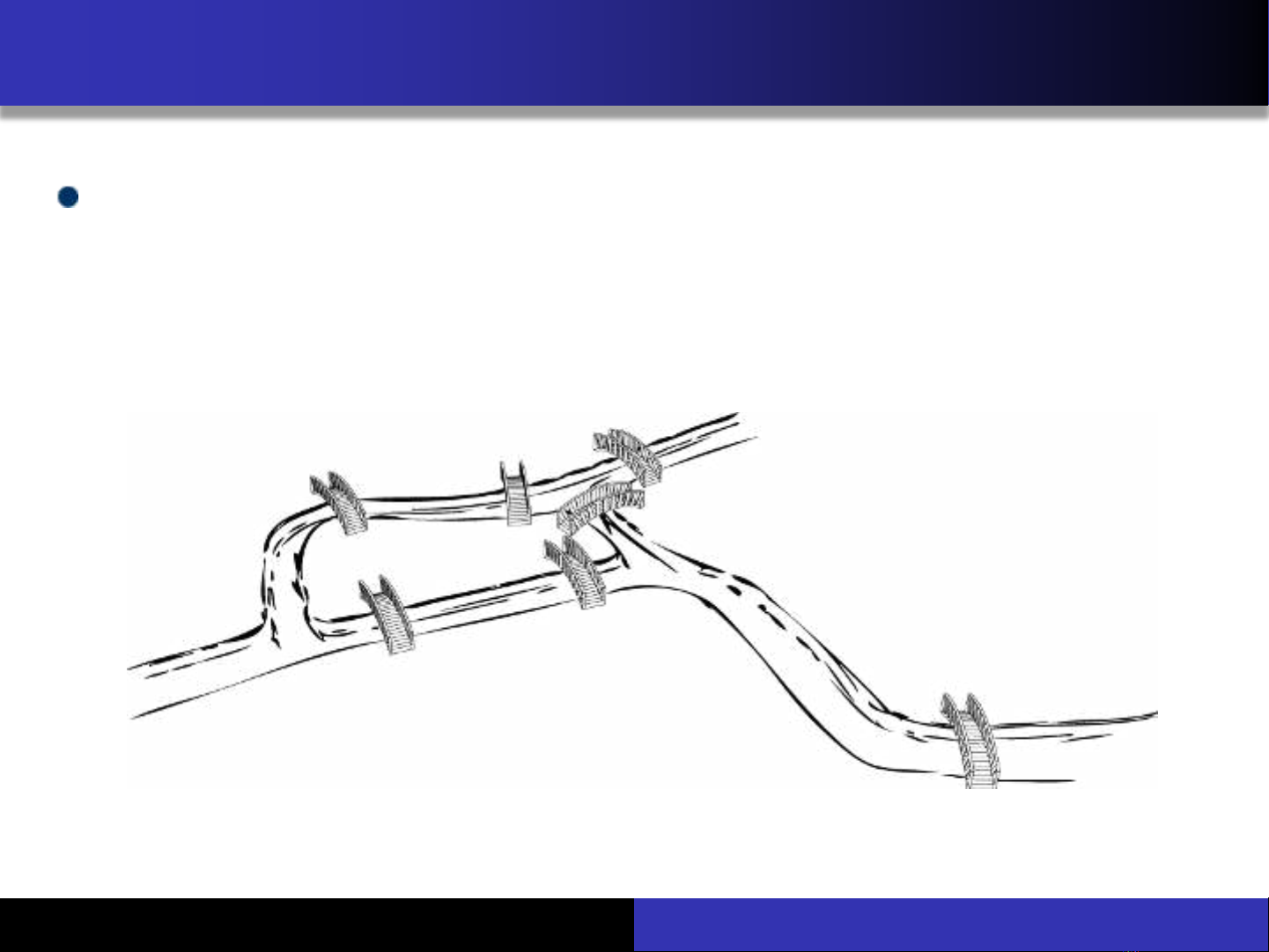
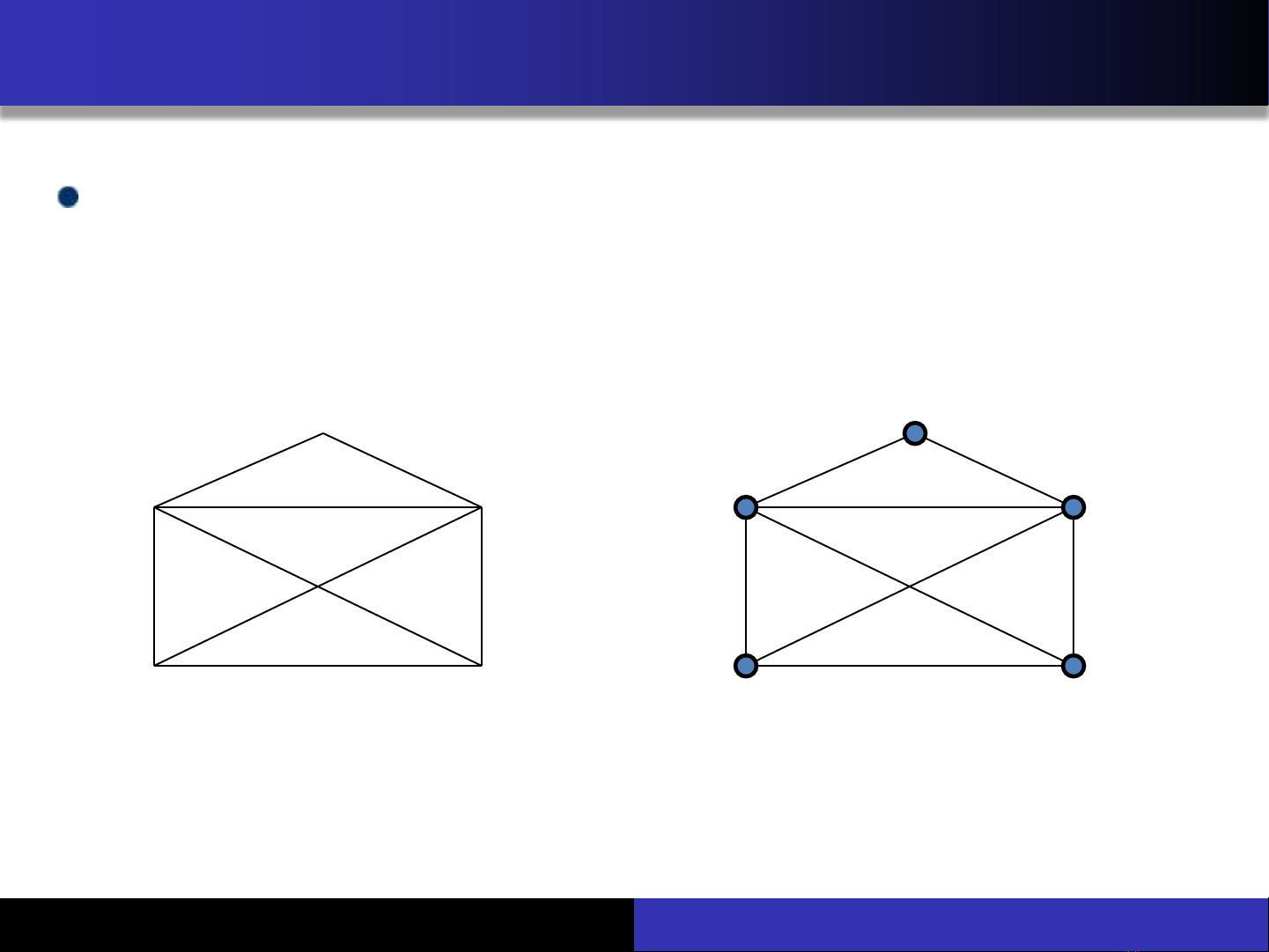
Giới thiệu tài liệu
Bài giảng Lý thuyết đồ thị: Chương 1 - Tôn Quang Toại là một tài liệu giúp học viên nắm bắt các kiến thức cơ bản về lý thuyết đồ thị, chẳng hạn như định nghĩa, phân loại, ký hiệu và các thuật ngữ cơ bản.
Đối tượng sử dụng
Sinh viên học lý thuyết đồ thị
Nội dung tóm tắt
Bài giảng Lý thuyết đồ thị: Chương 1 - Tôn Quang Toại là một tài liệu học thuật, mình sẽ giới thiệu các bài toán dẫn đến khái niệm đồ thị. Sau đó, tài liệu sẽ quảng cáo định nghĩa về đồ thị và phân loại đồ thị dựa trên hướng của cạnh và số cạnh nối 2 đỉnh. Ngoài ra, tài liệu cũng cung cấp ký hiệu đồ thị và các thuật ngữ cơ bản để học viên trở nên tự do hơn trong việc học lý thuyết đồ thị.