Bài giảng Ngôn ngữ hình thức: Chương 5 - Nguyễn Thị Hồng

Chia sẻ: _ _ | Ngày: | Loại File: PPT | Số trang:25

Thêm vào BST

Báo xấu

12
lượt xem 3
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng Ngôn ngữ hình thức: Chương 5 Máy turing và ôtômát tuyến tính giới nội, cung cấp cho người học những kiến thức như: Ngôn ngữ cảm ngữ cảnh; Ô tô mát tuyến tính giới nội; Sự tương đương giữa ô tô mát tuyến tính giới nội và văn phạm cảm ngữ cảnh. Mời các bạn cùng tham khảo!

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Ngôn ngữ hình thức: Chương 5 - Nguyễn Thị Hồng

MÁY TURING VÀ Ô TÔ MÁT TUYẾN TÍNH GIỚI NỘI
Nội dung  Máy turing tiền định  Ngôn ngữ ngữ cấu (đệ quy kể được)  Ô tô mát tuyến tính giới nội  Văn phạm cảm ngữ cảnh
Máy turing tiền định  Cấu tạo:  Bộ chữ gồm: bộ chữ vào (dùng cho xâu vào) và kí hiệu trống B  Một hoặc một số băng chia thành nhiều ô(có đánh số thứ tự) vô hạn về một phía hoặc hai phía. Mỗi ô trên băng có thể chứa được một kí hiệu thuộc bộ chữ  Một đầu đọc di chuyển trên băng, mỗi thời điểm trỏ đến một ô trên băng  Một tập hữu hạn các trạng thái trong đó có trạng thái đầu và trạng thái thừa nhận
Cấu tạo …  Một hàm dịch chuyển với mỗi trạng thái hiện tại và kí hiệu đầu đọc đọc được :  Trạng thái tiếp theo  Một kí hiệu mới đè lên kí hiệu vừa đọc được  Hướng dịch chuyển của đầu đọc
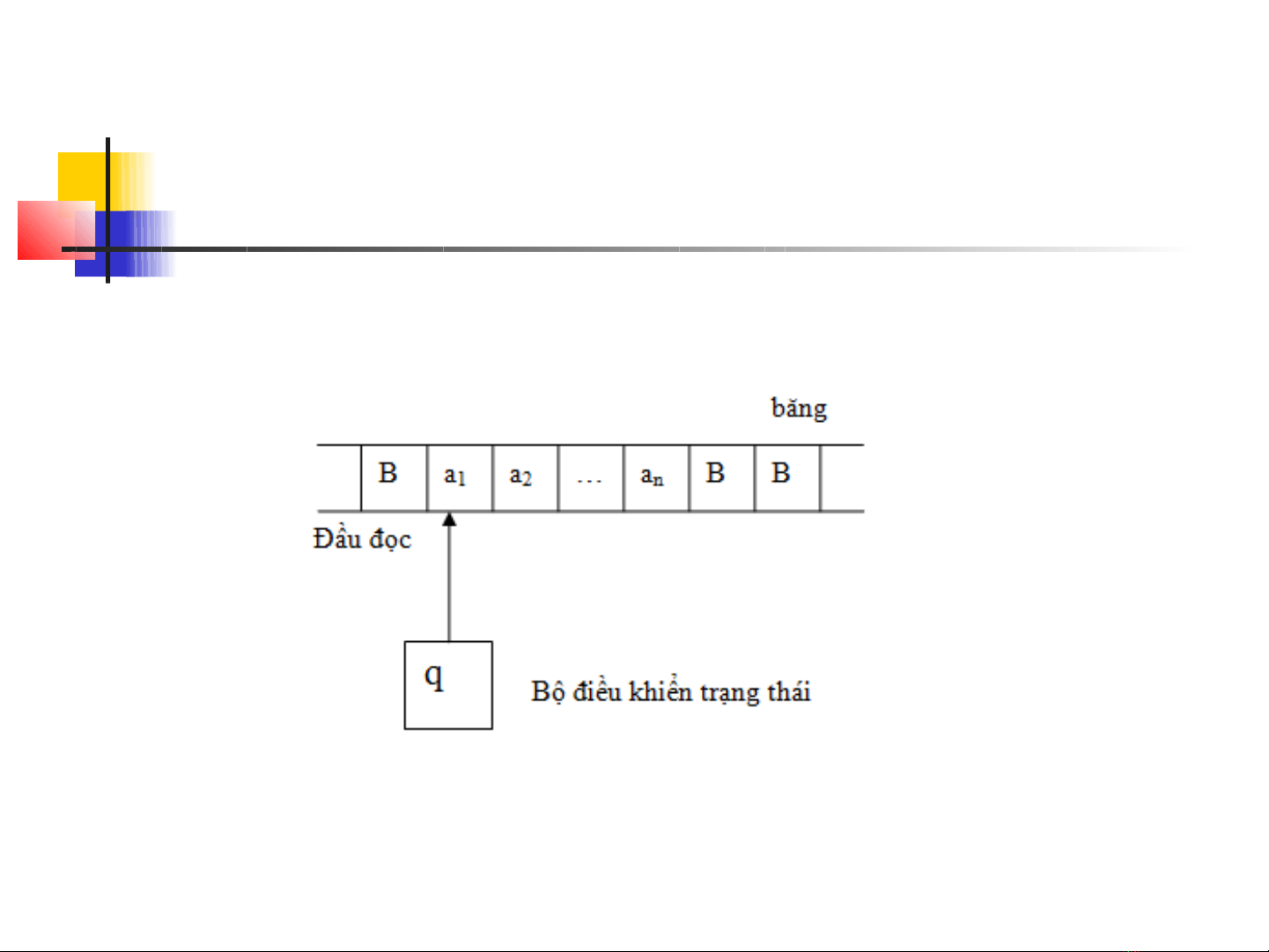
Cấu tạo máy Turing…  Mô hình máy Turing:
Máy turing tiền định  Nguyên lý hoạt động:  Ban đầu:  Xâu được đặt trên băng bắt đầu từ ô đầu tiên, mỗi ô một kí hiệu, các ô khác chứa kí hiệu trắng  Đầu đọc trỏ vào ô đầu tiên trên băng  Trạng thái bắt đầu q 0
Nguyên lý hoạt động  Hàm dịch chuyển căn cứ vào trạng thái hiện tại và kí hiệu đọc được trên băng để xác định:  Trạng thái tiếp theo  Một kí hiệu được viết lên băng (đè lên kí hiệu vừa đọc)  Hướng dịch chuyển của đầu đọc (dịch sang trái hay sang phải một ô)  Xâu vào được thừa nhận khi quá trình thực hiện đối với xâu đạt đến một trạng thái thưà nhận
Định nghĩa máy Turing  Định nghĩa: Một máy Turing là một bộ 7 M=( , Q, , , q0, B, F) trong đó:  Q : tập hữu hạn các trạng thái  Σ : bộ ký hiệu nhập  Γ : tập hữu hạn các ký hiệu được viết trên băng  δ : hàm chuyển Q x Γ → Q x Γ x {L, R, Ø}  q0 : trạng thái khởi đầu  B : ký hiệu dùng để chỉ khoảng trống trên băng  F Q : tập các trạng thái kết thúc
Định nghĩa máy Turing…  Một hình trạng của một máy Turing: # 1q 2# trong đó:  # , # được gọi là kí hiệu mút  q là trạng thái hiện tại  Nội dung trên băng: 1 và 2
Định nghĩa máy Turing  Sự thực hiện của máy turing: 2 trường hợp  Sự thực hiện đến một hình trạng không thể đi tiếp. Máy turing cho câu trả lời “có” (xâu w được thừa nhận) nếu trạng thái hiện thời là trạng thái thừa nhân, ngược lại thì câu trả lời là “không”  Sự thực hiện không kết thúc. Xâu w không được thừa nhận
Định nghĩa máy Turing …  Hệ viết lại ngầm định của máy Turing M: WM=(V, P) Trong đó:  V= Q {#}  P là các quy tắc được lập dựa vào hàm dịch chuyển
Định nghĩa máy Turing…  Cách xây dựng các quy tắc trong P:  Nếu (q,X)=(p,Y,R) thì P có quy tắc:  qXZYpZ với mọi Z (dịch phải)  qX#YpB# (dịch phải sang ô chứa kí hiệu trống)  Nếu (q,X)=(p,Y,L) thì P có quy tắc:  ZqXpZY với mọi Z (dịch trái)
Định nghĩa máy Turing…  Ngôn ngữ thừa nhận (đoán nhận) bởi máy Turing M: L(M)={w *|#q0w#=>*# 1p 2# trong đó 1, 2 * và p F}  Các ngôn ngữ được thừa nhận bởi các máy Turing được gọi là các ngôn ngữ đệ quy kể được  Ngôn ngữ được quyết định bởi máy Turing M nếu:  M thừa nhận L và  M không có các thực hiện vô hạn
Ví dụ về máy Turing  Ví dụ: Máy Turing M chấp nhận L = {0n1n | n > 0} M(Q, Σ, Γ, δ, q0, B, F) trong đó:  Σ={0, 1}  Q = {q0, q1, q2, q3, q4}  Γ = {0, 1, X, Y, B}  F = {q4}
Ví dụ…  Hàm dịch chuyển được xác định như sau: Xét chuỗi 0011 ta có: q00011 => Xq1011 => X0q111 => X q2 0Y1 => q2 X0Y1 => X q0 0Y1 => XXq1Y1 => XXY q1 1 => XX q2 YY => X q2 XYY => XX q YY => XXYq Y => XXYYq => XXYYq (được thừa nhận)
Các ngôn ngữ đệ quy kể đươc, đệ quy(ngữ cấu)  Ngôn ngữ đệ quy kể được là ngôn ngữ được thừa nhận bởi một máy Turing  Ngôn ngữ đệ quy là ngôn ngữ được quyết định bởi một máy Turing
Ngôn ngữ tính toán bởi máy Turing  Cho một máy Turing M, M ngừng với xâu vào u thì xâu còn lại trên băng là fM(u)  Ta gọi ngôn ngữ tính toán bởi M là tập các xâu: {w| Ǝ u sao cho M ngừng với u và w=fM(u)} Định lý V.4: Một ngôn ngữ là ngôn ngữ tính toán bởi một máy Turing khi và chỉ khi nó là ngôn ngữ đệ quy kể được.
Ngôn ngữ sản sinh từ văn phạm loại 0  Văn phạm loại 0 (văn phạm tổng quát): gồm các quy tắc có dạng:  β, β ( )*, ( )* ( )*  Định lý V.5: Một ngôn ngữ là sản sinh từ văn phạm loại 0 khi và chỉ khi nó là ngôn ngữ đệ quy kể được
Tính chất ngôn ngữ đệ quy kể được và đệ quy  Định lý V.6: Nếu L1 và L2 là các ngôn ngữ đệ quy kể được thì L1 L2, L1.L2, L1* là các ngôn ngữ đệ quy kể được  Định lý V.7: Nếu L1 và L2 là các ngôn ngữ đệ quy kể được thì L1 L2 cũng là ngôn ngữ đệ quy kể được  Định lý V.8: Các ngôn ngữ đệ quy kể được là không đóng đối với phép lấy bổ sung
Ngôn ngữ cảm ngữ cảnh  Văn phạm cảm ngữ cảnh: là văn phạm trong đó các sản xuất có dạng: Aβ wβ với ,β ( )*, A , w ( )+  Ngôn ngữ cảm ngữ cảnh là ngôn ngữ được sinh ra bởi văn phạm cảm ngữ cảnh