CHƯƠNG 5.
CHƯƠNG 5.
CÂN BẰNG MÁY
CÂN BẰNG MÁY
NGUYÊN LÝ MÁY
NGUYÊN LÝ MÁY
ĐẠI HỌC CÔNG NGHIỆP TP.HỒ CHÍ MINH
ĐẠI HỌC CÔNG NGHIỆP TP.HỒ CHÍ MINH
KHOA CO KHÍ
KHOA CO KHÍ
§1. Đại cương
§1. Đại cương
I. M c đích cân b ng máyụ ằ
- Khi c c u và máy làm vi c, luôn xu t hi n l c quán tínhơ ấ ệ ấ ệ ự
- L c quán tính thay đ i theo chu kỳ làm vi c c a máy và ph thu c v trí c a c ự ổ ệ ủ ụ ộ ị ủ ơ
c u ấ áp l c trên các kh p ph thu c vào l c quán tính và thay đ i có chu kỳự ớ ụ ộ ự ổ
- Áp l c này đ c g i là ph n l c đ ng ph (phân bi t v i áp l c không đ i do ự ượ ọ ả ự ộ ụ ệ ớ ự ổ
t i tr ng tĩnh gây nên)ả ọ
- Vì bi n thiên có chu kỳ nên l c quán tính là nguyên nhân ch y u gây ra hi n ế ự ủ ế ệ
t ng rung đ ng trên máy và móng máy ượ ộ làm gi m đ chính xác c a máy và ả ộ ủ
nh h ng đ n các máy xung quanh, n u c ng h ng có th phá h y máyả ưở ế ế ộ ưở ể ủ
Ph i kh l c quán tính, l ai tr ngu n g c gây nên rung đ ngả ử ự ọ ừ ồ ố ộ
Đây là m c đích c a vi c cân b ng máyụ ủ ệ ằ
§1. Đại cương
§1. Đại cương
II. N i dung cân b ng máyộ ằ
- Cân b ng v t quayằ ậ – phân ph i l i ố ạ kh i l ng v t quayố ượ ậ đ kh l c quán tính ể ử ự
ly tâm và moment quán tính c a cac v t quayủ ậ
- Cân b ng c c uằ ơ ấ – phân ph i l i ố ạ kh i l ng các khâuố ượ trong c c u đ khi c ơ ấ ể ơ
c u làm vi c, t ng các l c quán tính trên tòan b c c u tri t tiêu và không t o ấ ệ ổ ự ộ ơ ấ ệ ạ
nên áp l c đ ng trên n nự ộ ề
§2. Cân bằng vật quay
§2. Cân bằng vật quay
I. Các tr ng thái cân b ng c a v t quayạ ằ ủ ậ
Ba tr ng thái m t cân b ng c a v t quayạ ấ ằ ủ ậ
- M t cân b ng tĩnhấ ằ
- M t cân b ng đ ng thu n túyấ ằ ộ ầ
- M t cân b ng đ ng h n h p (m t cân b ng đ ng)ấ ằ ộ ỗ ợ ấ ằ ộ
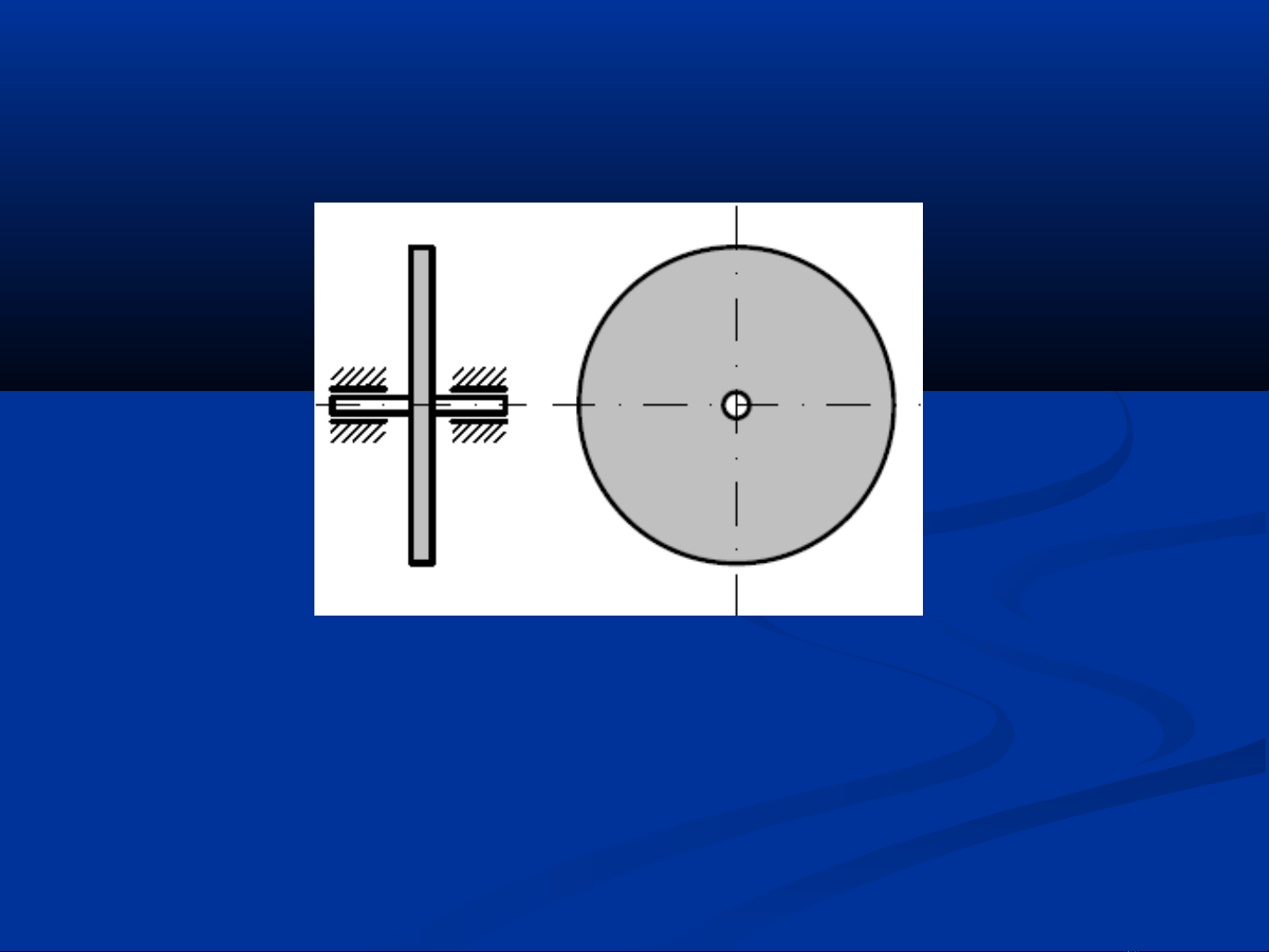
§2. Cân bằng vật quay
§2. Cân bằng vật quay
I. Các tr ng thái cân b ng c a v t quayạ ằ ủ ậ
1. M t cân b ng tĩnhấ ằ
- Xét m t dĩa tròn kh i l ng có tr c quay đi qua tr ng tâm dĩa và vuông góc ộ ố ượ ụ ọ
v i m t dĩa. Khi cho dĩa quay quanh tr c, các ph n t trên dĩa gây ra nh ng l c ớ ặ ụ ầ ử ữ ự
quán tính hòan tòan cân b ng nhau, không có l c tác d ng lên tr c ng ai tr ằ ự ụ ụ ọ ừ
b n than tr ng l ng dĩa ả ọ ượ Ta nói dĩa đ c cân b ng tĩnhượ ằ