Chương 5: Thanh Chịu Xoắn –Chịu Cắt
1Giới Thiệu
2Nội Lực Trên Mặt Cắt Ngang
3Ứng Suất Trên Mặt Cắt Ngang
5Ứng Suất Trượt Thuần Túy
6Điều Kiện Bền, Điều Kiện Cứng
7Thế Năng Biến Dạng Đàn Hồi
4Biến Dạng
8Hệ Siêu Tĩnh
9Thanh Chịu Cắt
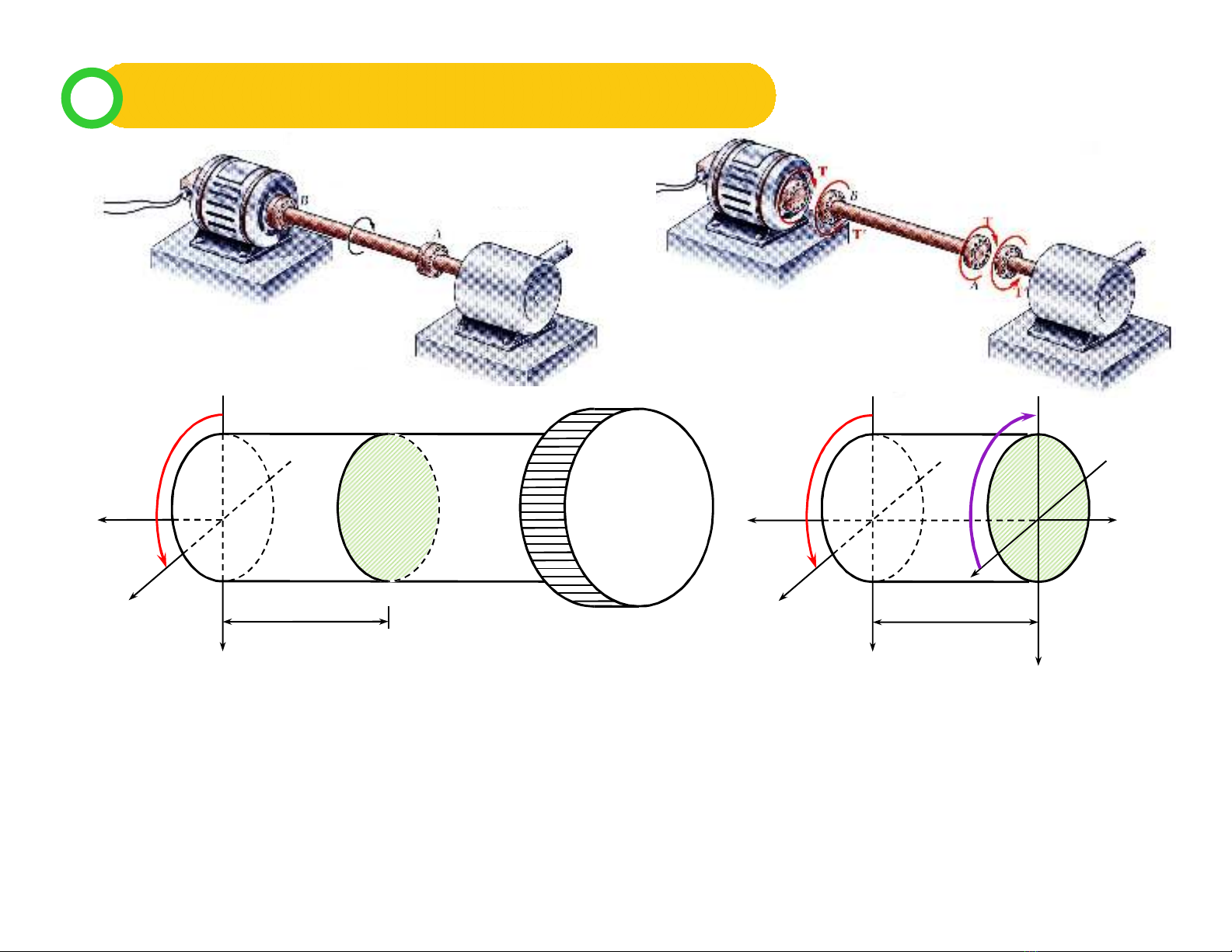
*Thanh chỉ chịu tác dụng của ngẫu lực tập trung hay ngẫu lực phân bố
quay quanh trục thanh.
*Một thanh chịu xoắn thuần túy khi trên mặt cắt ngang của thanh chỉ tồn tại
duy nhất một thành phần nội lực:
z
M
1Giới Thiệu
1
z
y
x
z
M
1
z
y
x
z
M
z
y
x
z
M
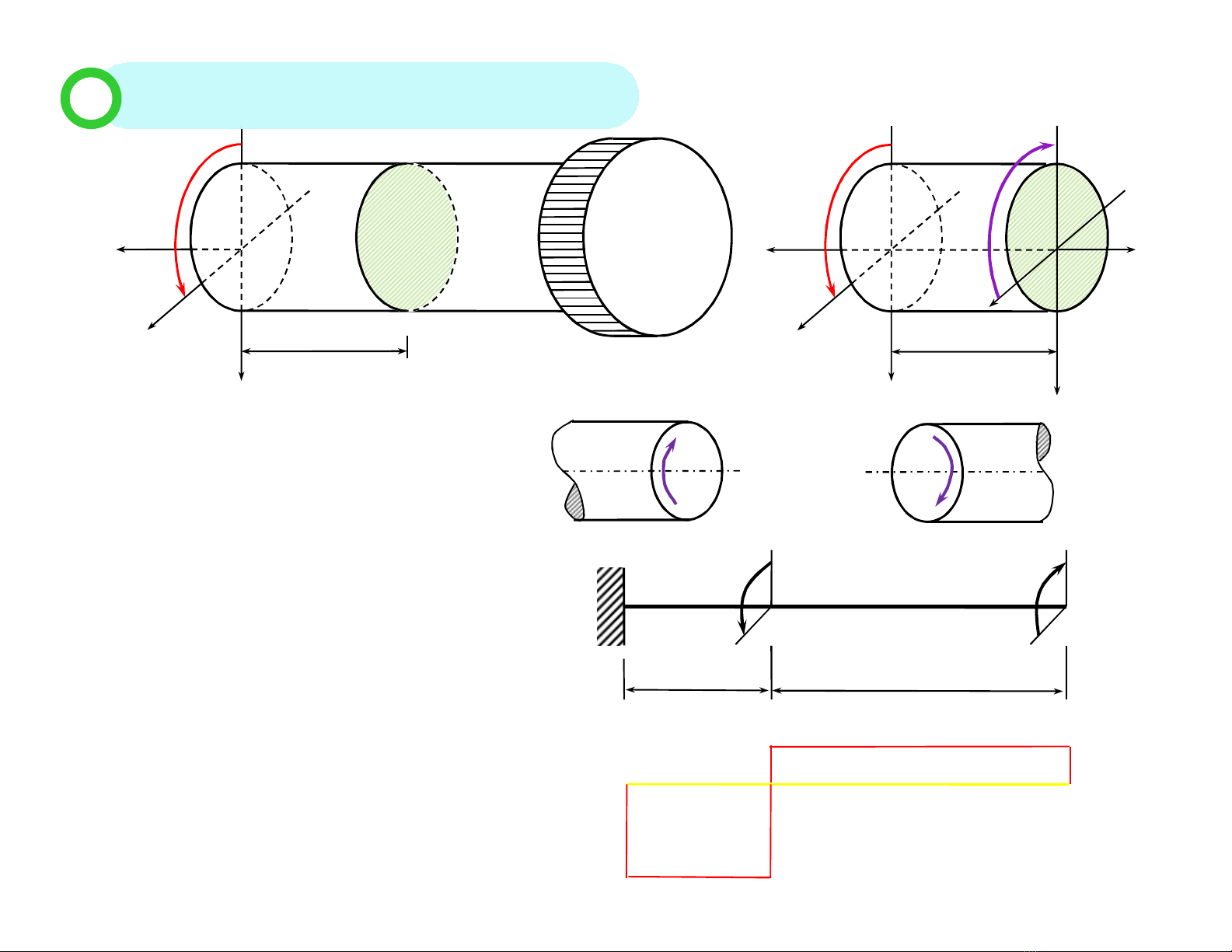
*Qui ước dấu của:
z
1
z
y
x
z
M
1
z
y
x
z
M
z
y
x
z
M
2Nội Lực Trên Mặt Cắt Ngang
*Tồn tại duy nhất
z
M
0
z
M
*Biểu đồ nội lực:
M
2
a
4
M
A
B
C
a
M
3
M
z
M
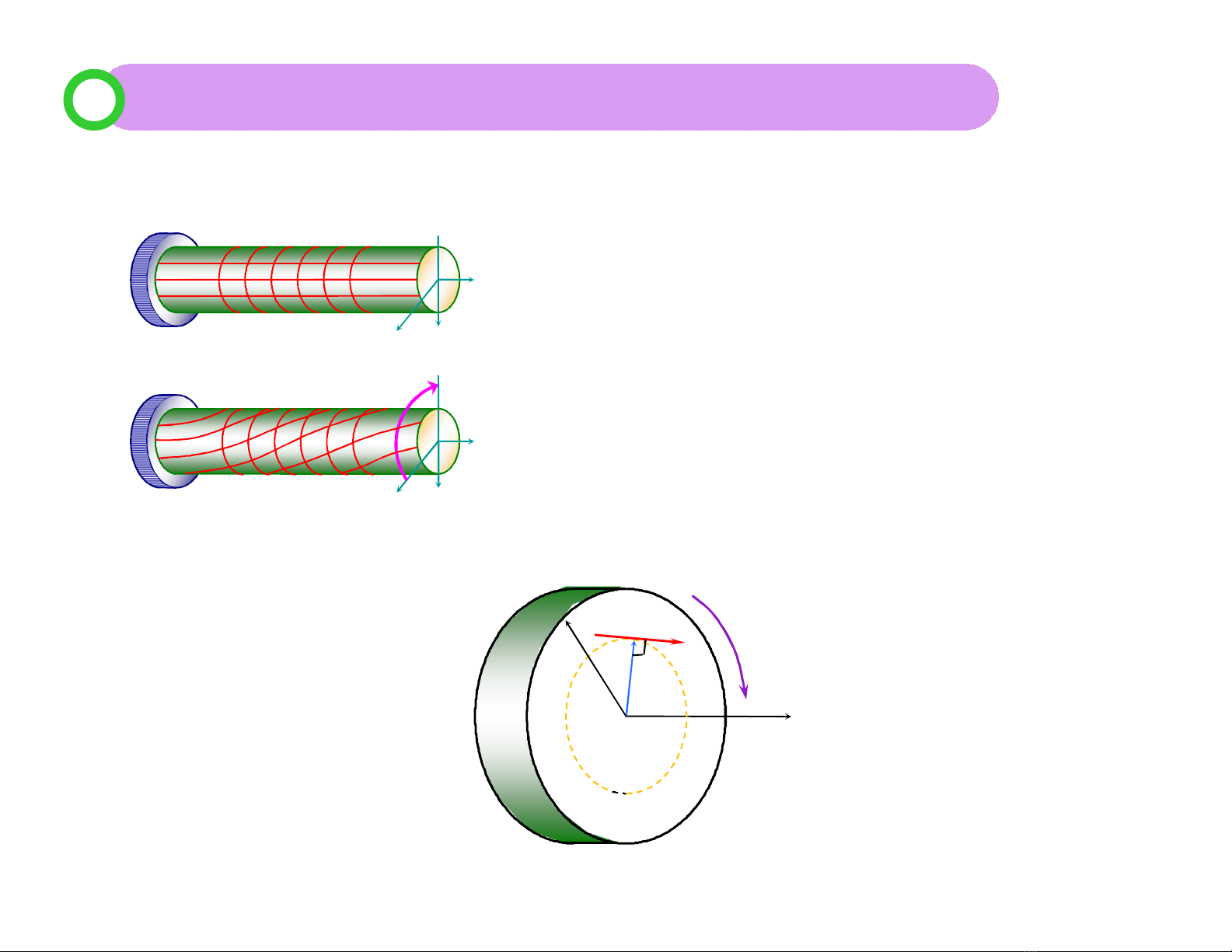
*Mặt cắt ngang phẳng, thanh không có
biến dạng dài dọc trục, bán kính mặt cắt
ngang vẫn thẳng và có chiều dài không đổi
0
x y z
3.1 Các giả thiết về biến dạng:
3Ứng Suất Trên Mặt Cắt Ngang Của Thanh Chịu Xoắn
y
x
z
y
x
z
M
*Góc vuông thay đổi nên tồn tại ứng suất
tiếp trên mặt cắt và vuông góc với bán kính.
Z
M
O
R
Z
Hình 5.2
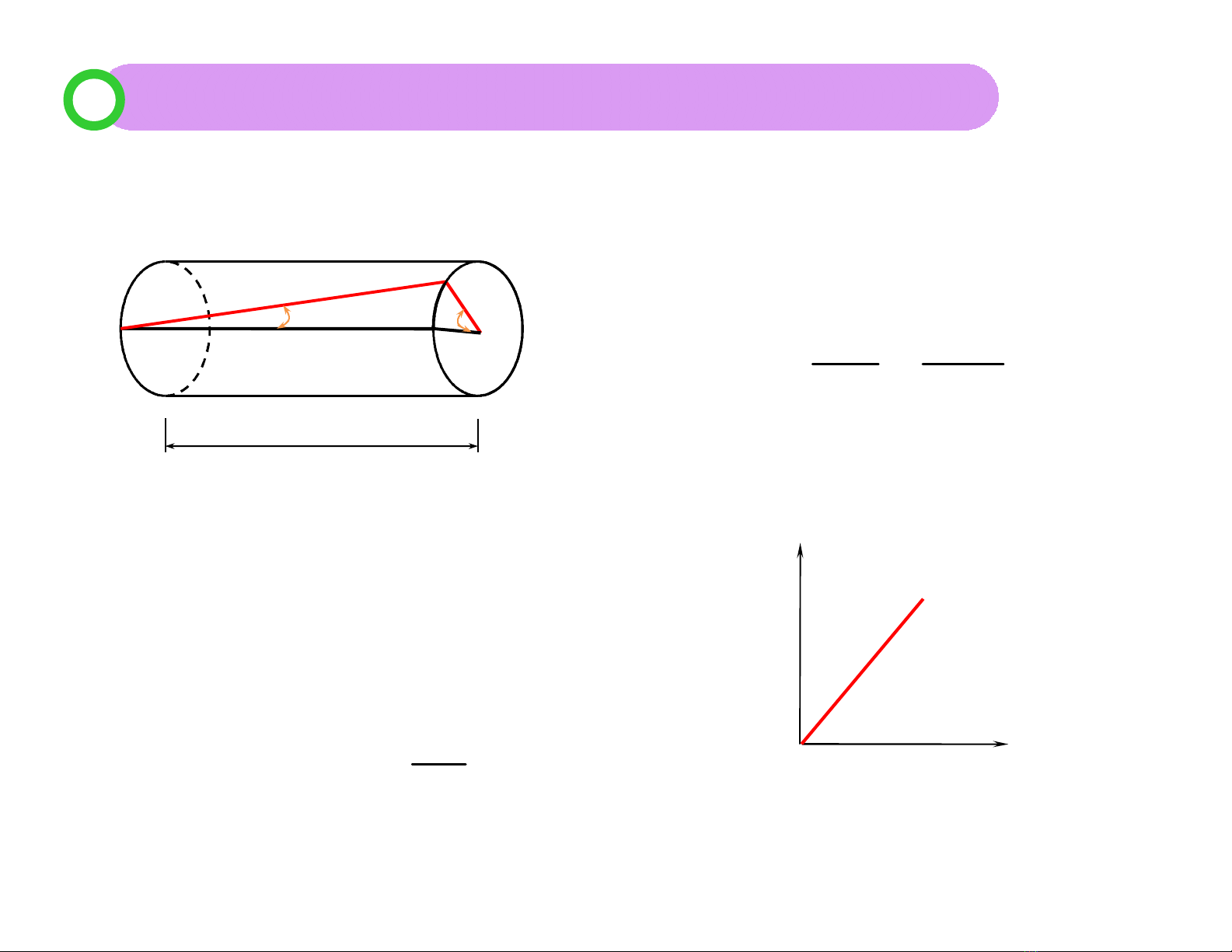
*Vì biến dạng bé nên:
'
BB d
tg
AB dz
3.2 Biểu thức tính ứng suất trên mặt cắt ngang của thanh tròn chịu xoắn:
3Ứng Suất Trên Mặt Cắt Ngang Của Thanh Chịu Xoắn
d
A
B
'
B
O
dz
*Theo định luật Hooke:
G
zz E
G: mô đun trượt của vật liệu
(1)
d
G
dz