zunia.vn

Tuyển sinh 2024 dành cho Gen-Z

zunia.vn

» Kỹ Thuật - Công Nghệ

» Cơ khí - Chế tạo máy

Bài giảng Thiết kế nguyên lý máy: Chương 2 - TS. Nguyễn Bá Hưng

Chia sẻ: _ _ | Ngày: | Loại File: PDF | Số trang:45

Báo xấu

6
lượt xem 2
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng Thiết kế nguyên lý máy - Chương 2: Phân tích và tổng hợp động học cơ cấu phẳng toàn khớp thấp, được biên soạn gồm các nội dung chính sau: Phân tích động học cơ cấu phẳng toàn khớp thấp; Tổng hợp cơ cấu 4 khâu phẳng. Mời các bạn cùng tham khảo!

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Thiết kế nguyên lý máy: Chương 2 - TS. Nguyễn Bá Hưng

Đại học Bách Khoa Hà Nội Viện Cơ khí Bộ môn Cơ sở thiết kế máy và Robot Bài giảng Phân tích và tổng hợp động học cơ cấu phẳng toàn khớp thấp Giảng viên: TS. Nguyễn Bá Hưng
Nội dung  Phân tích động học cơ cấu phẳng toàn khớp thấp  Tổng hợp cơ cấu 4 khâu phẳng
Nội dung  Phân tích động học cơ cấu phẳng toàn khớp thấp  Tổng hợp cơ cấu 4 khâu phẳng
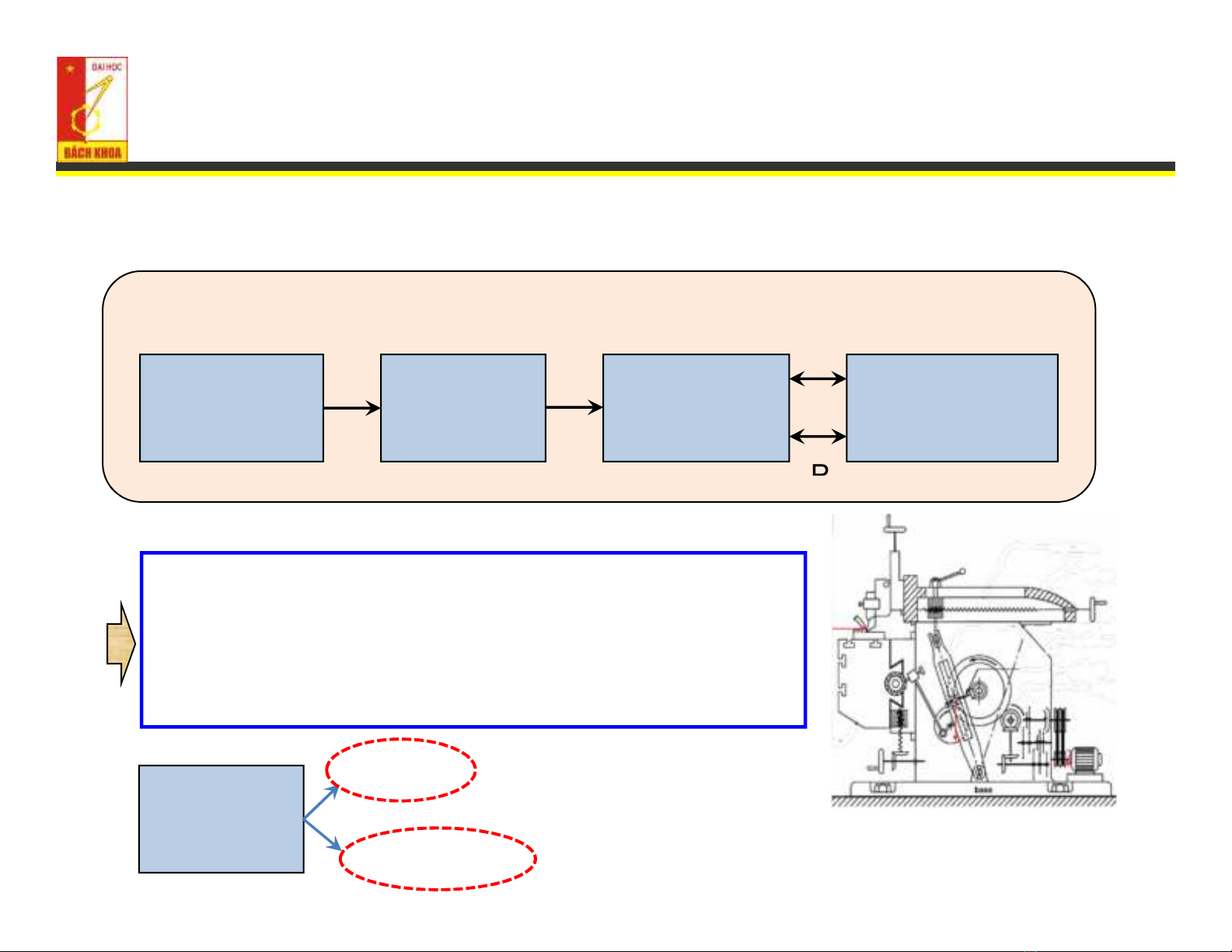
Đặt vấn đề  Tại sao phải phân tích động học cơ cấu ? Mô hình cơ bản của máy x Đối tượng Động cơ Cơ cấu Công tác công nghệ P Phân tích động học để đảm bảo chuyển động của cơ cấu theo đúng yêu cầu công nghệ Phẳng – Không gian Cơ cấu Ví dụ minh họa: máy bào Khớp thấp – khớp cao
Nội dung phân tích động học  Số liệu cho trước:  Lược đồ và kích thước động học của cơ cấu  Quy luật chuyển động của các khâu dẫn  Yêu cầu:  Xác định thông số động học của cơ cấu  Bài toán vị trí  Biến thiên vị trí của các khâu bị dẫn  Quỹ đạo của điểm làm việc  Bài toán vận tốc  Biến thiên vận tốc của các khâu bị dẫn  Vận tốc của điểm làm việc  Bài toán gia tốc Biến thiên gia tốc của các khâu bị dẫn  Gia tốc của điểm làm việc
Phương pháp phân tích động học  Phương pháp giải tích  Phương pháp đồ thị động học  Phương pháp họa đồ véc tơ
Phương pháp phân tích động học  Phương pháp giải tích  Phương pháp đồ thị động học  Phương pháp họa đồ véc tơ
Phương pháp giải tích  Cơ sở lý thuyết  Bài toán vị trí  Phương trình véc tơ của lược đồ động cơ cấu 4 khâu phẳng 4 l i 1 i 0 (*) Nếu gọi véc tơ ei và li lần lượt là véc tơ đơn vị chỉ phương và chiều dài của véc tơ li Phương trình (*) được viết lại : l2 4 e2  li ei  0 i 1 e1 l1 e3 l3 l4 e4
Phương pháp giải tích  Cơ sở lý thuyết  Bài toán vị trí  Phương trình hình chiếu của lược đồ động  y l2 3 4 4 e2  e3  li ei e 0  0  li cos i  0 l1 2  i 1  i 1 4 4 e1 1  l ei n 0  0  i l3  l sin   0  i n e x 0  i  l4 4  i 1  i 1 x e4 e0 0 x e0 n ev e , e      v u v u e ,e        0  v eu  v u v u  e , e        u e0 v u v u
Phương pháp giải tích  Cơ sở lý thuyết  Bài toán vận tốc  Đạo hàm theo t phương trình véc tơ lược đồ động: 3  d 3  dli d ei    li ei    dt ei  li dt   0 dt i 1 1   (**)   dli  Đặt:  li dt d ei di Chú ý:  n i  i n i dt dt Phương trình (**) được viết lại :  l e  3 i i  i li n i  0 1
Phương pháp giải tích  Cơ sở lý thuyết  Bài toán vận tốc  Các phương trình hình chiếu vận tốc: 3  1 l e   l n e i i i i i 0 0 3   l e   l n n i i i i i 0 0 1 3  l cos    l sin   0 i i i i i 1 3   l sin    l cos   0 i i i i i 1
Phương pháp giải tích  Cơ sở lý thuyết  Bài toán gia tốc  Đạo hàm theo t phương trình véc tơ vận tốc: d 3     li ei  ili ni  0 dt 1 (***) Đặt: d   d l  i  i ; li i dt dt d ni Ngoài ra:  i ei dt  i2li e i là véc tơ gia tốc pháp tuyến hướng tâm Phương trình (***) được viết lại :  i li n i là véc tơ gia tốc tiếp tuyến    l e   l n  2 l n  e  0 3 2i li n i là véc tơ gia tốc Cô-ri-ô-lít 2 i i i i i i li i i i i  ei li là véc tơ gia tốc tương đối giữa hai điểm khác khâu và hiện trùng 1 với nhau
Phương pháp giải tích  Cơ sở lý thuyết  Bài toán gia tốc  Phương trình hình chiếu của gia tốc: 3  1    i2li ei   i li n i  2i li n i   ei e 0  0 li 3 1  i i i i li     2l ei   l n i  2 l n i   ei n 0  0  ii  3     i2li cos i   i li sin i  2i li sin i   cos i  0 li 1 3 1     2l sin    l cos   2 l cos    sin   0  i i i ii i i i i li i 
Phương pháp giải tích  Ví dụ minh họa  Cơ cấu tay quay con trượt - bài toán vị trí 4 y l1  2 l i 1 i 0 e1 1 e2 l2 l4   3 l1  l 2  l 3  l 4  0 4 e4 n 0 l3 e3 l 3  l 1  l 2  l 4 0 e0 x l 3 e 3  l 1 e 3  l 2 e 3  l 4 e 3  l3  l1 cos(1  3 )  l2 cos( 2   3 ) (a)   l 3 e 4  l 1 e 4  l 2 e 4  l 4 e 4  0  l1 cos(1   4 )  l2 cos( 2   4 )  l4 (b) l3 e 3 e 3  l1 e1 e 3  l2 e 2 e 3  l4 e 4 e 3 Từ (b)   l1 cos(1   4 )  l4    2   4  arccos      l2  l3 e 3 e 4  l1 e1 e 4  l2 e 2 e 4  l4 e 4 e 4  Thay 2 vào (a) tính được l3
Phương pháp giải tích  Ví dụ minh họa  Cơ cấu tay quay con trượt - bài toán vân tốc y  2 3  l cos   l sin   0 i i i i i l1 1 3 l4 e1 1 e2 l2    l sin    l cos  0 i i i i i  3 1 4 n 0 e4 l3 e3 l3 cos 3   2l2 sin  2  1l1 sin 1   l3 sin 3  2l2 cos  2  1l1 cos 1  0 e0 x cos  3  l2 sin  2  0  l3  1 sin  3 l2 cos  2 0 1l1 sin 1  l2 sin  2 Với: 1  2  1l1 cos 1 l2 cos  2 2  0 cos  3 1l1 sin 1 2  sin  3  1l1 cos 1
Phương pháp giải tích  Ví dụ minh họa  Cơ cấu tay quay con trượt - bài toán gia tốc y  2 3  2      i li cos i   i li sin i  2i li sin i  li cos i  0 1 l1 3 e1 1 e2 l2     2l sin    l cos   2 l cos    sin   0  i i i i i i i i i li  i 1 l4   4 3 n 0 e4  2l2 sin  2   cos  3  b1  l3 l3 e3   2l2 cos  2   sin  3  b2  l3 0 b1  1 l1 cos 1  2 l2 cos  2   1l1 sin 1  2 2 e0 x Với:  b2  12l1 sin 1  2 l2 sin  2  1l1 cos 1  2 l2 sin  2  cos  3  0  2  1 l2 cos  2 sin  3 0 b1  cos  3 Với: 1  b2 sin  3    2 l3 0 l2 sin  2 b1 2  l2 cos  2 b2
Phương pháp phân tích động học  Phương pháp giải tích  Phương pháp đồ thị động học  Phương pháp họa đồ véc tơ
Phương pháp đồ thị động học  Bài tính vị trí và quỹ đạo  Dữ kiện  Lược đồ động của cơ cấu và khâu dẫn  Yêu cầu  Xác định quy luật chuyển vị của khâu bị dẫn theo khâu dẫn (S=S())  Xây dựng quỹ đạo của điểm bất kỳ trên cơ cấu (điểm M)  Xác định S=S()  Dựng vòng tròn tâm A, bán kính lAB. Chia vòng tròn này thành B1, B2,…, Bn  i=BiAB0  Ci là giao điểm giữa BiCi và AC0  C0Ci là đoạn biểu diễn của chuyển vị con trượt tương ứng i  Chuyển vị thực Si=l.C0Ci  Biểu diễn các cặp giá trị (i,Si) trên hệ tọa độ SO với các tỉ lệ xích  và S => đồ thị chuyển vị S=S()  Xây dựng quỹ đạo điểm M  Gọi Mi là điểm xác định trên thanh truyền BiCi  Nối các điểm Mi ứng với mỗi góc quay i ta được quỹ đạo của điểm M => Đường cong thanh truyền
Phương pháp đồ thị động học  Bài tính vận tốc, gia tốc  Sau khi đã xác định được quan hệ giữa chuyển vị của các khâu và tọa độ của các điểm với góc quay của khâu dẫn là những quan hệ hàm số: Đạo hàm Đạo hàm Vị trí Vận tốc Gia tốc 1  1 t   S  S 1   xM  xM 1    yM  yM 1 
Phương pháp đồ thị động học  Bài tính vận tốc Đạo hàm Đạo hàm Vị trí Vận tốc Gia tốc 1  1 t   S  S 1  dS dS d1 dS v  .  1. dt d1 dt d1  xM  xM 1    yM  yM 1   dx dx d dx v xM  M  M . 1  1. M  dt d1 dt d1  v  dyM  dyM . d1   . dyM  yM  dt d1 dt 1 d1

CÓ THỂ BẠN MUỐN DOWNLOAD

LV.15: Bộ Đồ Án Tốt Nghiệp Chuyên Ngành Cơ Khí

65 tài liệu

2431 lượt tải

THÔNG TIN

TRỢ GIÚP

HỖ TRỢ KHÁCH HÀNG

Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.